CHIMIE

Partie I : Etude de l'acide formique

1- Solution aqueuse de chlorure d'ammonium

1-1- Équation de la réaction :

$$\mathrm{NH}_{(\mathrm{aq})}^{+4}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{NH}_{3(\mathrm{aq})}+\mathrm{H}_3 \mathrm{O}_{(\mathrm{aq})}^{+}\\[0.5cm]$$

1-2- Expression de $\tau$ :

On a : $~~\lambda=\lambda_1 \times\left[\mathrm{H}_3 \mathrm{O}^{+}\right]+\lambda_2 \times\left[\mathrm{NH}_4^{+}\right]+\lambda_3 \times[\mathrm{Cl}^-]$

Avec $:~~\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\frac{x f}{\mathrm{~V}}$

$\left[\mathrm{NH}_4^{+}\right]=\frac{\mathrm{C} \cdot \mathrm{V}-x f}{\mathrm{~V}}=\frac{x f}{\mathrm{~V}}=\mathrm{C}-\left[\mathrm{H}_3 \mathrm{O}^{+}\right]$

$[\mathrm{Cl}^-]=\mathrm{C}$

D'où : $~~\sigma=\lambda_1 \times\left[\mathrm{H}_3 \mathrm{O}^{+}\right]+\lambda_2 \times\left(\mathrm{C}-\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\right)+\lambda_3 \times \mathrm{C}$

$$\Rightarrow \sigma=\left(\lambda_1-\lambda_2\right) \times\left[H_3 \mathrm{O}^{+}\right]+\left(\lambda_2+\lambda_3\right) \times \mathrm{C}$$

Donc : $~~\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\frac{\sigma-\left(\lambda_2+\lambda_3\right) \times \mathrm{C}}{\lambda_1-\lambda_2}$

On sait que : $~~\tau=\frac{x f}{x_{\max }}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \times \mathrm{V}}{\mathrm{C} \times \mathrm{V}}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{\mathrm{C}}$

D'où : $~~\tau=\frac{\sigma-\left(\lambda_2+\lambda_3\right) \times C}{C\left(\lambda_1-\lambda_2\right)}$

Application numérique :

$$\begin{aligned} \tau &=\frac{74,898 \times 10^{-3}-(7,34+7,63) \times 10^{-3} \times 5}{5 \times(34,9-7,34) \times 10^{-3}}\\ &=3,48 \times 10^{-4} \end{aligned}$$

$\tau \approx 0,035 \% .\\[0.5cm]$

1-3- Expression de $\mathrm{K}_{\mathrm{A}}$ :

On sait que $~~\mathrm{K}_{\mathrm{A}}=\frac{\left[\mathrm{NH}_3\right] \times\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{\left[\mathrm{NH}_4^{+}\right]}=\frac{\left[\mathrm{H}_3\mathrm{O}^{+}\right]^2}{\mathrm{C}-\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}$

Soit : $~~\mathrm{K_A=\frac{(C \times \tau)^2}{C-\tau \times \tau}=\frac{C \times \tau^2}{1-\tau}}$

A.N : $~~\mathrm{K}_{\mathrm{A}}=\frac{5 \times 10^{-3} \times\left(3,5 \times 10^{-4}\right)^2}{1-3,5 \times 10^{-4}}=6,13 \times 10^{-10}$

$\mathrm{pK}_{\mathrm{A}}=-\log \mathrm{K}_{\mathrm{A}}=9,2\\[[0.5cm]$

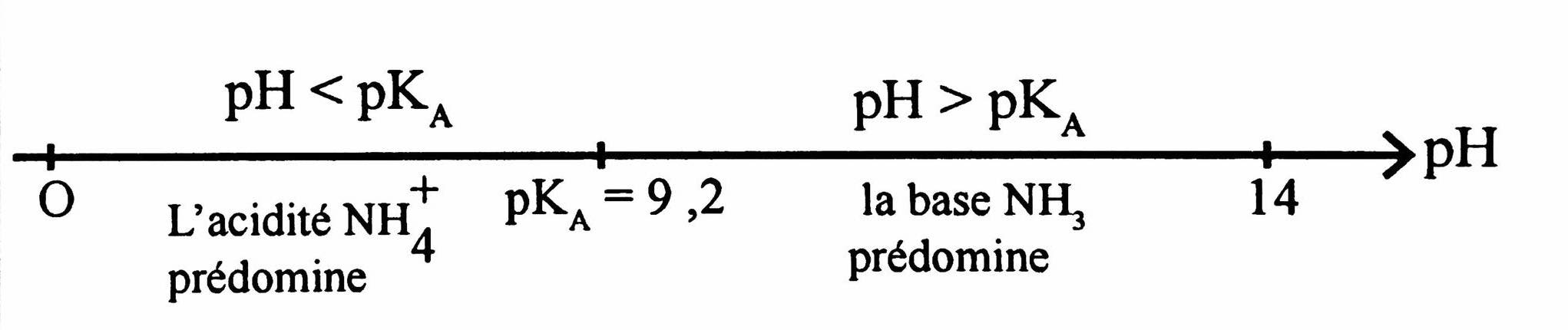
1-4- Diagramme de prédominance :

$$\begin{aligned}\text{On a : } ~~&\mathrm{pH} =-\log \left[\mathrm{H}_3 \mathrm{O}^{+}\right]=-\log (\tau \times \mathrm{C}) \\[0.2cm] &\mathrm{pH} =-\log \left(3,5 \times 10^{-4} \times 5 \times 10^{-3}\right) \approx 5,76 .\end{aligned}$$

Dans cette solution on a : $~\mathrm{pH}<\mathrm{pK}_{\mathrm{A}}~$ donc l'acide $\mathrm{NH}_4^{+}$ prédomine dans cette solution.$\\[0.5cm]$

1-5-Le nombre de propositions justes est 2.$\\[0.5cm]$

2-Dosage acide-base :

2-1-Équation de la réaction :

$$\mathrm{NH}_4^{+}+\mathrm{HO}^{-} \rightarrow \mathrm{NH}_3+\mathrm{H}_2 \mathrm{O}\\[0.5cm]$$

2-2- Constante d'équilibre :

$\mathrm{K}=\frac{\left[\mathrm{NH}_3\right]}{\left[\mathrm{NH}_4^{+}\right] \times\left[\mathrm{HO}^{-}\right]}=\frac{\left[\mathrm{NH}_3\right] \times\left[\mathrm{H_3 O^{+}}\right]}{\left[\mathrm{NH}_4^{+}\right] \times[\mathrm{HO}^-] \times\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}$

$\mathrm{K}=\frac{\mathrm{K}_{\mathrm{A}}}{\mathrm{K}_{\mathrm{e}}}=\frac{6,13 \times 10^{-10}}{10^{-14}}=6,13 \times 10^4.\\[0.5cm]$

2-3-À l'équivalence, on a : $~\mathrm{C}_{\mathrm{A}} \times \mathrm{V}_{\mathrm{A}}=\mathrm{C}_{\mathrm{B}} \times \mathrm{V}_{\mathrm{BE}}$

soit: $~~\mathrm{C}_{\mathrm{A}}=\frac{\mathrm{C}_{\mathrm{B}} \times \mathrm{V}_{\mathrm{BE}}}{\mathrm{V}_{\mathrm{A}}}$

Donc : $~~\mathrm{C}_{\mathrm{A}}=\frac{2 \times 10^{-2} \times 28,3}{20}=2,83 \times 10^{-2} \mathrm{~mol} . \mathrm{L}^{-1}$

On a la relation: $~~\mathrm{C}_0=\mathrm{C}_{\mathrm{A}} \times \mathrm{M}$

Soit : $~~\mathrm{C}_0=2,83 \times 10^{-2} \times 53,5 \approx 1,51$ g. $\mathrm{L}^{-1}$

Donc l'indication est correcte.$\\[0.5cm]$

Partie II

1- Équation de la relation :

$$\left(\mathrm{Ag}^{+}+\mathrm{e}^{-} \rightleftharpoons \mathrm{Ag}\right) \times 2$$

$\frac{\mathrm{Ni} \rightleftharpoons \mathrm{Ni}^{2+}+2 \mathrm{e}^{-}}{\mathrm{Ni}_{(\mathrm{s})}+2 \mathrm{Ag}_{(\mathrm{aq})}^{+} \rightleftharpoons \mathrm{Ni}_{(\mathrm{aq})}^{2+}+2 \mathrm{Ag}_{(\mathrm{s})}}\\[0.5cm]$

2- Capacité maximale de la pile :

On a $~~\mathrm{Q}_{\max }=\mathrm{n}(\mathrm{e}-) \times \mathrm{F}=2 x_{\max } \times \mathrm{F}$

Avec $: ~~x_{\max }=n i(\mathrm{Ni})=\frac{\mathrm{m}_0}{\mathrm{M}}=\frac{1,5}{58,7}=2,56 \times 10^{-2} \mathrm{~mol}$

Ou bien $: ~~x_{\max }=\frac{\left[\mathrm{Ag}^{+}\right]_{\mathrm{i}} \times \mathrm{V}}{2}=\frac{0,1 \times 0,1}{2}=5 \times 10^{-3} \mathrm{~mol}$

Donc $: ~~x_{\max }=5 \times 10^{-3} \mathrm{~mol}$

Et $:~~ \mathrm{Q}_{\max }=2 \times 5 \times 10^{-3} \times 9,65 \times 10^4=965 \mathrm{C}.\\[0.5cm]$

3- On a : $~~\mathrm{I \times \Delta t=2 x} \times \mathrm{F}$

Soit : $~~x=\frac{\mathrm{I} \times \Delta \mathrm{t}}{2 \times \mathrm{F}}=\frac{0,2 \times 30 \times 60}{2 \times 9,65 \times 10^4}=1,86 \times 10^{-3} \mathrm{~mol}$

Et : $~~\left[\mathrm{Ni}^{2+}\right]=\left[\mathrm{Ni}^{2+}\right]_{\mathrm{i}}+\frac{x}{\mathrm{~V}}=\frac{0,1+1,86 \times 10^{-3}}{0,1}$

$\left[\mathrm{Ni}^{2+}\right]=1,186 \times 10^{-1} \mathrm{~mol} \cdot \mathrm{L}^{-1} \approx 0,12$ mol. $\mathrm{L}^{-1}$