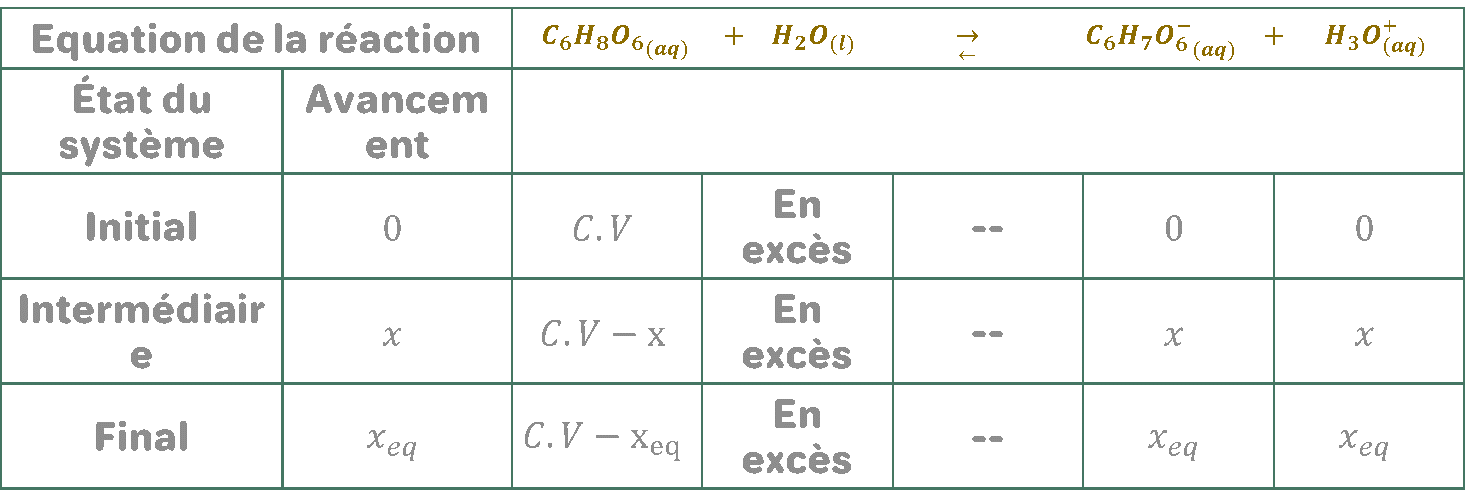Partie 1

1. la valeur de l’avancement maximale $$ \boldsymbol{x}_{\max } $$

On considère que  $$ S_{2} O_{8}^{2-} $$ le réactif limitant:

$$ n_{2}-x_{\max 2}=0 \rightarrow x_{\max 2}=n_{2}=2.10^{-2} \mathrm{~mol}$$

On considère que $$ I^{-} $$ le réactif limitant:

$$ n_{1}-2 x_{\max 1}=0 \rightarrow x_{\max 1}=\frac{n_{1}}{2}=\frac{8.10^{-2}}{2}=4.10^{-2} \mathrm{~mol} $$

Puisque $$ x_{\max 1}>x_{\max 2} $$, l’avancement maximal $$ x_{\max }=2.10^{-2} \mathrm{~mol} $$ et le réactif limitant est $$ S_{2} O_{8}^{2-} $$.

2.1. La vitesse volumique de réaction à l’instant  $$ t_{0}=0 $$. 

L’expression de la vitesse est $$ V(t)=\frac{1}{V}. \frac{d x}{d t} $$ et d’après le tableau d’avancement:

$$ n\left(I_{2}\right)=x \text { donc } \frac{\mathrm{d} n\left(I_{2}\right)}{d t}=\frac{d x}{d t} $$

$$ \begin{array}{c} v(t)=\frac{1}{V} \cdot \frac{d n\left(I_{2}\right)}{d t} \\ v\left(t_{0}\right)=\frac{1}{V} \cdot\left(\frac{\Delta n\left(I_{2}\right)}{d t}\right)_{t_{0}} \rightarrow V\left(t_{0}\right)=\frac{1}{200 \times 10^{-3}} \times \frac{6.10^{-3}}{10,8} \\ \rightarrow V\left(t_{0}\right)=3,85.10^{-3} \mathrm{mol.} L^{-1} \cdot \mathrm{min}^{-1} \end{array} $$

2.2. La concentration des réactifs diminue au cours de la réaction, sachant que la concentration est un facteur cinétique, donc la vitesse volumique diminue au cours du temps.

2.3. En chauffant le milieu réactionnel, la vitesse de la réaction augmente, puisque la température est un facteur cinétique permet d’accélérer la réaction. 

2.4. À $$t=t_{1 / 2} $$ on a :

$$ \begin{array}{c} x\left(t_{1 / 2}\right)=\frac{x_{\max }}{2}=\frac{2.10^{-2}}{2}=10^{-2} \mathrm{~mol} \\ n\left(I_{2}\right)\left(t_{\frac{1}{2}}\right)=x\left(t_{1 / 2}\right)=\frac{x_{\max }}{2}=10.10^{-3} \mathrm{~mol} \end{array} $$

Graphiquement $$ t_{1 / 2}=24 \mathrm{~min} $$

Partie 2

1. Étude d’une solution aqueuse d’acide ascorbique 

1.1. Identifier les deux couples acide/base mis en jeu 

D’après l’équation de la réaction:

$$ C_{6} H_{8} O_{6_{(a q)}}+H_{2} O_{(l)} \underset{\leftarrow}{\rightarrow} C_{6} H_{7} O_{6}^{-}+H_{3} O_{(a q)}^{+} $$

Les deux couples acide/base mis en jeu: 

$$H_{3} O_{(a q)}^{+} / H_{2} O_{(l)} \text { et } C_{6} H_{8} O_{6_{(a q)}} / C_{6} H_{7} O_{6}^{-}(a q)$$

1.2. Dresser le tableau d’avancement de la réaction en utilisant les grandeurs C ,V , l'avancement x et l'avancement $$ \boldsymbol{x}_{\dot{e} q}$$ à l'état d’équilibre du système chimique. 

1.3. Recopier sur votre copie le numéro de la question et écrire la lettre correspondante à la proposition vraie. Le taux d'avancement final de la réaction vaut :

L’expression du taux d’avancement final est $$ \tau=\frac{x_{eq}}{x_{\max }} $$ d’après le tableau d’avancement:

$$ x_{e q}=n_{e q}\left(H_{3} O^{+}\right)=\left[H_{3} O^{+}\right]_{e q} . V $$

Le réactif limitant est l’acide:

$$ \begin{array}{c} C . V-x_{\max }=0 \quad \rightarrow \quad x_{\max }=C . V \\ \tau=\frac{x_{e q}}{x_{\max }}=\frac{\left[H_{3} O^{+}\right]_{e q} \cdot V}{C . V} \rightarrow \tau=\frac{10^{-p H}}{C}=\frac{10^{-3,25}}{4 \cdot 10^{-3}}=0,14 \end{array} $$

1.4. Recopier sur votre copie le numéro de la question et écrire la lettre correspondante à la proposition vraie. Le taux d’avancement final de la transformation dépend :

Le taux d’avancement final $$ \boldsymbol{\tau} $$ dépend de K la constante d’équilibre et de C la concentration initial. 

1.5. Montrer que l'expression de la constante d'équilibre K associée à l'équation de la réaction s'écrit :  $$ K=\frac{C . \tau^{2}}{1-\tau} $$. Calculer la constante d’acidité KA du couple  $$ \mathrm{C}_{6} \mathrm{H}_{\mathrm{8}} \mathrm{O}_{6_{(a q)}} / \mathrm{C}_{6} \mathrm{H}_{7} \mathrm{O}_{6}^{-}(\mathrm{aq}) $$. 

$$ \begin{array}{c} K=\frac{\left[C_{6} H_{7} O_{6}^{-}\right]_{e q} \cdot\left[H_{3} O^{+}\right]_{e q}}{\left[C_{6} H_{8} O_{6}\right]_{e q}} \\ \tau=\frac{\left[H_{3} O^{+}\right]_{e q}}{C} \rightarrow\left[H_{3} O^{+}\right]_{e q}=C . \tau \\ {\left[C_{6} H_{7} O_{6}^{-}\right]_{e q}=\left[H_{3} O^{+}\right]_{e q}=\frac{x_{\varepsilon q}}{V}=C . \tau} \\ {\left[C_{6} H_{8} O_{6}\right]_{e q}=\frac{C . V-x_{\epsilon q}}{V}=C-\frac{x_{e q}}{V}=C-C . \tau=C(1-\tau)} \\ K=\frac{\left[H_{3} O^{+}\right]_{e q}^{2}}{\left[C_{6} H_{8} O_{6}\right]_{e q}}=\frac{C^{2} \cdot \tau^{2}}{C(1-\tau)} \rightarrow K=K_{A}=\frac{C \cdot \tau^{2}}{1-\tau} \\ \rightarrow K_{A}=\frac{4.10^{-3} \times(0,14)^{2}}{1-0,14}=9,12.10^{-5} \end{array} $$

2. Vérification de la masse d’acide ascorbique dans un comprimé 

2.1. Écrire l’équation chimique modélisant la transformation qui a eu lieu lors du dosage. 

$$ C_{6} H_{8} O_{6(a q)}+H O_{(a q)}^{-} \rightarrow C_{6} H_{7} O_{6(a q)}^{-}+H_{2} O_{(l)} $$

2.2. Calculer la concentration molaire $$ C_{A} $$ .

La relation d’équivalence:

$$ \begin{array}{c} C_{A} \cdot V_{A}=C_{B} \cdot V_{B, E} \\ C_{A}=\frac{C_{B} \cdot V_{B, E}}{V_{A}}=\frac{2.10^{-2} \times 14,2 \cdot 10^{-3}}{20.10^{-3}} \\ C_{A}=1,42 \cdot 10^{-2} \text { mol. } L^{-1} \end{array} $$

2.3. En déduire la valeur de la masse d'acide ascorbique contenu dans ce comprimé puis expliquer l'indication «Vitamine C 500». On donne :$$ M\left(C_{6} H_{8} O_{6}\right)=176 \mathrm{g.mol}^{-1} $$.

$$ \begin{array}{c} C_{A}=\frac{n}{V_{0}}=\frac{m}{M \cdot V_{0}} \\ m=C_{A} \cdot V_{0} . M\left(C_{6} H_{8} O_{6}\right)=1,42.10^{-2} \times 200.10^{-3} \times 176=0,4998 g \approx 0,5 g \\ m \approx 500 \mathrm{mg} \end{array} $$

L’indication «Vitamine C 500 » explique la masse d’acide ascorbique est 500 mg dans chaque comprimé.