1. Un acide est toute espèce chimique capable de fournir un ou plusieurs protons au cours d’une réaction chimique.

2. L’équation modélisant la transformation chimique entre l’acide méthanoïque et l’eau :

$\mathrm{HCOOH}_{(a q)}+\mathrm{H}_{3} \mathrm{O}_{(l)} \rightleftarrows \mathrm{HCOO}_{(a q)}^{-}+\mathrm{H}_{3} \mathrm{O}_{(\text {aq })}^{+}$

3. Le tableau d’avancement :

4. La valeur de l’avancement final $\boldsymbol{x}_{f}$de cette réaction :

$\begin{gathered}x_{f}=n_{f}\left(H_{3} O^{+}\right) \\n_{f}\left(H_{3} O^{+}\right)=\left[H_{3} O^{+}\right]_{f} \cdot V=10^{-p H} \cdot V \\x_{f}=10^{-p H} \cdot V \rightarrow \quad x_{f}=10^{-2,4} \times 1=3,98.10^{-3} \mathrm{~mol}\end{gathered}$

5. Le taux d’avancement final $\boldsymbol{\tau}$ de cette réaction :

On a :

$\tau=\frac{x_{f}}{x_{\max }}$

Le réactif limitant est l’acide:

$\begin{gathered}C_{A} \cdot V-x_{\max }=0 \rightarrow x_{\max }=C_{A} \cdot V \\\tau=\frac{x_{f}}{C_{A} \cdot V}=\frac{3,98.10^{-3}}{0,1}=3,98.10^{-2}<1\end{gathered}$

→ la réaction est limitée.

6. Le quotient de réaction à l’état d’équilibre :

$Q_{r, e q}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]_{\mathrm{eq}}\left[\mathrm{HCOO}^{-}\right]_{\mathrm{eq}}}{[\mathrm{HCOOH}]_{\mathrm{e} q}}$

D’après le tableau d’avancement, à l’équilibre:

$\begin{gathered}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]_{\text {éq }}=\left[\mathrm{HCOO}^{-}\right]_{\text {éq }}=x_{f} \cdot V=10^{-p H}} \\{[\mathrm{HCOOH}]_{\text {éq }}=\frac{C_{A} \cdot V-x_{f}}{V}=C_{A}-\frac{x_{f}}{V}=C_{A}-10^{-p H}} \\ Q_{r, e q}=\frac{\left(10^{-p H}\right)^{2}}{C_{A}-10^{-p H}} \rightarrow Q_{r, e q}=\frac{10^{-2 p H}}{C_{A}-10^{-p H}}=\frac{10^{-2 \times 2,4}}{0,1-10^{-2,4}}=1,65.10^{-4}\end{gathered}$

7. La valeur de la constante d’équilibre K associé à l’équation de la réaction :

On a :

$K=D_{r, é q}$

Donc:

$K=1,65.10^{-4}$

Partie 2 – Dosage de la solution aqueuse d’acide méthanoïque

1. Les éléments correspondants aux numéros indiqués sur le montage de la figure.

• pH-mètre
• Solution aqueuse $\left(S_{B}\right)$ d’hydroxyde de sodium.
• Solution aqueuse $\left(S_{A}\right)$ d’acide méthanoïque.

2. L’équation de la réaction qui se produit entre l’acide méthanoïque $\mathrm{HCOOH}_{a q}$ et les ions hydroxydes $\mathrm{HO}_{a q}^{-}$ au cours du dosage

$\mathrm{HCOOH}_{(a q)}+\mathrm{HO}_{(a q)}^{-} \rightleftarrows H C O O_{(a q)}^{-}+\mathrm{H}_{2} \mathrm{O}_{(l)}$

3. La valeur de $C_{A}$ :

La relation d’équivalence:

$C_{A} \cdot V_{A}=C_{B} \cdot V_{B E}$

Alors:

$C_{A}=\frac{C_{B} \cdot V_{B E}}{V_{A}}$ $C_{A}=\frac{0,25 \times 8 \times 10^{-3}}{20.10^{-3}} 0,1 \mathrm{~mol} . L^{-1}$

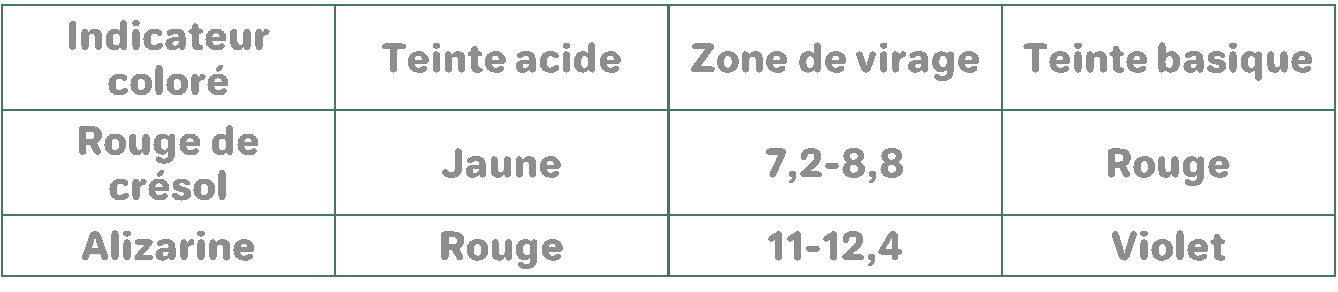
4. Parmi les deux indicateurs colorés suivants, celui qui convient le mieux à ce dosage

L’indicateur qui convient à ce dosage est le rouge de crésol car sa zone de virage contienne la valeur du pH à l’équivalence.

5. La constante d’acidité $\boldsymbol{K}_{A}$ du couple $\left(H C O O H{ }_{a q} / H C O O O_{a q}^{-}\right)$.

La relation qui lie pH et $p K_{A}$

$\begin{gathered} p H=p K_{A}+\log \frac{\left[\mathrm{HCOO}^{-}\right]}{[\mathrm{HCOOH}]} \quad \rightarrow \quad p H=p K_{A}+\log \frac{[\mathrm{HCOOH}]}{[\mathrm{HCOOH}]} \\ p H=p K_{A}+\log 1 \\ p H=p K_{A} \\ K_{A}=10^{-p K_{A}} \\ K_{A}=10^{-3,8} \\ K_{A}=1,58.10^{-4} \end{gathered}$

Partie 3 – Comportement de deux acides en solution aqueuse

1. Plus que l’acide le plus fort (c’est-à-dire le plus dissocié) est celui dont le taux d’avancement final est plus élevé.

$\left\{\begin{aligned} \tau=3,98.10^{-2} &\rightarrow \text { acide méthanoїque } \\ \tau^{\prime}=1,16.10^{-3} &\rightarrow \text { acide propanoїque } \\ \rightarrow \tau &>\tau^{\prime} \end{aligned}\right.$

Conclusion: l’acide méthanoïque se dissocie dans l’eau plus que l’acide propanoïque.

2. L’acide est d’autant plus fort que sa constante d’acidité $K_{A}$ est plus grande.

Selon l’expression de $K_{A}$:

$K_{A}=\frac{\left(\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]_{\hat{e} q}\right)^{2}}{C_{A}-\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]_{\hat{\varepsilon} q}}$

On a :

$\tau=\frac{\left[\mathrm{H}_{3} \boldsymbol{O}^{+}\right]_{\text {éq }}}{C_{A}} \rightarrow\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]_{\mathrm{e} q}=\tau \cdot \mathrm{C}_{\boldsymbol{A}}$ $K_{A}=\frac{\left(\tau \cdot C_{A}\right)^{2}}{C_{A}-\tau \cdot C_{A}}=\frac{C_{A} \cdot \tau^{2}}{1-\tau}$

La valeur de la constante $K_{A}$ augmente avec l’augmentation de la valeur de .

$\begin{gathered} \tau\left(\mathrm{HCOOH} \mathrm{HCOO}^{-}\right)>\tau\left(\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{COOH} \mathrm{C}_{2} \mathrm{H}_{5} \mathrm{COO}^{-}\right) \\ \rightarrow \mathrm{K}_{A}\left(\mathrm{HCOOHHCOO}^{-}\right)  >\mathrm{K}_{A}\left(\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{COOH} \mathrm{C}_{2} \mathrm{H}_{5} \mathrm{COO}^{-}\right) \end{gathered}$

→ La constante d’acidité de l’acide méthanoïque est plus grande que celle de l’acide propanoïque.