1.1 L’équation de la réaction de dosage est:

$N H_{3(a q)}+H_{3} O_{(a q)}^{+} \longrightarrow N H_{4(a q)}^{+}+H_{2} O$

1.2 à l’équivalence, nous avons:

$\begin{aligned}n_{b}\left(NH_{3}\right) &=n_{a}\left(H_{3} 0^{+}\right) \\ C_{b} \cdot V_{b} &=C_{a} \cdot V_{a E} \end{aligned}$

1.3 On a:

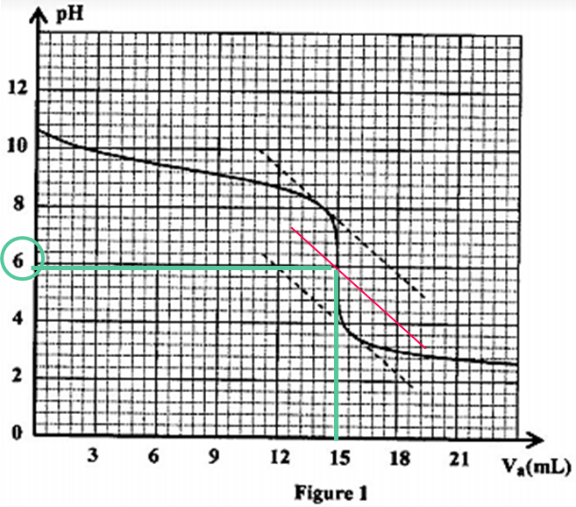
$\begin{array}{c} C_{b} . V_{b}=C_{a} . V_{a E} \\ C_{b}=C_{a} \cdot \frac{V_{a E}}{V_{b}} \\ C_{b}=10^{-2} \times \frac{15}{15}=10^{-2} \text { mol. } L^{-1} \end{array}$

On a dilué la solution $S_{0}$ 100 fois pour obtenir la solution $S_{b}$

$C_{0}=100 C_{b}=1 \text { mol. } L^{-1}$

1.4

2.1 L’équation de la réaction entre l’ammoniac et l’eau :

$N H_{3(a q)}+H_{2} O \quad \rightleftharpoons \quad N H_{4(a q)}^{+}+H O_{(a q)}^{-}$

2.2 On a :

$\begin{array}{c} {\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]_{\mathrm{e} \mathrm{q}} \cdot\left[\mathrm{HO}^{-}\right]_{\dot{e} q}=K_{e}} \\ {\left[\mathrm{HO}^{-}\right]_{\mathrm{e} q}=\frac{K_{e}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]_{\mathrm{e} q}}=\frac{10^{-14}}{10^{-p H}}=10^{p H-14}} \\ {\left[\mathrm{HO}^{-}\right]_{\mathrm{e} q}=3,98.10^{-4} \mathrm{mol.} L^{-1}} \end{array}$

2.3 Le taux d’avancement final de cette réaction est:

$\tau=\frac xe qx\max$

D’après le tableau d’avancement : $n_{e q}\left(H 0^{-}\right)=x_{e q}=\left[H O^{-}\right]_{e q} . V$

On suppose que la réaction est totale et puisque l’eau est en excès, alors le réactif limitant est l’ammoniac NH3 c.à.d:

$\begin{array}{c} C_{b} \cdot V-x_{\max }=0 \\ x_{\max }=C_{b} \cdot V \\ \tau=\frac{\left[H O^{-}\right]_{\varepsilon q}}{V}=\frac{3,98.10^{-4}}{10^{-2}}=3,98 \% \end{array}$

2.4 Le quotient de la réaction à l’équilibre est:

$Q_{r, \text { éq }}=\frac{\left[N H_{4}^{+}\right]_{e q} \cdot\left[H O^{-}\right]_{e q}}{\left[N H_{3}\right]_{e q}}$

D'après le tableau d'avancement:

$\begin{array}{c} n_{e q}\left(N H_{4}^{+}\right)=n_{e q}\left(H O^{-}\right)=x_{e q} \\ {\left[N H_{4}^{+}\right]_{e q}=\left[H O^{-}\right]_{e q}=\frac{\mathrm{x}_{e q}}{V}} \\ {\left[N H_{3}\right]_{e q}=\frac{C_{b} \cdot V-x_{e q}}{V}=C_{b}-\frac{x_{e q}}{V}=C_{b}-\left[H O^{-}\right]_{e q}} \\ Q_{r, i q}=\frac{\left[H O^{-}\right]^{2}{ }_{e q}}{C_{b}-\left[H O^{-}\right]_{e q}} \\ Q_{r, \dot{e} q}=\frac{\left(3,98 \cdot 10^{-4}\right)^{2}}{10^{-2}-3,98 \cdot 10^{-4}} \end{array}$

$Q_{r, é q}=1,65.10^{-5}$

2.5 La valeur du $p K_{A}$ du couple $N H_{4}^{+} / N H_{3}:$

On a:

$Q_{r, \dot{\text { eq }}}=\frac{\left[\mathrm{NH}_{4}^{+}\right]_{\text {eq }}\left[\mathrm{HO}^{-}\right]_{\text {eq }}}{\left[\boldsymbol{N H}_{3}\right]_{\text {eq }}}$

On multiplie le numérateur et le dénominateur par $\left[H_{3}O^{+}\right]_{\text {éq }}$ :

$Q_{r, \text { éq }}=\frac{\left[N H_{4}^{+}\right]_{\text {éq }} \cdot\left[\text { HO }^{-}\right]_{\text {éq }}}{\left[N H_{3}\right]_{éq}} \times \frac{\left[H_{3} O^{+}\right]_{\text {éq }}}{\left[H_{3} O^{+}\right]_{\text {éq }}}$

Donc:

$\begin{array}{l} Q_{r, éq}=\frac{K_{e}}{K_{A}} \\ K_{A}=\frac{K_{e}}{Q_{r, éq}} \end{array}$

Donc:

$\begin{array}{c} p K_{A}=-\log K_{A}=-\log \frac{K_{e}}{Q_{r, éq}} \\ p K_{A}=-\log \frac{10^{-14}}{1,65 \cdot 10^{-5}} \\ p K_{A}=9,2 \end{array}$

Partie 2:

1. Après une durée $\Delta t$ de fonctionnement de la pile, on observe un dépôt sur l’électrode d’argent et une diminution de la masse de l’électrode de chrome.

$C r_{(s)} \longrightarrow C r_{(a q)}^{3+}+3 e^{-}$

L’électrode d’une Chrome est une anode.

L’anode c’est l’électrode à côté de la quelle, il y a oxydation (perte d’électrons) donc la masse de cette électrode diminue, dans ce cas c’est l’électrode de Chrome.

2. Le schéma conventionnel de la pile:

3. Les équations aux électrodes et l’équation bilan:

• Au niveau de l’anode: oxydation anodique

$C r_{(s)} \quad \longrightarrow \quad C r_{(a q)}^{3+}+3 e^{-}$

• Au niveau de la cathode: réduction cathodique

• Equation bilan du fonctionnement de la pile:

$C r_{(s)}+3 \mathrm{Ag}_{(a q)}^{+} \longrightarrow C r_{(a q)}^{3+}+3 A g_{(s)}$

4. On a : la quantité de matière d’électron échangé est $n\left(e^{-}\right)=\frac{Q}{F}$

D’après le tableau d’avancement:

$n(\boldsymbol{C r})=x=\frac{m(C r)}{M(\mathrm{Cr})}$ quantité de matière du chrome qui réagit.

On sait que le nombre d’électron échangé est 3,

alors $\boldsymbol{n}\left(\boldsymbol{e}^{-}\right)=3 \mathrm{x} \rightarrow x=\frac{n\left(e^{-}\right)}{3}=\frac{m(\boldsymbol{C r})}{M(\mathrm{Cr})}$

La variation de la masse du chrome est:

$\begin{array}{c} \Delta m=m_{f}(C r)-m_{i}(C r)=\left(m_{i}(C r)-m(C r)\right)-m_{i}(C r)=-m(C r) \\ \Delta m=-\frac{Q}{3 \cdot F} \cdot M(C r) \\ \Delta m=-\frac{5,79}{3 \times 96500} \times 52=-1,04.10^{-3} g \end{array}$