1. Donner le nom de l’électrode (anode ou cathode) au niveau de laquelle se forme le dibrome. C’est l’anode (qui attire l’anion $$\mathrm{B} r^{-}$$)
2. Ecrire les équations des réactions aux électrodes, ainsi que l’équation bilan lors de l’électrolyse.
- Au niveau de la cathode : $$P b_{(a q)}^{2+}+2 e^{-} \rightleftarrows P b_{(s)}$$
- Au niveau de l’anode : $$\text { 2. } B r_{(a q)}^{-} \rightleftarrows B r_{2(g)}+2 e^{-}$$
- Equation bilan : $$P b_{(a q)}^{2+}+2 . B r_{(a q)}^{-} \rightleftarrows P b_{(s)}+B r_{2(g)}$$
3. Déterminer la valeur de l’intensité I du courant électrique passant dans le circuit pendant la durée $$\Delta t$$.
On sait que $$I=\frac{\text { Quantité d’électricité }}{\text { Durée du temps }}=\frac{Q}{\Delta t}$$
Avec $$Q=n\left(e^{-}\right) \times F$$
Et d’après le tableau d’avancement, $$n\left(e^{-}\right)=2 x \text { et } x=n_{t}(P b)=\frac{m}{M(P b)}$$
Combinant ces relations, on aboutit à l’expression :
$$I=\frac{\text { 2. } m \cdot F}{M(P b) \cdot \Delta t}=\frac{2 \times 20,72 \times 9,56.10^{4}}{207,2 \times 3600}=5,36 A$$
4. Calculer, dans les conditions de l’expérience, le volume V du gaz dibrome formé pendant $$\Delta t$$.
Le tableau d’avancement :
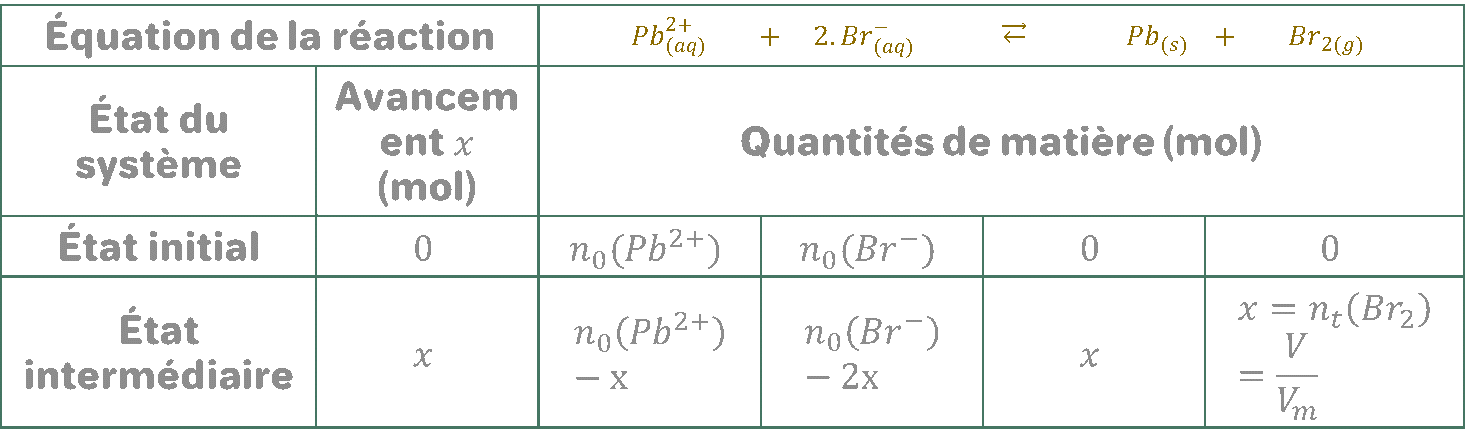
D’après les deux tableaux : $$x=\frac{m}{M(P b)} \text { et } x=n_{t}\left(B r_{2}\right)=\frac{V}{V_{m}}$$
On déduit que : $$V=\frac{m \cdot V_{m}}{M(P b)}=\frac{20,72 \times 70,5}{207,2}=7,05 L$$