CHIMIE

Partie I

1- Solution aqueuse d'hydroxyde de sodium:

- Expression du $\mathrm{pH}$ :

On a : $~~\mathrm{Ke}=\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \times\left[\mathrm{HO}^{-}\right]$

Soit : $~~\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\frac{\mathrm{Ke}}{\left[\mathrm{HO}^{-}\right]}=\frac{\mathrm{Ke}}{\mathrm{C}_{\mathrm{B}}}$

Et: $~~\mathrm{pH}=-\log \left[\mathrm{H}_3 \mathrm{O}^{+}\right]=-\log \frac{\mathrm{Ke}}{\mathrm{C}_{\mathrm{B}}}$

Donc: $\quad \mathrm{pH}=-\log \mathrm{Ke}+\log \mathrm{C}_{\mathrm{B}}\\[0.5cm]$

1.2 - Valeur de $C_B$.

On a : $~~\mathrm{pH}=-\log \frac{\mathrm{Ke}}{\mathrm{C}_{\mathrm{B}}}$

Donc : $~~10^{-\mathrm{pH}}=\frac{\mathrm{Ke}}{\mathrm{C}_{\mathrm{B}}}$

Soit : $~~\mathrm{C}_{\mathrm{B}}=\frac{\mathrm{Ke}}{10^{-\mathrm{pH}}} =\mathrm{Ke} \times 10^{\mathrm{pH}}$

Application numérique :

$$C_B=10^{-14} \times 10^{12,7}=5 \times 10^{-2} \mathrm{~mol} . \mathrm{L}^{-1}\\[0.5cm]$$

2. Contrôle de la qualité d'un lait de vache :

2.1- Équation de réaction de dosage :

$\mathrm{HA}_{\text {(aq) }}+\mathrm{HO}_{(\text {aq })}^{-} \longrightarrow \mathrm{A}^-_{(\text {aq })}+\mathrm{H}_2 \mathrm{O}_{(\ell)}\\[0.5cm]$

2.2- Expression de $\mathrm{C}_{\mathrm{A}}$ :

* Tableau d'avancement :

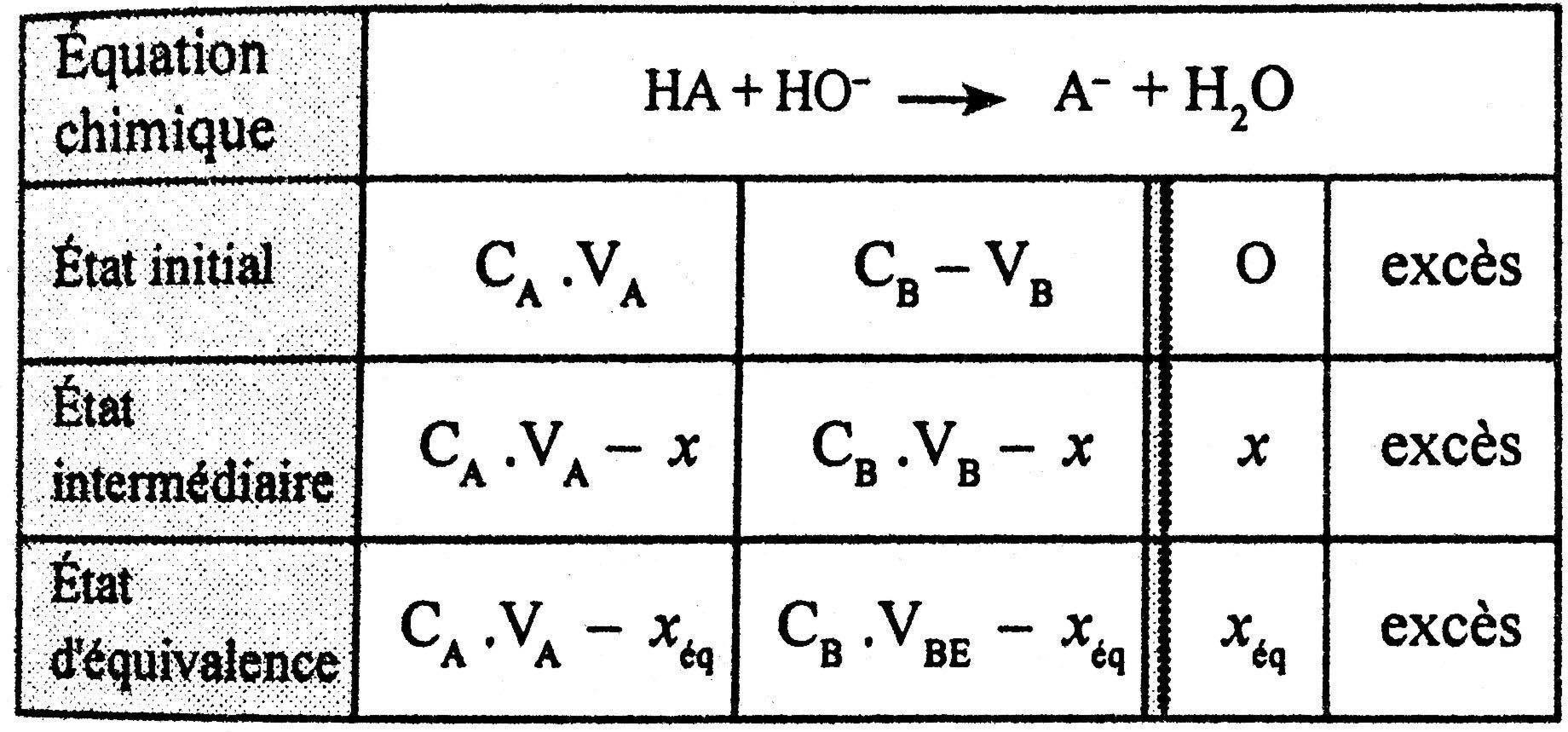
A l'équivalence ; les deux réactifs sont totalement consommés ;

donc: $~~\mathrm{C}_{\mathrm{A}} \cdot \mathrm{V}_{\mathrm{A}}-x_{\text{éq}}=0$

soit : $~~x_{\text{éq}}=\mathrm{C}_{\mathrm{A}} \cdot \mathrm{V}_{\mathrm{A}}$

$\mathrm{C_B \cdot V_{B E}}-x_{\text{éq}}=0~~$ soit : $~~x_{\text{éq}}=\mathrm{C_B \cdot V_{B E}}$

Donc : $~~\mathrm{C}_{\mathrm{A}} \cdot \mathrm{V}_{\mathrm{A}}=\mathrm{C}_{\mathrm{B}} \cdot \mathrm{V}_{\mathrm{BE}}$

Soit : $~~\mathrm{C}_{\mathrm{A}}=\frac{\mathrm{C}_{\mathrm{B}} \cdot \mathrm{V}_{\mathrm{BE}}}{\mathrm{V}_{\mathrm{A}}}\\[0.5cm]$

2.2- On a la relation:

$\mathrm{K}_{\mathrm{A}}=\frac{\left[\mathrm{A}^{-}\right] \times\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{[\mathrm{AH}]}~~$ soit : $~\left[\mathrm{A}^{-}\right] \times\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\mathrm{K}_{\mathrm{A}} \cdot[\mathrm{AH}] $

D'après le tableau d'avancement précèdent :

On a : $~~\left[\mathrm{A}^{-}\right]=\frac{x}{\mathrm{~V}_{\mathrm{A}}+\mathrm{V}_{\mathrm{B}}}~~$ et $~~[\mathrm{AH}]=\frac{\mathrm{C}_{\mathrm{A}} \cdot \mathrm{V}_{\mathrm{A}}-x}{\mathrm{~V}_{\mathrm{A}}+\mathrm{V}_{\mathrm{B}}}$

D'où : $~~\frac{x}{\mathrm{~V}_{\mathrm{A}}+\mathrm{V}_{\mathrm{B}}} \times 10^{\mathrm{pH}}=\mathrm{K}_{\mathrm{A}} \cdot\left(\frac{\mathrm{C}_{\mathrm{A}} \cdot \mathrm{V}_{\mathrm{A}}-x}{\mathrm{~V}_{\mathrm{A}}+\mathrm{V}_{\mathrm{B}}}\right)$

Donc $: ~~x \times 10^{\mathrm{pH}}= \mathrm{K}_{\mathrm{A}} \left(\mathrm{C}_{\mathrm{A}} \cdot \mathrm{V}_{\mathrm{A}}-x\right)$

Avec $: ~~\mathrm{C_A \cdot V_A=C_B \cdot V_{B E}}$

Et pour : $~0<\mathrm{V}_B<\mathrm{V}_{\mathrm{BE}}~$ on est avant l'équivalence donc $\mathrm{HO}^{-}$ est le réactif limitant: $~\mathrm{C}_B \cdot \mathrm{V}_B-x=0~$ soit : $~x=\mathrm{C}_B \cdot \mathrm{V}_B$

Ainsi : $~~ \mathrm{C_B \times V_B} \times 10^{-\mathrm{pH}}=\mathrm{K_A \cdot\left(C_A \cdot V_{B E}-C_B \cdot V_B\right)}$

Soit: $~~\mathrm{C_B \times V_B \times 10^{-p H}=K_A \cdot\left(V_{B E}-V_B\right) \cdot C_B}$

Donc: $\quad \mathrm{V_B \cdot 10^{-p H}=K_A \cdot\left(V_{B E}-V_B\right)}\\[0.5cm]$

2.4- Étude graphique :

2.4.1- * Volume $\mathrm{V}_{\mathrm{BE}}$ :

D'après le tableau d'avancement précèdent $~\left(\mathrm{V}_{\mathrm{B}}\cdot 10^{-\mathrm{pH}}\right)~$ s'annule pour $~\mathrm{V}_{\mathrm{B}}=\mathrm{V}_{\mathrm{BE}}$

Et graphiquement $~\left(10^{-\mathrm{PH}} \times \mathrm{V}_{\mathrm{B}}\right)~$ s'annule lorsque la courbe coupe l'axe des abscisses .

C'est -à-dire pour : $~~\mathrm{V}_{\mathrm{BE}}=\mathrm{V}_{\mathrm{B}}=12,4 \mathrm{~mL}$.

* Concentration $\mathrm{C}_{\mathrm{A}}$ :

On a: $~~\mathrm{C}_{\mathrm{A}}=\frac{\mathrm{C}_{\mathrm{B}} \times \mathrm{V}_{\mathrm{BE}}}{\mathrm{V}_{\mathrm{A}}}=\frac{5 \times 10^{-2} \times 12,4}{25}$

Soit : $ ~~\mathrm{C_A=2,48 \times 10^{-2}} \mathrm{mo \ell} \cdot \mathrm{L}^{-1}\\[0.5cm]$

2.4.2- Valeur de $\mathrm{pK}_{\mathrm{A}}$ :

D'après l'équation de la droite affine ; la valeur $\left(\mathrm{K}_{\mathrm{A}} \times \mathrm{V}_{\mathrm{B}}\right)$ est le point d'intersection de la droite avec l'axe des ordonnées :

Soit : $~~\mathrm{K}_{\mathrm{A}} \times \mathrm{V}_{\mathrm{BE}}=15,5 \times 10^{-4} \mathrm{~mL}$

D'où : $~~\mathrm{K}_{\mathrm{A}}=\frac{15,5 \times 10^{-4}}{\mathrm{~V}_{\mathrm{BE}}}=\frac{15,5 \times 10^{-4}}{12,4}$

Donc $:~~ \mathrm{K}_{\mathrm{A}}=1,25 \times 10^{-4}$

Et $:~~ \mathrm{pK}_{\mathrm{A}}=-\log \mathrm{K}_{\mathrm{A}}=-\log \left(1,25 \times 10^{-4}\right)$

$\mathrm{pK}_{\mathrm{A}}=3,9\\[0.5cm]$

2.5-Qualité du lait étudié :

* Calcul de la masse de l'acide lactique dans le volume $V=1 \mathrm{~L}$ de lait.

On a: $~~\mathrm{n=C_A \times V_A=\frac{m}{M}}$

Soit : $~~\mathrm{m=C_A \times V \times M}$

Donc $:~~ \mathrm{m}=2,48 \times 10^{-2} \times 1 \times 90=2,232 \mathrm{~g}$

* Acidité de ce lait :

$1^{\circ} \mathrm{D}$ correspond à la masse $1 \times 10^{-1} \mathrm{~g}$ d'acide .

Ainsi la masse $\mathrm{m}=2,232 \mathrm{~g}$ d'acide correspond à : $22,32^{\circ} \mathrm{D}$

Donc ce lait n'est pas frais.$\\[0.5cm]$

Partie II : Pile chrome - argent

1-Équation de réaction :

Au pôle négatif : $~~\mathrm{Cr}_{(\mathrm{s})} \rightleftharpoons \mathrm{Cr}_{(\mathrm{aq})}^{3^{+}}+3 \mathrm{e}^{-}$

Au pôle positif : $~~\mathrm{Ag}_{(\mathrm{aq})^{+}}^{+}+\mathrm{e}^{-} \rightleftharpoons \mathrm{Ag}_{(\mathrm{s})}$

L'équation bilan de fonctionnement de la pile :

$\mathrm{Cr}_{(\mathrm{s})}+3 \mathrm{Ag}_{(\mathrm{aq})}^{+} \longrightarrow \mathrm{Cr}_{(\mathrm{aq})}^{3^{+}}+3 \mathrm{Ag}_{(\mathrm{s})}\\[0.5cm]$

2-Avancement de la réaction:

A l'instant $\mathrm{t}_1$; la quantité de matière du chrome consommée est : $~~\mathrm{n}(\mathrm{Cr})=\left|\mathrm{n}_1(\mathrm{Cr})-\mathrm{n}_{\mathrm{i}}(\mathrm{Cr})\right|=\mathrm{t}_1$

D'où : $~~x_1=\frac{\mathrm{m}(\mathrm{Cr})}{\mathrm{M}(\mathrm{Cr})}=\frac{52 \times 10^{-3}}{52}=10^{-3} \mathrm{mo} \ell.\\[0.5cm]$

3 - Concentration des ions $\mathrm{Cr}^{3+}$ à l'instant $\mathrm{t}_{1}$:

$\left[\mathrm{Cr}^{3+}\right]=\frac{\mathrm{C}_1 \times \mathrm{V}+x_1}{\mathrm{~V}}=\mathrm{C}_1+\frac{x_1}{\mathrm{~V}}$

$\left[\mathrm{Cr}^{3+}\right]=0,1+\frac{10^{-3}}{0,1}=0,11 \mathrm{~mol} \cdot \mathrm{L}^{-1}\\[0.5cm]$

4- La valeur de l'instant $t_1$ :

On a la relation: $~~I_0 \times \Delta t=n\left(e^{-}\right) \times F$

Soit : $~~\Delta \mathrm{t}=\frac{n\left(e^{-}\right) \times F}{I_0}=\frac{3 \cdot x \cdot F}{I_0}$

$$\Delta \mathrm{t}=\frac{3 \times 10^{-3} \times 9,65 \times 10^4}{50 \times 10^{-3}}=5790 \mathrm{~S} .$$

Avec $~\mathrm{t}_0=0~$ et $~\Delta \mathrm{t}=\mathrm{t}_1-\mathrm{t}_0=\mathrm{t}_1=5790 \mathrm{~S}$.