CHIMIE
I- Suivi temporel d'une transformation chimique :
1- Expression l'avancement de la réaction:
* Tableau d'avancement :

* L'équation d'état des gaz parfaits s'écrit pour le gaz CO2 produit, à l'instant t:
P⋅V(CO2)=n(CO2)⋅RT soit n(CO2)=R⋅TP⋅V(CO2)
D'après le tableau d'avancement on a:
n(CO2)=x
D'où : x=R⋅TP⋅V(CO2)
Soit : x=8,31×2981,02×105⋅V(CO2)=41,189⋅V(CO2)
Ainsi : x=41,2⋅V(CO2)
2- Temps de demi-réaction t1/2 :
t1/2 est l'abscisse du point de la courbe qui correspond au volume V(CO2)=2V(CO2)max
Graphiquement V(CO2)max=60 mL
et t1/2: V(CO2)=30 mℓ
Par projection sur la courbe ; puis sur l'axe des abscisses on obtient : t1/2≈120 s.
3- La vitesse volumique de réaction :
On sait que : V= Vs1×dtdx
Avec : x=41,2×V(CO2)
Donc : dtdx=41,2⋅dtdV(CO2)
D'où : v= Vs1×41,2×dtdV(CO2)
A l'instant t1: v(t1)=0,1×10−31×41,2×(560−0)(60−33,6)×10−6
Soit : v(t1)=1,94×10−2 mol⋅m−3⋅s−1.
II- Dosage acido-basique :
1- Équation chimique du dosage :
NH3(aq)+H3O(aq)+⟶NH4(aq)++H2O(ℓ)
2- Graphiquement ; le volume du titrant ajouté à l'équivalence est : VAE=10 mL.
3- * A l'équivalence du dosage ; On a: CA×VAE=CB×VB
D'où : CB=VBCA×VAE=202×10−2×10
CB=10−2 mol⋅L−1
Concentration molaire du détergent : On a : CB=100CD (dilution 100 fois)
Soit : CD=100×CB=100×10−2
CD=1 mol⋅L−1
4- Solution aqueuse de l'ammoniac :
4.1- Équation chimique :
NH3(aq)+H2O(ℓ)⇌NH4 (aq) ++HO(aq)−
4.2- Le pH de la solution avant le dosage correspond à sa valeur pour: VA=0
soit graphiquement : pH=10,6.
4.3- Concentration effective des ions :
* Tableau d'avancement :

[NH4+]= VBxf=[HO−]=[H3O+]Ke
D'où : [NH4+]=10−10,610−14≈4×10−4 mol⋅L−1.
[NH3]= VBCB⋅VB−xf=CB− VBxf
=CB−[NH4+]=10−2−4×10−4=9,6×10−3 mol−1 L−1
4.4- Calcul du pKA du couple étudié :
On a la relation: pH=pKA+log[NH4+][NH3]
Soit : pKA=pH−log[NH4+][NH3]
Donc: pKA=10,6−log(209,6×10−3)=9,22
5- Valeur de pKA à partir des trois graphes :
On a : pKA=pH−log([NH4+][NH3])
* D'après la figure (3); pour VA=5 mL
On a : [NH3]=[NH4+]
D'où la relation devient : pKA=pH
* A partir de la figure (2) ; pour VA=5 mL
On a : pH=9,2
Ainsi on retrouve : pKA=9,2.
6-6.1-La solution ( Si) est une solution d'ammoniac, donc NH3(aq) y est majoritaire.
Au fur et à mesure de l'ajout de la solution (SA); la concentration de NH3(aq) décroit progressivement.
Donc la courbe (3) qui correspond à l'évolution de [NH3] en fonction de VA
6.2- * A partir de la courbe (1) ; on a pour : pH=8,8 le volume VA=7,2 mL.
* On utilise la courbe (3) ; on obtient par projection : [NH3]=2×10−3 mol
III- Électrolysé d'une solution aqueuse d'acide chlorhydrique :
1- Au niveau de l'anode ; il se produit une réaction d'oxydation d'équation :
2ℓ(aq)−⇌Cℓ2( g)+2e−
2- Au niveau de la cathode ; il se produit une réduction d'équation:
2H3O(aq)++2e−⇌H2( g)+2H2O
L'équation bilan de cette électrolyse est donc :
2Cl(aq)−+2H3O(aq) +→Cl2( g)+H2( g)+2H2O
3- * Il faut calculer la concentration des ions H3O+:
pH=−log[H3O+]
* On a les deux relations : Q=I×Δt=n(e−)×F
Soit : I×Δt=2⋅x×F
D’ouˋ : xx=2×FI×Δt=2×9,65×1040,5×30×60=4,66×10−3moℓ
* Tableau d'avancement réduit :
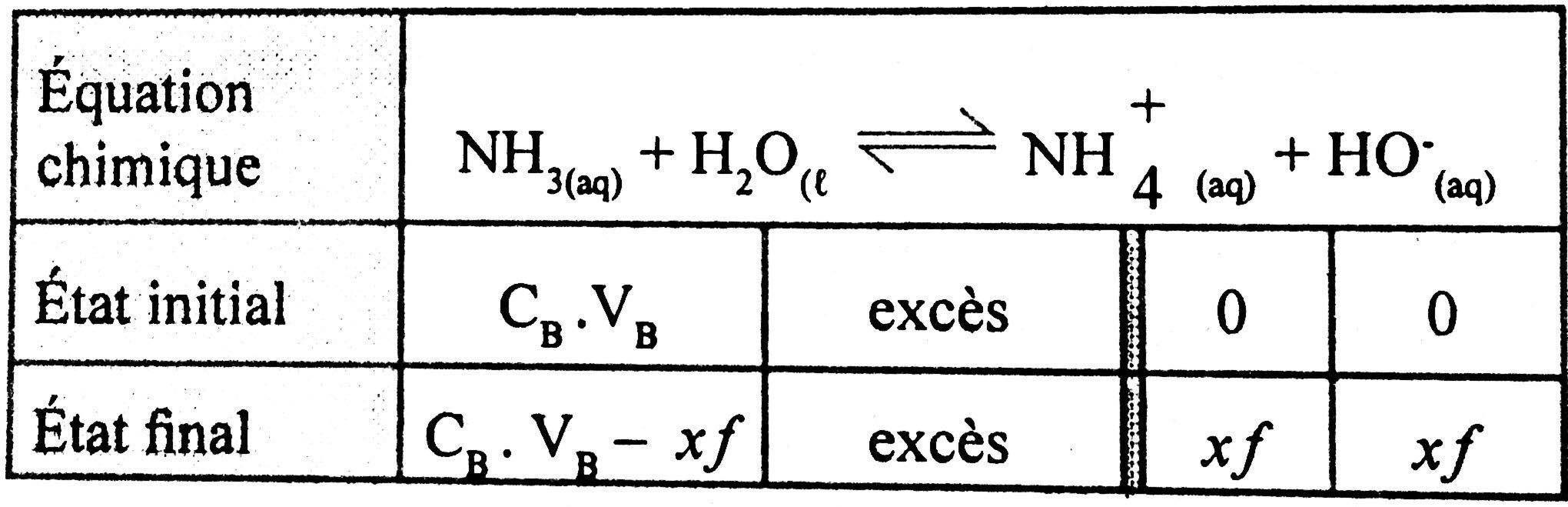
Ainsi : [H3O+]= V0C0 V0−2x=C0−2 V0x
[H3O+]=5×10−2−2×0,54,66×10−3=3,136×10−2 mol.L−1
Donc : pH=−log(3,136×10−2)=1,5.