Partie I :
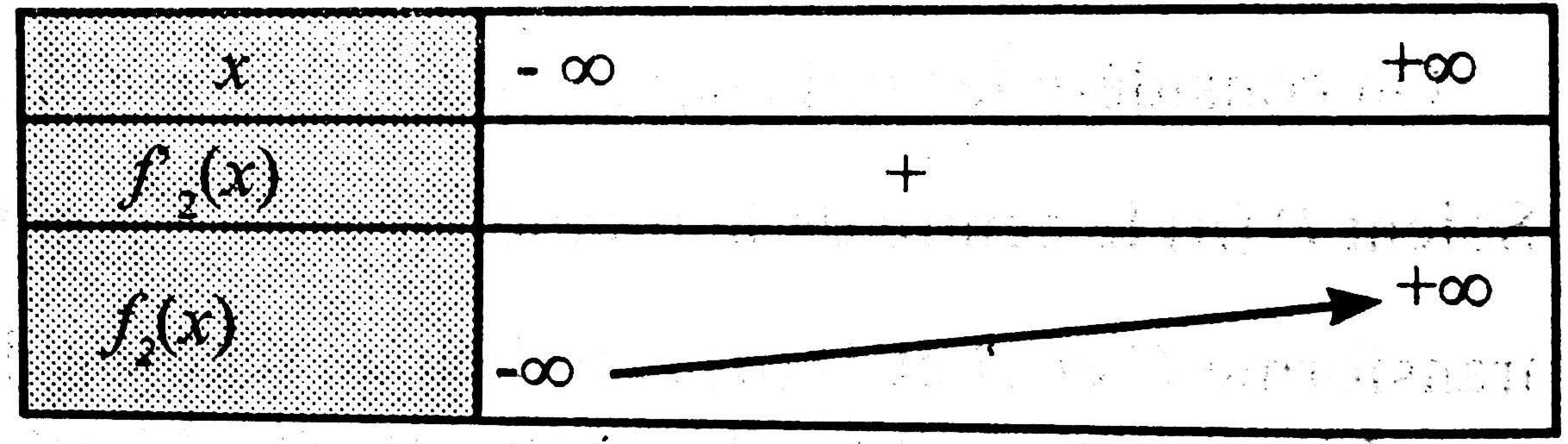
1-a. x→+∞lim(fn(x)−xn+2)=x→+∞lim1+ex−2ex+2=x→+∞lim1+ex−2ex=0. ( car x→+∞limex=+∞)
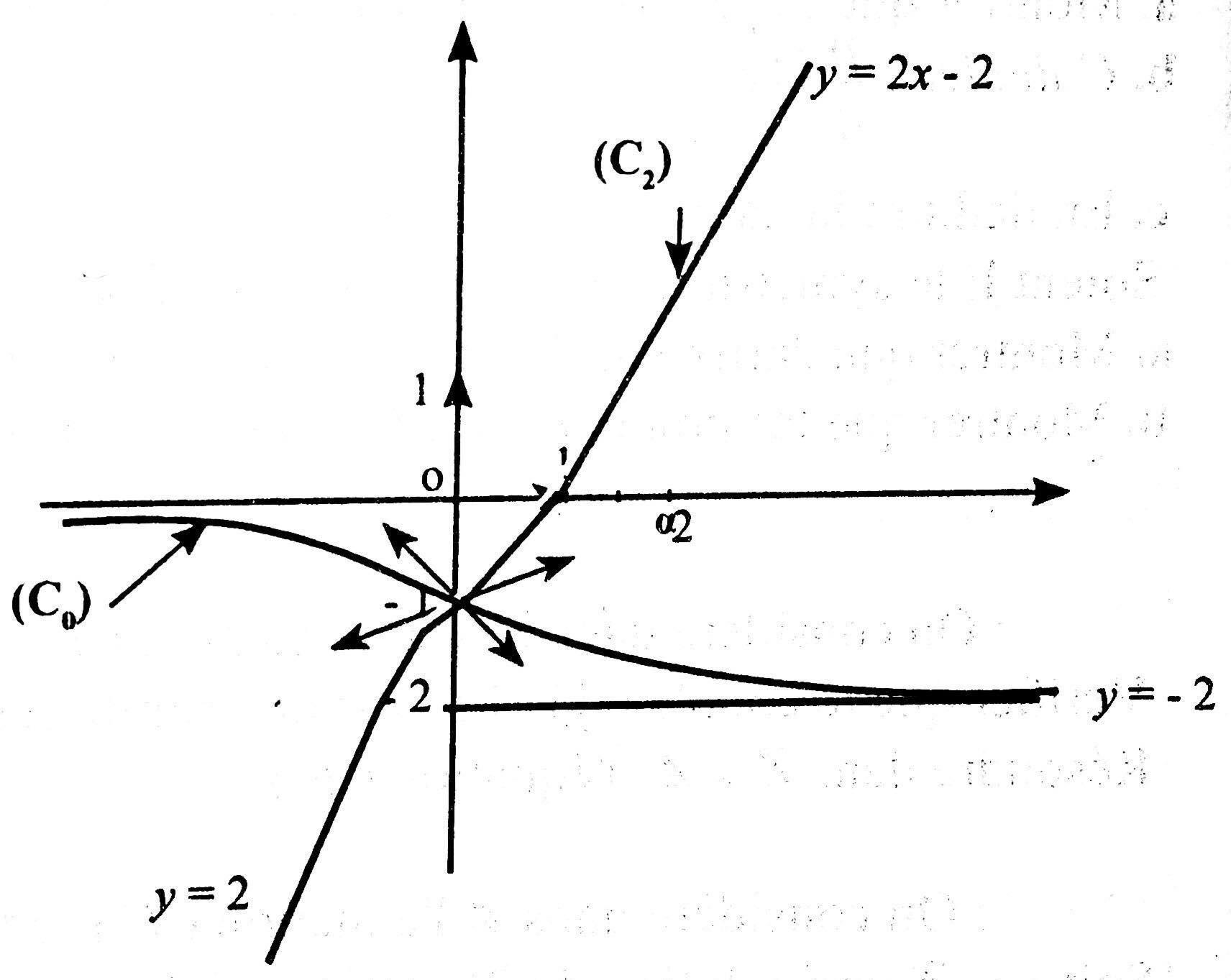
Donc (Cn) admet une asymptote oblique au voisinage de +∞; d'équation y=xn−2.
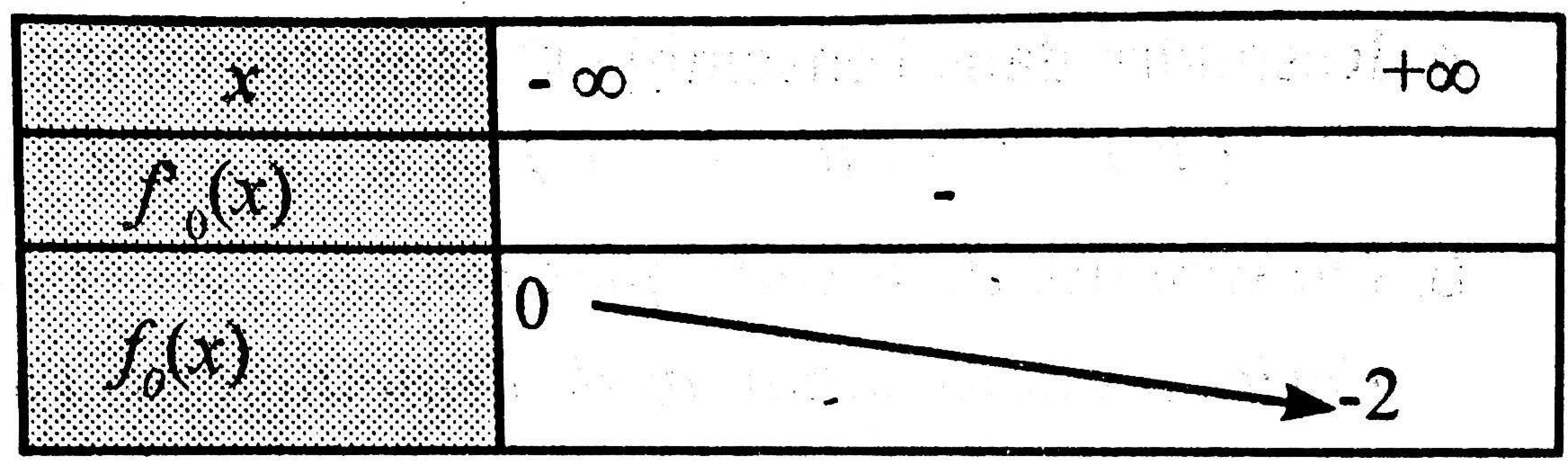
b. On a x→+∞limfn(x)=−∞ et x→+∞limfn(x)−xn=0
(car x→+∞limex=0)
Donc (Cn) admet une asymptote oblique (Δ) au voisinage de −∞ ; d'équation y=xn.
2- a. fn est dérivable sur R comme somme et quotient des fonctions dérivables sur R.
(∀x∈R) ; fn′(x)=−2(1+ex−2ex)+n=−2((1+ex)2ex(1+ex)−e2x)+n=(1+ex)2−2ex+n
b. On a: (∀x∈R) ; (1+ex)24ex−1=(1+ex)24ex−(1+ex)2
(1+ex)24ex−1=(1+ex)2−e2x+2ex−1=(1+ex)2−(e2x−1)2≤0
D'où (∀x∈R) ; (1+ex)24ex≤1
Puisque (1+ex)24ex≤1;
alors (1+ex)22ex≤21
D'où n−(1+ex)22ex≥n−21
Si n≥1 ; alors n−21>0 ; d'où fn′(x)>0. Pour tout x de R
Par suite fn strictement croissante sur R
3- a. L'équation de la tangente à (Cn) au point I est :
y=fn′(0)x+fn(0)
D'où y=(n−21)x−1
b. On a : (∀x∈R) ; fn′(x)=(1+ex)2−2ex+n
Donc (∀x∈R) ; fn′′(x)=−2((1+ex)4ex(1+ex)2−2e2x(1+ex))
=(1+ex)4−2ex(1+ex)(1+ex−2ex)
=(1+ex)32ex(ex−1)
Le signe de fn′′(x) est celui de ex−1; car
(∀x∈R) ; (1+ex)32ex>0
ex−1 s'annule en 0 et change de signe à gauche et à droite de 0 ; donc de même pour fn′′(x);
par suite le point I est le seul point d'infléxion de la courbe (Cn).
4-Tracé de (C0) et (C2)
On a :
et
1- a. On a: (∀t>0)
A(t)=∫0t∣fn(x)−(nx−2)∣dx( cm2)=∫0t∣∣1+ex2∣∣dx( cm2)=∫0t1+ex2dx( cm2)=2∫0t(1−1+exex)dx( cm2)=2[x−ln(1+ex)]0t( cm2)=2[t−ln(1+et)+ln2](cm2)
b. t→+∞limA(t)=t→+∞lim2[t−ln(1+et)+ln2]=t→+∞lim2[t−lnet−ln(1+e−t)+ln2]=t→+∞lim2[ln2−ln(1+e−t)]=2ln2(Cm2)
Partie II
u0=0 et (∀n∈N) ; un+1=f0(u0)
1- a. On pose pour tout x de R; g(x)=f0(x)−x
g est une fonction continue sur R, et dérivable sur R et (∀x∈R) ; g′(x)=f0′(x)−1<0.
D'où g est strictement décroissante sur R. et on a :
g(R)=R et 0∈R;
donc l'équation g(x)=0 (c aˋ d : f0(x)=x) admet une solution unique α dans R.
b. On a : (∀x∈R) ; f0′(x)=(1+ex)2−2ex
D'où ∣f0′(x)∣=(1+ex)22ex≤21( d'aprés I/2) a)
2- a.On a f0 est continue sur le segment d'extrémités Un et α; et dérivable sur l'intervalle d'extrémités Un et α;
donc d'aprés T.A.F.
∃c∈]Un;α[; f0(Un)−f0(α)=f0(c)(Un−α)
D' où ∣f0(Un)−f0(α)∣=∣f0′(c)∣∣Un−α∣
Par suite : (∀x∈R) ; ∣Un+1−α∣≤21∣Un−α∣
b. Par recurrence :
Pour n=0 ; on a : ∣U0−α∣=∣α∣ et (21)0∣α∣=∣α∣
Donc ∣U0−α∣≤(21)0∣α∣
Soit n∈N ; supposons que ∣Un−α∣≤(21)n∣α∣
et montrons que ∣Un+1−α∣≤(21)n+1∣α∣.
On a: ∣Un+1−α∣≤21∣Un−α∣.
et 21∣Un−α∣≤(21)n+1∣α∣
Donc ∣Un+1−α∣≤(21)n+1∣α∣
Par suite (∀n∈N); ∣Un−α∣≤(21)n∣α∣
c. On a : (∀n∈N) ; ∣Un−α∣≤(21)n∣α∣
et puisque n→+∞lim(21)n∣α∣=0(car −1<21<1)
alors n→+∞lim∣Un−α∣=0;
par suite n→+∞limUn=α
Partie III
1- a. Pour tout n≥2; fn est une fonction continue est strictement croissante sur R; f(R)=R et 0∈R;
donc l'équation fn(x)=0 admet une solution unique xn dans R.
b.On a : fn(0)=−1 et fn(1)=1+e−2e+n=1+e(n−2)e+n>0
Donc (∀n≥2) ; 0<xn<1.
2.a. On a: (∀n≥2) ; fn+1(x)−fn(x)=x
Donc fn+1(xn)−fn(xn)=xn
et puisque ∀n≥2; xn>0 et fn(xn)=0
alors: fn+1(xn)>0
b. On a : (∀n≥2);fn+1(xn)>0 et on sait que fn+1(xn+1)=0
alors (∀n≥2) ; fn+1(xn)>fn+1(xn+1)
Or on sait que : ∀n≥2) ; fn+1 est continue et strictement croissante
Donc fn+1 est bijective par suite (∀n≥2) ;xn>xn+1
Donc la suite (xn)n est strictement décroissante.
b. la suite (xn)n est décroissante et minorée par 0 ; donc elle est convergente.
3- a. On a d'une part :
(∀n≥2) ; fn(n1)=1+e1/n−2e1/n+1=1+e1/n1−e1/n<0
et on sait que fn(1)>0; donc
(∀n≥2);n1⟨xn<1∗ D’autre part on a : (∀n≥2) ; fn(x)=0fn(xn)=0⇔nxn=1+exn2exn=2−1+exn2n
On sait que : (∀n≥2) ;xn<1
Donc 1+exn<1+e D'où 1+exn−2<1+e−2
Donc 2−1+exn2<2−1+e2
Par suite (∀n≥2) ; nxn<2−1+e2=1+e2e
D'où (∀n≥2) ; xn<n1(1+e2e).
Conclusion :
(∀n≥2);n1<xn<n1(1+e2e)
b. On a : (∀n≥2) ; n1<xn<n1(1+e2e).
et puisque : n→+∞limn1=0 et n→+∞limn1(1+e2e)=0
alors n→+∞limxn=0
Puisque : (∀n≥2) ; nxn=1+exn2exn
Donc limnxn=lim1+exn2exn=22=1.
( car n→+∞limexn=e0=1 ; la fonction exp est continue en 0)
4. a Etant donné que la suite (xn)n≥2 est décroissante ;
donc elle est majorée par son premier terme x2
D'où : (∀n≥2) ; xn≤x2
b. On sait que : (∀n≥2) ; 0<xn≤x2
Donc: (∀n≥2) ; 0<(xn)n≤(x2)n
On sait que n→+∞lim0=0 et n→+∞lim(x2)n=0( car 0<x2<1)
Donc n→+∞lim(xn)n=0


