Généralités sur les fonctions

Généralités sur les fonctions numériques

Fonction numérique d'une variable numérique

Introduction 

On considère une voiture qui roule à 100 Km/h.

Veuillez remplir le tableau suivant, afin de capturer la distance parcourue par la voiture en fonction du temps.

Vocabulaire

• La relation qui nous permet de lier chaque élément $x$ de $\mathbb{R}^+$ par un seul élément $y$ de $\mathbb{R}^+$ telle que $y = 100.x$ est appelée fonction numérique de la variable réelle $x$ définie de $\mathbb{R}^+$ vers $\mathbb{R}^+$. On la note $f$, $g$ ou $h$.....
• On opte alors pour la notation suivante : $\begin{array}{l|rcl} f : & \R+ & \longrightarrow & \R+ \\ & x & \longmapsto & 100x \end{array}$
• on appelle $x$ variable
• Dans l'écriture $f(x)=4x$ , si on note $f(x)=y=4x$
  • $x$ est un antécédent de $y$ par $f$
  • $y$ est l'image de $x$ par $f$
  • Par exemple $f(1) = 4$ , donc $1$ est un antécédent de $4$ par $f$. Et, $4$ est l'image de $1$ par la fonction $f$.
• Si l'image de $x$ existe, on dit que la fonction f est définie en $x$ . ( par exemple $-2$ n'a pas d'image).
• Tous les réels $x$ qui ont des images par la fonction $f$ constituent un ensemble appelé ensemble de définition ou domaine de définition, on le note par $D$ ou $Df$. Dans notre exemple $Df = $\mathbb{R}^+$
• $ x \in Df $ équivaut à $ f(x) \in \mathbb{R}$
• $A$ est un ensemble inclus dans $Df$ ( $A \subset Df$) , on dit que la fonction $f$ est définie sur $A$.

Exemples :

Déterminons les domaines de définition des fonctions suivantes :

• $f(x)=\sqrt(x)$
  • $ x \in Df \Leftrightarrow  x \ge 0$ donc $Df = \mathbb{R}^+$.
    On peut aussi écrire $Df = [0, +\infty[$
• $g(x) = \frac{1}{x} $
  • $ x \in Df \Leftrightarrow  x \neq 0$ donc $Df = \mathbb{R}^*$.
    On peut aussi écrire $Df = ]-\infty, 0[ \cup ]0, +\infty[$
• $h(x) = 3x$
  • $ x \in Df \Leftrightarrow  x \in \mathbb{R} $ donc $Df = \mathbb{R}$.

la représentation graphique d'une fonction numérique :

Activité 

On considère la fonction numérique $f$ de variable réelle $x$ définie par $f(x)= 3x + 1$ : Le plan $(P)$ est rapporté au repère $(O,\vec{i},\vec{j})$. On dit que le repère est orthonormé$.

1. Déterminer l'ensemble de définition de la fonction $f$
2. Construire quelques points  $M(x,f(x)) avec x \in Df $ de $(P)$ 

Réponse : 

1. la fonction $f$ est une fonction polynomiale , donc définie sur $\mathbb{R}$.
   Ainsi $Df= \mathbb{R}$.
2. Veuillez consulter le graphe de la fonction $f(x)=3x+1$ ci-dessous : 

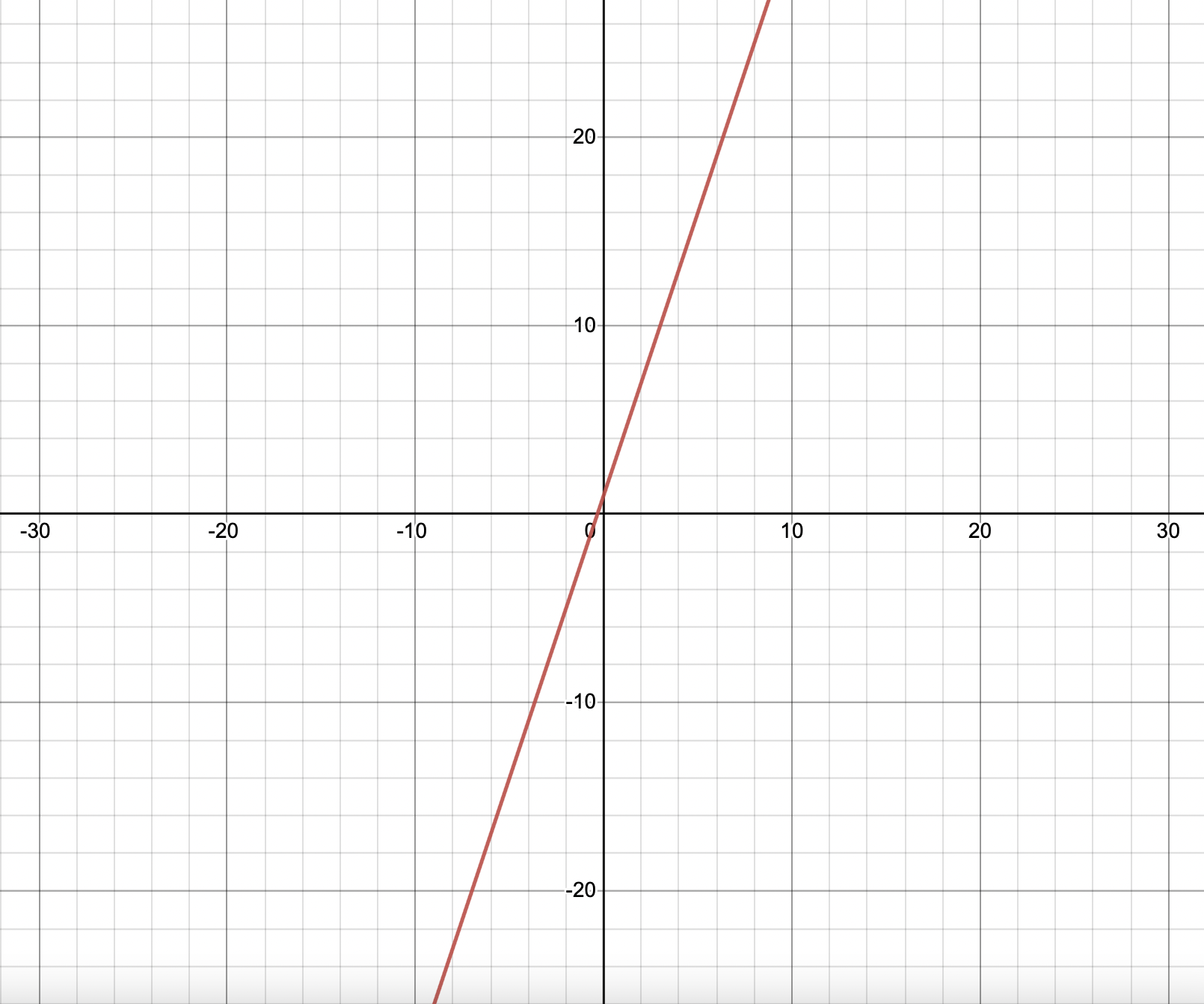
Vocabulaire

Le dessin obtenu s'appelle la représentation graphique de la fonction $f$ dans le repère $(O,\vec{i},\vec{j})$ ( ou la courbe de la fonction $f$), on la note $\mathscr{C}_{f}$.

Définition

Soit $f$ une fonction numérique de la variable réelle $x$ définie sur $Df$ ( $Df \subset R$). 

Le plan $(P)$ est rapporté au repère $(O,\vec{i},\vec{j})$ 

On appelle courbe représentative de la fonction $f$, notée $\mathscr{C}_{f}$, l'ensemble des points $M$ de $(P)$ de coordonnées $(x,f(x))$ ou $x \in Df$.

Un point $M(x,y) \in \mathscr{C}_{f}$ équivaut à $x \in Df$ et $y=f(x)$

la relation $y = f(x)$ s'appelle équation cartésienne de la courbe $\mathscr{C}_{f}$ dans le repère $(O,\vec{i},\vec{j})$ .

لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

النسخة المجانية لكيزاكو:

• ملخصات الدروس غير محدودة
• فيديو مجاني في كل درس
• تمرين مصحح مجاني
• اختبار تفاعلي

إنشاء حساب مجاني