Fiche de cours

Effet d'une force sur la rotation d'un solide

Une force $$\vec{F}$$ a un effet sur la rotation d'un solide pouvant tourner autour d'un axe fixe $$(\Delta)$$ si la droite d'action de la force $$\vec{F}$$ ne coupe pas l'axe de rotation et n'est pas parallèle à cet axe

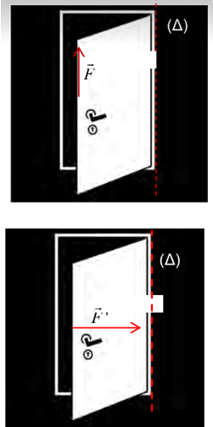
Doc.1 - lac forces $$\vec{F}$$ et $$\vec{F}$$ ' sont sans effet sur la rotation de la porte

Moment d'une force par rapport à un axe

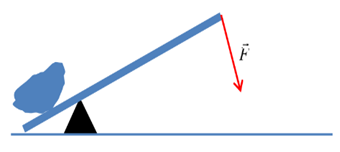
Doc.2 - la force $$\vec{F}$$ permettant de soulever la masse a une intensité d'autant plus faible que la distance $$\mathrm{OA}$$ est grande

تعريف

Le moment d'une force $$\vec{F}$$ par rapport à un axe fixe perpendiculaire à la droite d'action do rette force est le produit de l'intensité de la force $$\vec{F}$$ ef la distance $$\mathrm{d}$$ de sa droite d'action à l'axe $$(\Delta): \boldsymbol{M}_{\Delta}(\vec{F})=\pm F . d$$ L'unité du moment d'une force dans le système international est : N.m.

Le moment d'une force est compté positivement s'il tend à faire tourner le solide dans le sens positif arbitrairement choisi, négativement dans le cas contraire.

$$\text { Doc.3 }-\mathrm{M}_{\Delta}(\vec{F})=+\mathrm{F} . \mathrm{d}$$

 

تطبيق

Une force d'intensité $$8 \mathrm{~N}$$ est représentée par le vecteur $$\overrightarrow{A B}$$ base d'un triangle équilatéral de $$12 \mathrm{~cm}$$ de côté, dont le troisième sommet est la projection sur le plan de la figure de l'axe de rotation. Calculer le moment de cette force par rapport à l'axe passant par $$O$$

$$\text { Doc.4 - M }(\vec{F})=-\mathrm{F} \cdot \mathrm{d}$$

équilibre d'un solide mobile autour d'un axe fixe

Théorème des moments

Lorsqu'un solide susceptible de tourner autour d'un axe fixe $$(\Delta)$$ est en équilibre, la somme algébrique des moments par rapport à $$(\Delta)$$ des forces appliquées est nulle:

$$\sum M_{/ \Delta}\left(\overrightarrow{F^{\prime}}\right)=0$$

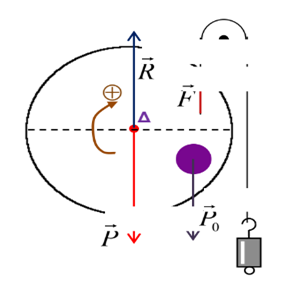
Doc. 4 - équilibre d'un disque sous l'action de plusieurs forces: la somme algébrique des moments de ces forces est nulle.

 

لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

النسخة المجانية لكيزاكو:
  • ملخصات الدروس غير محدودة
  • فيديو مجاني في كل درس
  • تمرين مصحح مجاني
  • اختبار تفاعلي
إنشاء حساب مجاني
Signaler une erreur
Équilibre d'un solide en rotation autour d'un axe fixe
Sommaire du cours
Signaler une erreur