الذبذبات الحرة في دارة RLC متوالية

RLC الكهرباء الدارة متوالية

رابط المشاهدة على يوتيوب: https://youtu.be/0ye-lLUY3sM

تفريغ مكثف في وشيعة

الكهرباء الذبذبات الحرة في دارة المتوالية شرح الدرس الجزء الاول

المتوالية RLC

[KGVID]https://kezakoo.com/wp-content/uploads/2017/11/الثانية-باك-علوم-فيزيائية-_-الكهرباء-الذبذبات-الحرة-في-دارة-RLC-المتوالية-شرح-الدرس-الجزء-الاول.mp4[/KGVID]

رابط المشاهدة على يوتيوب: https://youtu.be/BDja-D_VHdQ

• النتائج:

• الاستثمار:

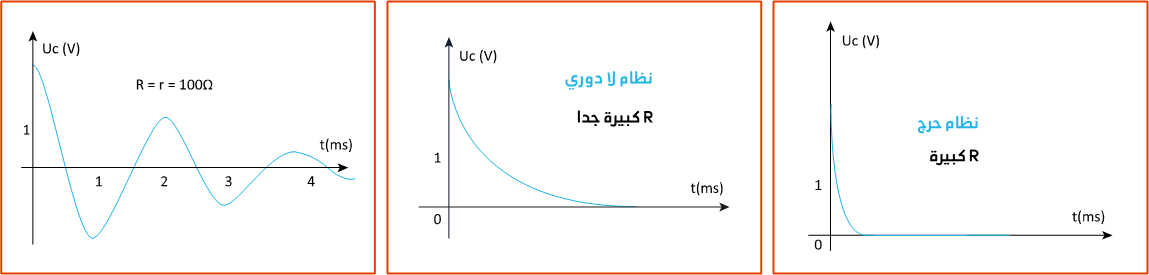
1 – يمثل الرسم التذبذبي الممثل باللون الأزرق في الشكل (2) نموذجا للمنحنى المحصل عليه بالنسبة r’ = 0
1 – 1 – كيف يتغير وسع التوتر (Uc(t ؟ هل(Uc(t دالة دورية ؟
عند وضع K في الموضع (1) يشحن المكثف وعند وضعه في الموضع (2) نحصل على دارة RLC متوالية حيث في هذه الحالة يفرغ المكثف في الوشيعة.
ويكون التوتر (Uc(t بين مربطي المكثف متناوبا . (Uc(t ليست بدالة دورية.
- وسع التوتر (Uc(t يتناقص مع الزمن t نقول أن التذبذبات مخمدة.
بما أن الذبذبات تتم دون أن نزود الدارة RLC بالطاقة غير الطاقة المخزونة في المكثف , نقول أن الذبذبات حرة.

• خلاصة:

يؤدي تفريغ مكثف,  مشحون,  في وشيعة دارة RLC  متوالية ,  إلى ظهور تذبذبات حرة ومخمدة.
نقول أن الدارة RLC  المتوالية تكون متذبذبا كهربائيا حرا ومخمدا.

• أنظمة الذبذبات الحرة:

1 – 2 – نسمي شبه الدور T  المدة الزمنية الفاصلة بين قيمتين قصويتين متتاليين للتوتر  (Uc(t  . عين مبيانيا T  من خلال المبيان يمكن أن نعين شبه الدور وهو المدة الزمنية الفاصلة بين قيمتين قصويتين متتاليتين للتوتر (Uc(t  .

• تعريف بشبه الدور T:

نسمي شبه الدور T  المدة الزمنية الفاصلة بين قيمتين قصويتين متتاليين للتوتر (Uc(t  .

2 – ما ثأثير المقاومة R  على :
2 – 1 – وسع التذبذبات ؟

عندما نغير المقاومة الكلية للدارة يتغير وسع الذبذبات.

2 – 2 شبه الدور T  ؟

بالنسبة لقيم المقاومة صغيرة جدا يلاحظ أن شبه الدور لا يتعلق بقيمة R

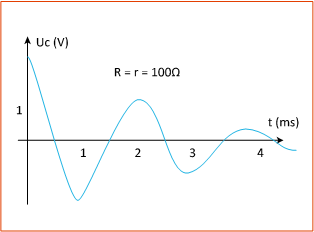
3 – عندما تاخد المقاومة ’r قيمة كبيرة جدا :  هل التوتر (Uc(t المعاين تذبذبي ؟

عندما تأخد R  قيم كبيرة جدا (Uc(t  توتر غير تذبذبي أي أن الذبذبات تزول يكون لدينا خمود مهم.

4 – حسب قيم المقاومة الكلية R  للدارة RLC  يلاحظ تجربيا وجود نظامين للذبذبات :  نظام شبه دوري و نظام لا دوري.

تعرف على هاذين النظامين من خلال الشكل 2

النظام شبه الدوري يحدث إذا كانت قيمة المقاومة  R  صغيرة.
النظام لا دوري عندما تكون R  كبيرة جدا حيث تزول الذبذبات نظرا لوجود خمود مهم.

5 – نضبط من جديد ’r  على القيمة 0

في المرحلة أولى نأخد L = 11mH  و C = 1µF  ونقيس شبه الدور T

في المرحلة ثانية :  نأخد L = 11mH  و C = 0.22µF  ونقيس T

هل يتعلق شبه الدور بكل من L  و C  ؟

نعم يتعلق شبه الدور بقيم  L  و C  ولا يتعلق بقيم R

• أنظمة الذبذبات الحرة:

حسب مقاومة الدارة RLC  نحصل على ثلاثة أنظمة:

أ – نظام شبه دوري :

R  صغيرة نحصل على ذبذبات يتناقص وسعها تدرجيا مع الزمن

ب – نظام لا دوري:</h5/> R  كبيرة جدا = تزول الذبذبات نظرا لوجود خمود مهم و نسمي هذا النظام نظام لا دوري

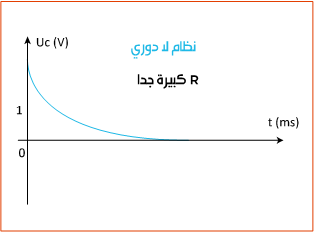
ج – نظام حرج:

في الذبذبات الحرة توجد قيمة معينة للمقاومة نرمز لها ب Rc  وتسمى مقاومة حرجة وهي مقاومة تفصل بين النظام شبه دوري و النظام اللا دوري ونسمي النظام في هذه الحالة بالنظام الحرج وفي هذه الحالة بالنظام الحرج وفي هذه الحالة يرجع التوتر (Uc(t إلى صفر بسرعة ودون تذبذب وتتعلق Rc  ب C  و L.

2 – المعادلة التفاضلية لدارة RLC  متوالية:  

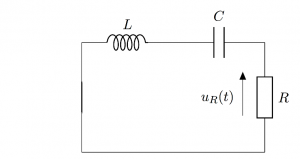
نعتبر الدارة المتوالية الممثلة في الشكل جانبه :

نطبق قانون إضافية التوترات بين F  و D  فنجد:

المعادلة التفاضلية لدارة RLC  متوالية التي يحققها التوتر (Uc(t بين مربطي المكثف هي :  

يعبر المقدار 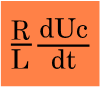  عن ظاهرة خمود الذبذبات،  و يحدد حسب قيم R  نظام هذه الذبذبات.

 

الذبذبات الغير المخمدة في دارة مثالية LC