RLC libre

Oscillations libres d'un circuit LC

Montage d’un circuit LC

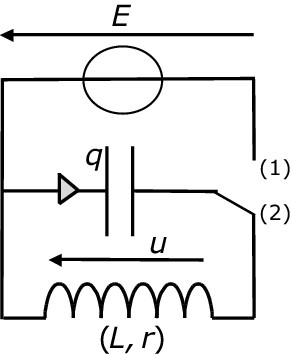
Equation différentielle

$$U_{C}+U_{L}=0$$
$$U_{C}+L \cdot \frac{d i}{d t}=0$$
$$U_{C}+L C \cdot \frac{d^{2} U_{C}}{d t^{2}}=0$$
$$\frac{1}{L C} \cdot U_{C}+\frac{d^{2} U_{C}}{d t^{2}}=0$$

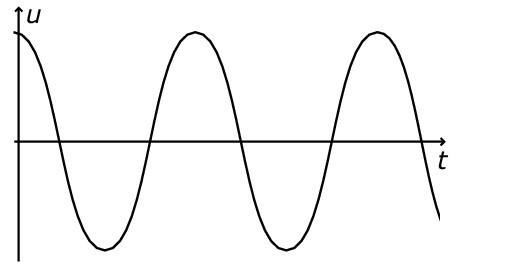
Equation horaire

La solution de l’équation différentielle $$\frac{1}{L C}+\frac{d^{2} U_{C}}{d t^{2}}=0$$ s’écrit sous forme :
$$U_{C}(t)=U_{C \max } \cdot \cos \left(\frac{2 \pi}{T_{0}} t+\varphi\right)$$
$$U_{C}(t)$$ : Tension aux bornes du condensateur en (V)
$$U_{C \max }$$ : Amplitude des oscillations (c'est l'élongation maximale) en (V)
$$T_{0}$$ : La période propre des oscillations.
$$\varphi$$ : La phase du mouvement à l'instant t=0 en (rad).
La dérivée de la solution est :
$$\frac{d U_{C}}{d t}=-U_{C \max } \cdot \frac{2 \pi}{T_{0}} \sin \left(\frac{2 \pi}{T_{0}} t+\varphi\right)$$
Et sa dérivée seconde est :
$$\frac{d^{2} U_{C}}{d t^{2}}=-\frac{4 \pi^{2}}{T_{0}^{2}} \cdot U_{C \max } \cdot \cos \left(\frac{2 \pi}{T_{0}} t+\varphi\right)=-\frac{4 \pi^{2}}{T_{0}^{2}} \cdot U_{C}$$
En remplaçant dans l’équation différentielle, on obtient
$$-\frac{4 \pi^{2}}{T_{0}^{2}} \cdot U_{C}+\frac{1}{L C} U_{C}=0$$
Alors :
$$\frac{1}{L C} U_{C}=\frac{4 \pi^{2}}{T_{0}^{2}} \cdot U_{C}$$
D’où $$T_{0}=2 \pi \sqrt{L C}$$

La période propre

Dimension de la période propre

On a $$T_{0}=2 \pi \sqrt{L C}$$
$$[T]=([L] .[C])^{1 / 2}$$
$$U_{L}=L \frac{d i}{d t} \Rightarrow[U]=[L] \cdot \frac{[I]}{[T]}$$
$$[L]=[U] \cdot \frac{[T]}{[I]}$$
$$q=C . U \Longrightarrow[I] \cdot[T]=[C] .[U]$$
$$[C]=\frac{[I][T]}{[U]}$$
$$\left[T_{0}\right]=\left([U] \cdot \frac{[T]}{[I]} \times \frac{[I][T]}{[U]}\right)^{1 / 2}=\left([T]^{2}\right)^{1 / 2}=[T]$$
Donc la période propre $$T_{0}$$ a la dimension d’un temps et son unité est la seconde.

Bilan énergétique

On tient à préciser que l’énergie emmagasinée dans le condensateur est une énergie électrique ainsi que l’énergie emmagasinée dans la bobine est une énergie magnétique, l’énergie totale résultante est la somme des deux énergies

Conservation de l’énergie

Pour montrer que l’énergie se conserve, il faut trouver que $$\frac{d E_{t}}{d t}=0$$ avec
$$E_{t}=E_{e}+E_{m}$$
On a $$E_{e}=\frac{1}{2} \cdot C \cdot U_{c}^{2}$$ et $$E_{m}=\frac{1}{2} \cdot L \cdot i^{2}=\frac{1}{2} . L . C^{2}\left(\frac{d U_{C}}{d t}\right)^{2}$$
Alors $$E_{t}=\frac{1}{2} \cdot C . U_{c}^{2}+\frac{1}{2} . L . C^{2}\left(\frac{d U_{C}}{d t}\right)^{2}$$
D’où $$\frac{d E_{t}}{d t}=\frac{1}{2} \cdot L . C^{2} \cdot 2 \cdot \frac{d U_{C}}{d t} \cdot \frac{d^{2} U_{c}}{d t^{2}}+\frac{1}{2} . \text { C. } 2 . U_{c} \cdot \frac{d U_{c}}{d t}$$
$$\frac{d E_{t}}{d t}=C \cdot \frac{d U_{c}}{d t}\left(L . C \cdot \frac{d^{2} U_{c}}{d t^{2}}+U_{C}\right)$$

On sait déjà d’après l’équation différentielle que
$$\frac{1}{L C}+\frac{d^{2} U_{C}}{d t^{2}}=0$$
On peut conclure que : $$\frac{d E_{t}}{d t}=0$$ alors l’énergie se conserve

La courbe énergétique

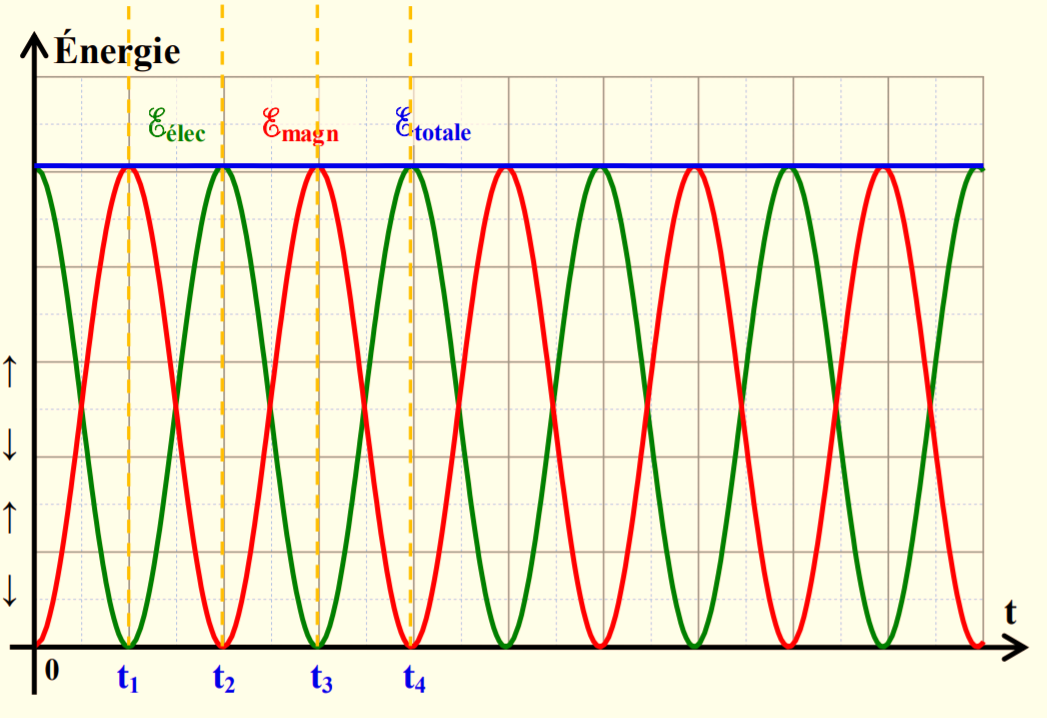
Oscillations libres d'un circuit RLC

لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

النسخة المجانية لكيزاكو:

• ملخصات الدروس غير محدودة
• فيديو مجاني في كل درس
• تمرين مصحح مجاني
• اختبار تفاعلي

إنشاء حساب مجاني