Régime alternatif sinusoïdal
On a vu précédemment que le circuit (R, L, C) en série forme un oscillateur électrique amorti. Lorsqu’on ajoute, en série, un générateur électrique au circuit qui l’alimente d’une tension alternative sinusoïdale, c’est à dire qu’il impose un régime alternatif sinusoïdal à l’oscillateur ; on obtient un régime sinusoïdal forcé
Courant alternatif sinusoïdal
L’intensité du courant alternatif sinusoïdal est une fonction du temps qui s’écrit sous la forme :
$$i(t)=I_{m} \cos \left(\omega t+\varphi_{i}\right)$$
Avec :
$$I_{m}$$ : Amplitude du courant / l’intensité maximale du courant en (A)
$$\omega$$ : pulsation du courant électrique telle que $$\omega=\frac{2 \pi}{T}=2 \pi N$$son unité (rad/s)
$$\omega t+\varphi_{i}$$ : La phase de u(t) à l’instant t sont unité dans le (S.I) est (rad)
$$\varphi_{i}$$ : La phase à l’origine (à t = 0) en (Rad) et on la détermine à partir des conditions initiales
Tension alternative sinusoïdale
La tension alternative sinusoïdale est une fonction du temps qui s’écrit sous la forme :
$$u(t)=U_{m} \cos \left(\omega t+\varphi_{u}\right)$$
Avec :
$$U_{m}$$ : Amplitude de la tension u(t) / la tension maximale de u(t) en (V)
$$\omega$$ : pulsation du courant électrique telle que $$\omega=\frac{2 \pi}{T}=2 \pi N$$ son unité (rad/s)
$$\omega t+\varphi_{u}$$ : La phase de u(t) à l’instant t sont unité dans le (S.I) est (rad)
$$\varphi_{u}$$ : La phase à l’origine (à t = 0) en (Rad) et on la détermine à partir des conditions initiales
Valeurs efficaces
Intensité efficace du courant
On note l’intensité efficace d’un courant alternatif sinusoïdal par I et on l’exprime par la relation suivante :
$$I=\frac{I_{m}}{\sqrt{2}}$$
L’ampèremètre utilisé en courant alternatif indique la valeur de l’intensité efficace.
La tension efficace U
On note la tension efficace d’une tension alternative sinusoïdale par U et on l’exprime par la relation suivante :
$$U=\frac{U_{m}}{\sqrt{2}}$$
Le voltmètre utilisé en courant alternatif indique la valeur efficace de la tension.
Déphasage et Décalage horaire entre deux courbes sinusoïdales
Notion de phase
On considère deux grandeurs alternatives sinusoïdales :
$$i(t)=I_{m} \cos \left(\omega t+\varphi_{i}\right) \text { et } u(t)=U_{m} \cos \left(\omega t+\varphi_{u}\right)$$
On appelle la phase de u(t) par rapport à i(t) : $$\varphi_{u / i}=\varphi_{u}-\varphi_{i}$$\ et la phase de i(t) par rapport à u(t) : $$\varphi_{i / u}=\varphi_{i}-\varphi_{u}$$
$$\varphi_{u / i} \text { et } \varphi_{i / u}$$ mesure l’avance et la retard de chaque fonction par rapport à l’autre.
$$\varphi_{u / i}>0$$ : on dit que u(t) est en avance sur i(t)
$$\varphi_{u / i}<0$$ : u(t) est en retard sur i(t)
$$\varphi_{u / i}=\frac{\pi}{2}$$ : on dit que u(t) et i(t) sont en quadrature de phase
$$\varphi_{u / i}=\pi$$ on dit que u(t) et i(t) sont en en opposition phase
$$\varphi_{u / i}=0$$ u(t) et i(t) sont en phase.
مثال
On considère les deux tensions alternatives sinusoïdales représentées par les deux courbes suivantes :
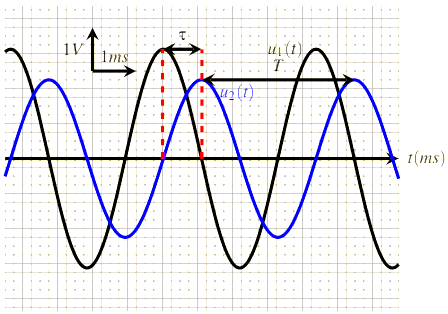
Pour déterminer la valeur de la phase, on prend $$\varphi_{i}=0 \text { et } \varphi_{u / i}=\varphi_{u}$$\
La relation devient :
$$i(t)=I_{m} \cos (\omega t) \text { et } u(t)=U_{m} \cos \left(\omega t+\varphi_{u / i}\right)$$
$$u(t)=U_{m} \cos \left(\omega\left(t+\frac{\varphi_{u / i}}{\omega}\right)\right)$$
$$\frac{\varphi_{u / i}}{\omega}=\tau$$
On appelle $$\tau$$ le décalage horaire entre u(t) et i(t), la mesure directe de $$\tau$$ à l’oscilloscope permet d’évaluer la valeur absolue de la phase $$\varphi_{u}$$
$$\left|\varphi_{u / i}\right|=\frac{2 \pi}{T} \cdot \tau$$
L’expression de l’intensité du courant alternatif sinusoïdal dans un condensateur de capacité C
On sait que l’intensité du courant qui traverse le condensateur est :
$$i(t)=C \cdot \frac{d U_{c}}{d t}$$
$$i(t)=-C U_{c} \omega \sqrt{2} \sin (\omega t)$$
$$i(t)=C U_{c} \omega \sqrt{2} \cos \left(\omega t+\frac{\pi}{2}\right)$$
L’intensité efficace I du courant est $$I=C U_{c} \omega$$, d’où la tension efficace entre les bornes du condensateur est :
$$U_{c}=\frac{I}{C \omega}$$
L’expression de la tension alternative sinusoïdale aux bornes d’une bobine
On a $$i(t)=I_{m} \sqrt{2} \cos (\omega t)$$
$$U_{L}(t)=L \cdot \frac{d i}{d t}$$
$$U_{L}(t)=-L I \omega \sqrt{2} \sin (\omega t)$$
$$U_{L}(t)=L I \omega \sqrt{2} \cos \left(\omega t+\frac{\pi}{2}\right)$$
D’où la tension efficace U_L aux bornes d’une bobine est :
$$U_{L}=L I \omega$$
Étude expérimentale d’un circuit RLC série en régime alternatif sinusoïdal
Oscillations forcées dans un circuit RLC série
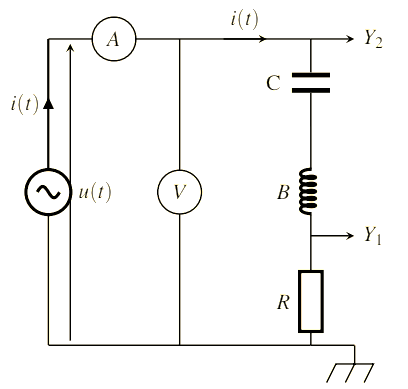
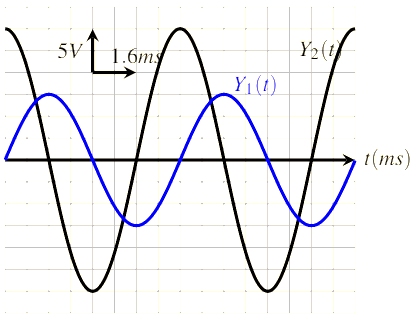
Le générateur GBF délivre au circuit (R, L, C) en série une tension alternative sinusoïdale :
$$u(t)=U_{m} \cos \left(\omega t+\varphi_{u / i}\right)$$
Il apparaît dans le circuit un courant électrique d’intensité $$i(t)=I_{m} \cos (\omega t)$$, représente le courant i(t) la réponse du circuit (R, L, C) à l’excitation qui est imposée par le générateur de base fréquence.
On appelle le circuit (R, L, C) série le résonateur et le générateur GBF excitateur Les deux entrées $$Y_{1} \text { et } Y_{2}$$ de l’oscilloscope, nous permet de visualiser la tension $$U_{R}(t)$$ aux bornes du conducteur ohmique et la tension u(t) aux bornes du circuit (R, L, C)
Impédance d’un circuit RLC
Reprenons le montage précédent, pour une fréquence fixée de la tension, on fait varier la tension efficace U du générateur. On mesure les valeurs de U et I et on relève le déphasage $$\varphi_{u / i} $$, pour le déphasage, on constate qu’il reste constant quelque soit la tension efficace U et pour I et U on les regroupe dans le tableau suivant :

On constate que U et I sont inversement proportionnelle et que U = Z.I avec Z un facteur de proportionnalité, on l’appelle l’impédance du circuit. Qui a une dimension de la résistance $$\Omega$$
تعريف
On appelle Z l’impédance du circuit, son expression est :
$$Z=\frac{I_{m}}{U_{m}}=\frac{U}{I}$$
Son unité dans le système internationale est $$\Omega$$
Influence de la fréquence
On fait varier la fréquence d’un circuit (R, L, C) et on observe que le déphasage change et aussi l’impédance Z, donc l’impédance Z dépend de la fréquence du circuit.
Phénomène de résonance électrique
لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

- ملخصات الدروس غير محدودة
- فيديو مجاني في كل درس
- تمرين مصحح مجاني
- اختبار تفاعلي