La modulation d’amplitude
Une information - un signal
Le principe de la modulation d’amplitude consiste à modifier l’amplitude d’une onde électromagnétique de haute fréquence (HF), appelée onde porteuse p(t), par un signal électrique de basse fréquence (BF), appelé signal modulant, contenant l’information s(t) à transmettre, cette opération est réalisée par un modulateur
Le signal modulant
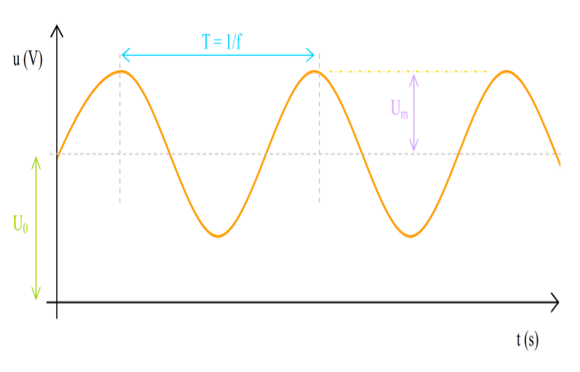
Le signal modulant us est un signal de basse fréquence fs d’amplitude
$$\mathrm{S}(\mathrm{t})=\mathrm{S}_{\mathrm{m}} \cos \left(2 \pi \mathrm{f}_{\mathrm{s}} \mathrm{t}\right)$$
Le signal porteur
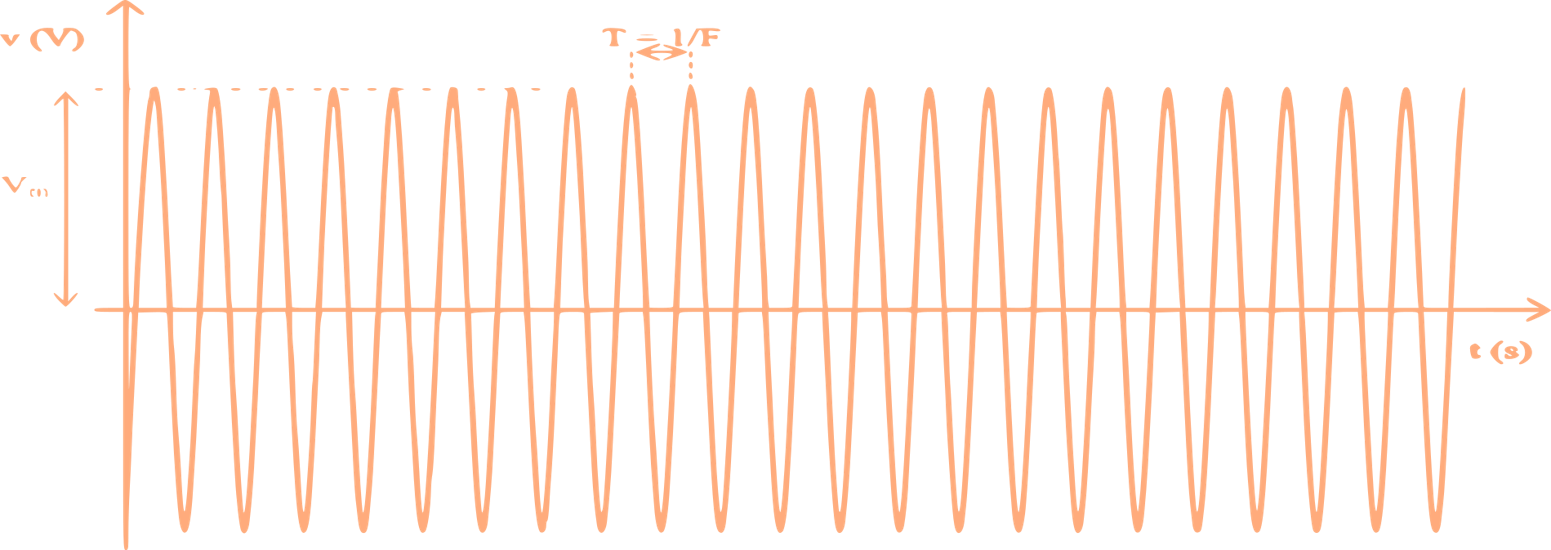
La porteuse est une onde sinusoïdale de haute fréquence P(t) et d’amplitude constante
$$\mathrm{P}(\mathrm{t})=\mathrm{p}_{\mathrm{m}} \cos \left(2 \pi \mathrm{f}_{\mathrm{p}} \mathrm{t}\right)$$
La modulation
La modulation d’amplitude consiste à modifier l’amplitude d’une onde porteuse de fréquence très élevée par le signal à transmettre auquel on ajoute une tension continue.
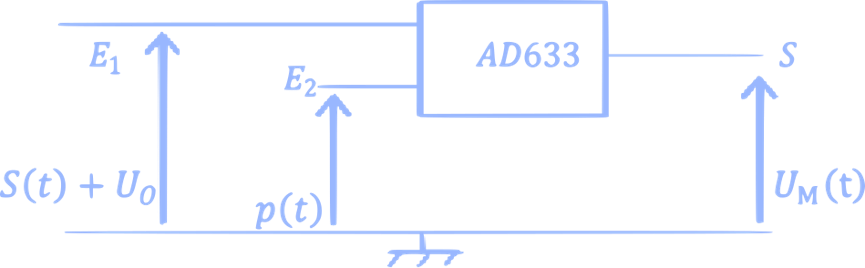
Pour moduler l’amplitude de l’onde porteuse P(t), on utilise un multiplieur X (circuit intégré AD633) qui réalise le produit du signal porteur p(t) par le signal modulant $$\left[\mathrm{s}(\mathrm{t})+U_{0}\right]$$, signal informatif décalé. Avec : s(t) : représente signal à transmettre (information) et $$U_{0}$$ : une tension continue nommée tension de décalage.
Le signal modulé
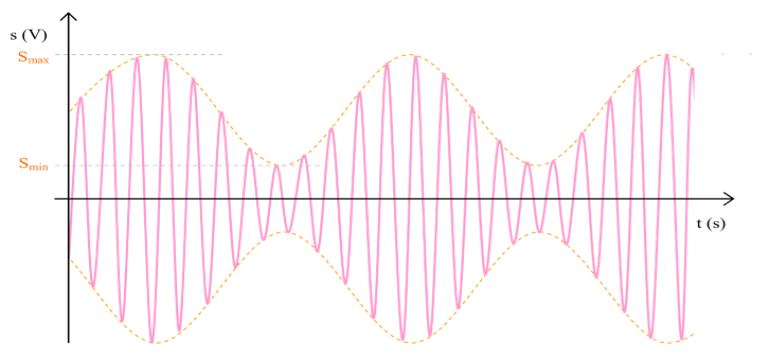
On doit ajouter une tension de décalage $$U_{0}$$ au signal modulant avant de moduler la porteuse, la formule du signal modulé
L’amplitude de la tension modulée Um(t) est une fonction affine de la tension modulante Us(t), elle s’écrit : Um(t)=a[us(t)+b]. Elle en reproduit les variations au cours du temps.
Et $$\mathrm{U}_{\mathrm{s}}(\mathrm{t})=\mathrm{A}\left[\mathrm{m} \cos \left(2 \pi \mathrm{f}_{\mathrm{s}} \mathrm{t}\right)+1\right]$$ avec :
$$\mathrm{m}=\frac{\mathrm{S}_{\mathrm{m}}}{\mathrm{U}_{\mathrm{o}}}$$
et $$\mathrm{A}=\mathrm{K} . \mathrm{P}_{\mathrm{m}} . \mathrm{U}_{0}$$
Le taux de modulation
On appelle taux de modulation le rapport entre la tension du signal modulant, et la tension de la porteuse, on le calcule à travers deux relations :
$$\mathrm{m}=\frac{\mathrm{S}_{\mathrm{m}}}{\mathrm{U}_{0}}$$
$$\mathrm{m}=\frac{\mathrm{U}_{\max }-\mathrm{U}_{\min }}{\mathrm{U}_{\max }+\mathrm{U}_{\min }}$$
La qualité de la modulation
Pour obtenir une tension modulée de bonne qualité, il faut appliquer une tension $$U_{o}$$, appelée tension de décalage, supérieure à l’amplitude de la tension modulante : $$U_{0}>S_{m}$$
Pour obtenir une tension modulée de bonne qualité, il faut que la fréquence de la porteuse $$f_{\mathrm{p}}$$ soit largement supérieure à celle de la tension modulante $$f_{\mathrm{s}}: f_{\mathrm{p}}>f_{\mathrm{s}}$$
Spectre des fréquences
Le spectre de fréquences du signal modulé est un graphe présentant l'amplitude de chaque composante sinusoïdale du signal.
On a :
$\begin{aligned}\mathrm{us(t)}&=\mathrm{A} \cdot(1+\mathrm{A} \cdot \mathrm{m} \cdot \cos (2 \cdot \pi \cdot \mathrm{f_s} \cdot t)) \cdot \cos (2 \cdot \pi \cdot \mathrm{F_p} \cdot \mathrm{t})\\ &=\mathrm{A} \cdot \cos (2 \cdot \pi \cdot \mathrm{F_p} \cdot \mathrm{t})+\mathrm{A} \cdot \mathrm{m} \cdot \cos (2 \cdot \pi \cdot f \mathrm{f_s} \cdot \mathrm{t}) \cdot \cos (2 \cdot \pi \cdot \mathrm{F_p} \cdot t)\end{aligned}$
On sait que $\quad 2 \cdot \cos (a) \cdot \cos (b)=\cos (a+b)+\cos (a-b)$
$\mathrm{u s(t)=A \cdot \cos \left(2 \cdot \pi \cdot F_p \cdot t\right)+\frac{A \cdot m}{2} \cdot \cos \left(2 \cdot \pi \cdot\left(F_p-f_s\right) \cdot t\right)} \\ +\mathrm{\frac{A \cdot m}{2} \cdot \cos \left(2 \cdot \pi \cdot\left(F_p+f_s\right) \cdot t\right)}$
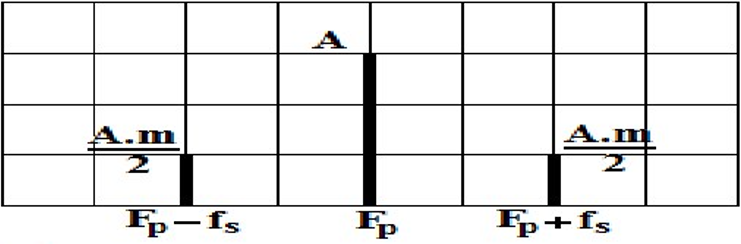
Conclusion : la tension modulée est la somme de trois tensions sinusoïdales avec des fréquences différentes
| La fonction | $A \cdot \cos \left(2 \cdot \pi \cdot F_p \cdot t\right)$ | $\frac{A \cdot m}{2} \cdot \cos \left(2 \cdot \pi \cdot\left(F_p-f_s\right) \cdot t\right)$ | $\frac{A \cdot m}{2} \cdot \cos \left(2 \cdot \pi \cdot\left(F_p+f_s\right) \cdot t\right)$ |
| Amplitude | $A$ | $\frac{A \cdot m}{2}$ | $\frac{A \cdot m}{2}$ |
| Fréquence | $F_p$ | $F_p-f_s$ | $F_p+f_s$ |
La démodulation
لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

- ملخصات الدروس غير محدودة
- فيديو مجاني في كل درس
- تمرين مصحح مجاني
- اختبار تفاعلي