Condensateur – Dipôle RC

Les composantes d’un circuit RC

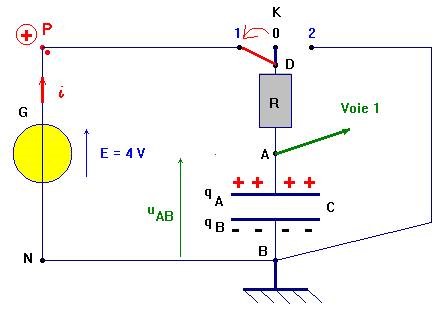
Montage d’un circuit RC

Le générateur utilisé est un générateur de courant qui délivre une tension constante E, en temps t = 0 s, on bascule l'interrupteur sur la position 1 et on charge le condensateur.
Au cours de la charge, l'armature A se charge positivement. Elle présente un déficit d’électrons $$\mathrm{q}_{\mathrm{A}}>0$$ et l'armature B se charge négativement, elle présente un excès d'électrons : $$\mathrm{q}_{\mathrm{B}}<0$$.
Par définition, la quantité $$\mathrm{q}_{\mathrm{A}}=-\mathrm{q}_{\mathrm{B}}$$ représente la charge du condensateur, c’est une grandeur positive. Elle s’exprime en Coulomb C, et on l’appelle aussi ; quantité d’électricité emmagasinée.
Une tension $$\mathrm{U}_{\mathrm{AB}}$$ apparaît entre les plaques A et B lorsque le condensateur se charge, lorsque le condensateur est chargé, la valeur de l'intensité s'annule et la tension $$\mathrm{U}_{\mathrm{AB}}$$ prend sa valeur maximale.

La résistance

Association de deux résistances

Association en série :

La valeur R d’une résistance équivalente à un ensemble des résistances de valeurs $$\mathrm{R}_{1}, \mathrm{R}_{2}, \ldots, \mathrm{R}_{n}$$, montés en série est : $$\mathrm{R}=\mathrm{R}_{1}+\mathrm{R}_{2}+\ldots \ldots+\mathrm{R}_{\mathrm{n}}$$

Association en parallèle :

La valeur R d’une résistance équivalente à un ensemble des résistances de valeurs $$\mathrm{R}_{1}, \mathrm{R}_{2}, \ldots, \mathrm{R}_{\mathrm{n}}$$ montés en parallèle est
$$\frac{1}{\mathrm{R}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}+\frac{1}{\mathrm{R}_{3}}+\ldots \ldots \ldots+\frac{1}{\mathrm{R}_{\mathrm{n}}}$$

Condensateur

Les condensateurs diffèrent par leur géométrie, puisque les armateurs peuvent avoir plusieurs formes géométriques (planes, cylindriques ...).

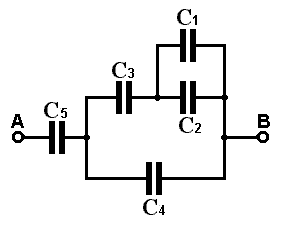
Association de deux condensateurs

Association en série :

La capacité C d’un condensateur équivalent à un ensemble des condensateurs de capacités $$C_{1}, C_{2}, \ldots, C_{n}$$ montés en série est
$$\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_{1}}+\frac{1}{\mathrm{C}_{2}}+\frac{1}{\mathrm{C}_{3}}+\ldots \ldots \ldots+\frac{1}{\mathrm{C}_{\mathrm{n}}}$$

Association en parallèle :

La capacité C d’un condensateur équivalent à un ensemble des condensateurs de capacités $$\mathrm{C}_{1}, \mathrm{C}_{2}, \ldots, \mathrm{C}_{\mathrm{n}}$$ montés en parallèle est :
$$\mathrm{C}=\mathrm{C}_{1}+\mathrm{C}_{2}+\ldots \ldots+\mathrm{C}_{\mathrm{n}}$$

Relation charge-tension

Relation courant-charge

Relation courant-tension

La charge d’un condensateur

Montage

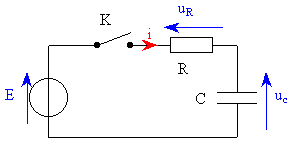
On réalise le montage expérimental représenté sur la figure 1 comprenant :
- Un générateur de tension continue de force électromotrice E
- Un condensateur de capacité C initialement déchargé
- Un conducteur ohmique de résistance R
- Un interrupteur K
Pour charger le condensateur à l’instant t = 0, on ferme l’interrupteur K

Equation différentielle

Equation différentielle de la tension
On a selon la loi d’additivité des tenions
$$\mathrm{U}_{\mathrm{C}}+\mathrm{U}_{\mathrm{R}}=\mathrm{E}$$
$$\mathrm{U}_{\mathrm{C}}+\mathrm{R} \cdot \mathrm{i}=\mathrm{E}$$
$$\mathrm{U}_{\mathrm{C}}+\mathrm{R} \cdot \frac{\mathrm{dq}}{\mathrm{dt}}=\mathrm{E}$$
$$\mathrm{U}_{\mathrm{C}}+\mathrm{RC} \cdot \frac{\mathrm{d} \mathrm{U}_{\mathrm{C}}}{\mathrm{dt}}=\mathrm{E}$$

Equation horaire

On a la solution de l’équation différentielle est : $$\mathrm{U}_{\mathrm{C}}(\mathrm{t})=\mathrm{Ae}^{-\frac{\mathrm{t}}{\tau}}+\mathrm{B}$$
$$\frac{d \mathrm{U}_{\mathrm{C}}}{d \mathrm{t}}=\mathrm{A}\left(-\frac{1}{\tau} \mathrm{e}^{-\frac{\mathrm{t}}{\tau}}\right)=-\frac{\mathrm{A}}{\tau} \mathrm{e}^{-\frac{\mathrm{t}}{\tau}}$$
Alors :
$$\mathrm{U}_{\mathrm{C}}+\mathrm{RC} \cdot \frac{\mathrm{dU}_{\mathrm{C}}}{\mathrm{dt}}=\mathrm{E}$$
Devient
$$\mathrm{Ae}^{-\frac{\mathrm{t}}{\tau}}+\mathrm{B}+\mathrm{RC}\left(-\frac{\mathrm{A}}{\tau} \mathrm{e}^{-\frac{\mathrm{t}}{\tau}}\right)=\mathrm{E}$$
$$\mathrm{Ae}^{-\frac{\mathrm{t}}{\tau}}\left(1-\frac{\mathrm{RC}}{\tau}\right)+\mathrm{B}-\mathrm{E}=0$$
Alors B=E et $$1-\frac{\mathrm{RC}}{\tau}=0 \Rightarrow \tau=\mathrm{RC}$$
On remplace B et \tau dans la solution de l’équation différentielle
$$\mathrm{U}_{\mathrm{C}}(\mathrm{t})=\mathrm{Ae}^{-\frac{\mathrm{t}}{\mathrm{RC}}}+\mathrm{E}$$
Pour trouver la valeur de A, on considère t=0
$$\mathrm{U}_{\mathrm{C}}(0)=\mathrm{Ae}^{0}+\mathrm{E}$$
Alors A=-E
$$\mathrm{U}_{\mathrm{C}}(\mathrm{t})=-\mathrm{Ee}^{-\frac{\mathrm{t}}{\mathrm{RC}}}+\mathrm{E}$$
$$\mathrm{U}_{\mathrm{C}}(\mathrm{t})=\mathrm{E}\left(1-\mathrm{e}^{-\frac{\mathrm{t}}{\mathrm{RC}}}\right)$$

Représentation graphique

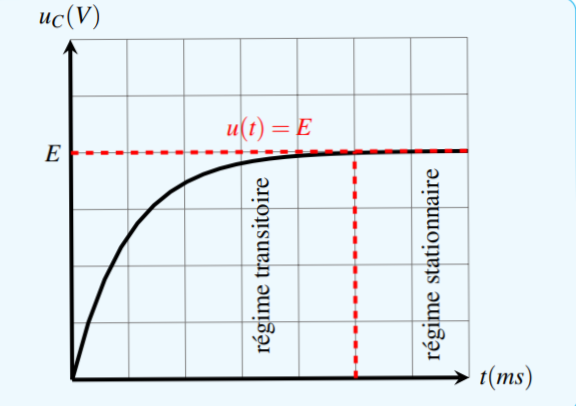
Dans la représentation graphique de la charge d’un condensateur on trouve deux régimes, un régime transitoire dans lequel la valeur de la tension aux bornes du condensateur augmente d’une manière exponentielle, ainsi qu’un régime permanant dans lequel la valeur de la tension aux bornes du condensateur atteint une valeur limite constante égale à E

Détermination de la constante du temps

On a $$\mathrm{U}_{\mathrm{C}}(\mathrm{t})=\mathrm{E}\left(1-\mathrm{e}^{-\frac{\mathrm{t}}{\tau}}\right)$$
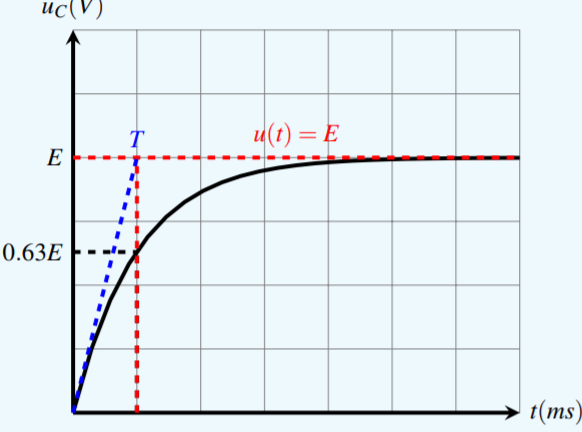
À l’instant $$\mathrm{t}=\tau$$ on a $$\mathrm{U}_{\mathrm{C}}(\tau)=\mathrm{E}\left(1-\mathrm{e}^{-\frac{\tau}{\tau}}\right)=0,63 \mathrm{E}=63 \% \mathrm{E}$$
La constante de temps est la durée nécessaire pour que le condensateur atteigne 63 % de sa charge maximale. (Pour que la tension $$\mathrm{U}_{\mathrm{C}}(\mathrm{t})$$ atteigne 63 % de sa valeur maximale).
On peut déterminer graphiquement la constante de temps par deux méthodes :
Méthode 1 :
La projection : On projette la valeur 0,63 E sur la courbe puis sur l’axe des abscisses (l’axe du temps)
Méthode 2 :
La tangente à la courbe à l’instant t =0 : est l’abscisse du point d’intersection entre la tangente à la courbe à l’instant t =0 et l’asymptote horizontale d’équation y = E

La décharge d’un condensateur