Chute verticale d'un solide

Chute verticale d’un solide avec frottement dans un fluide

Forces exercées par le fluide sur le solide en mouvement

Poussée d’Archimède

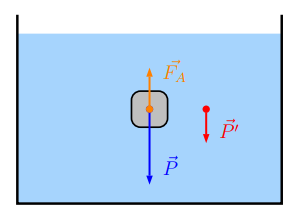
Tout corps totalement ou partiellement immergé dans un fluide (liquide ou gaz) subit une force $$\overrightarrow{F_{A}}$$ appelée poussée d’Archimède qui a les caractéristiques suivantes :
Son point d’application est centre du volume immergé (le point C)
Sa direction est toujours verticale (droite verticale passant par le point C)
Son sens est vers le haut
Son intensité $$F_{A}$$ est égale au poids du fluide déplacé : $$F_{A}=\rho_{f} \cdot V_{f} \cdot g$$ Avec
$$F_{A}$$ : poussée d’Archimède en (N)
$$\rho_{f}$$ : masse volumique du fluide en ($$\text { Kg.m }^{-3}$$)
$$V_{f}$$ : volume du fluide déplace ou volume de la partie immergée du solide en ($$m^{3}$$)
g:\ Intensité du champ de pesanteur en ($$\text { N. } k g^{-1}$$)

Si le solide est totalement immergé alors, le point d’application C est confondu avec G le centre de gravité et $$V_{f}=V_{s}$$\ (volume du solide) donc : $$\overrightarrow{F_{A}}=\rho_{f} \cdot V_{s} \cdot \vec{g}$$

Le poids du corps

Sur Terre, par définition, le poids est l'action exercée par la Terre sur tout objet se trouvant à proximité de sa surface,

Tout objet possédant une masse possède aussi un poids.
Le poids d'un objet est toujours vertical et orienté vers le bas (vers le centre de la Terre).
La valeur du poids ou intensité du poids est souvent appelé, par simplification, poids de l'objet.
Le poids d'un objet s'exprime en Newton de symbole N ou en l'une de ses unités dérivées.
Pour la chute verticale dans un solide, le poids du corps a toujours la même direction de la poussée d’Archimède mais dans un sens inverse.

Force de frottement exercée par le fluide

De façon générale, si un solide est en mouvement par rapport à un fluide, il subit une force de frottement $$\vec{f}=-k \cdot \overrightarrow{v^{n}}$$ qui est toujours colinéaire au vecteur vitesse $$\vec{v}$$ mais de sens contraire
La valeur de ma force de frottement dépend de la vitesse v du solide et du coefficient k qui caractérise la nature du fluide, la forme, les dimensions et l’état de surface du solide
Si la vitesse est faible, on prend n = 1 et la force de frottement f devient f = k.v
Si la vitesse est grande, on prend n = 2 et la force de frottement devient $$f=k \cdot v^{2}$$

La deuxième loi de newton

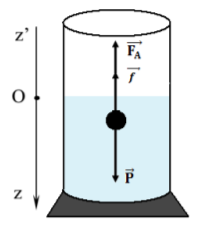
Système étudié :

la bille

Le bilan des forces :

$$\overrightarrow{F_{A}}$$ : poussée d’Archimède
$$\vec{P}$$ : Le poids de la bille
$$\vec{f}$$ : La force des frottements
Dans un repère terrestre supposé galiléen, on applique la deuxième loi de newton :

$$\vec{P}+\overrightarrow{F_{A}}+\vec{f}=m \vec{a}$$
En projetant la relation vectorielle sur l’axe vertical Oz dirigé vers le bas :
$$P_{z}-F_{A z}-f_{z}=m a_{z}$$
$$m g-\rho_{f} \cdot V_{s} \cdot g-k \cdot v^{n}=m \frac{d v}{d t}$$
En devisant sur la masse m
$$g-\frac{\rho_{f} \cdot V_{s} \cdot g}{m}-\frac{k}{m} \cdot v^{n}=\frac{d v}{d t}$$
$$g\left(1-\frac{\rho_{f} \cdot V_{s}}{m}\right)-\frac{k}{m} \cdot v^{n}=\frac{d v}{d t}$$

L’équation différentielle

L’équation différentielle de ce mouvement s’écrit sous la forme
$$A-B v^{n}=\frac{d v}{d t}$$
Avec
A : $$g\left(1-\frac{\rho_{f} \cdot V_{s}}{m}\right)$$
B : $$\frac{k}{m}$$

La vitesse limite

Regardons de plus près l’équation différentielle, on voit que si le membre de droite est nul, alors la dérivée de la vitesse par rapport au temps est nulle, donc la vitesse atteint une valeur limite qui ne varie plus

Tant que v est constante alors : $$\frac{d \mathrm{v}}{d \mathrm{t}}=0$$ et $$v=v_{l i m}$$, l’équation différentielle devient :
$$A-B v_{l i m}^{n}=0$$
Alors
$$v_{l i m}=\sqrt[n]{\frac{A}{B}}$$

L’accélération initiale $$a_{0}$$ 

A l’instant t=0, on a $$\frac{d v}{d t}=a_{0} \text { et } v=v_{0}=0$$
Alors l’équation différentielle $$A-B v^{n}=\frac{d v}{d t}$$ devient :
$$a_{0}=A=g\left(1-\frac{\rho_{f} \cdot V_{s}}{m}\right)$$

La représentation graphique

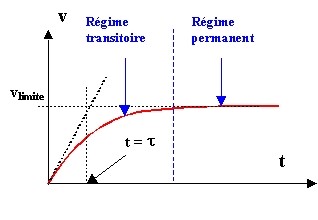
A l’instant du lâcher, la bille tombe dans le fluide avec une vitesse croissante : c’est le régime initial.
Au cours de la chute, la vitesse continue d’augmenter, mais moins rapidement : c’est le régime transitoire.
Si la chute dure suffisamment longtemps, la bille atteint une vitesse limite : c’est le régime permanent.
D’après la représentation graphique on peut déterminer $$V_{\text {lim }} \text { et } \tau$$

Le temps caractéristique du mouvement

Le temps caractéristique peut être déterminé en traçant la tangente à la courbe à t = 0 s : l’abscisse du point d’intersection de cette tangente et de l’asymptote à la courbe a pour valeur $$\tau$$ .

D'après la courbe on a : $$\left.a_{0}=\frac{d V}{d t}\right)_{0}=\frac{V_{l i m}-V_{0}}{\tau-0}$$
$$\tau=\frac{V_{l i m}}{a_{0}}$$

La méthode d’Euler

La méthode d’Euler est une méthode numérique itérative qui permet d’évaluer, à intervalles de temps réguliers, différentes valeurs approchées à partir des conditions initiales.
On peut déterminer les grandeurs cinétiques (vitesses et accélérations) par deux équations :
$$a_{i}=A-B v_{i}^{n}$$
$$v_{i+1}=v_{i}+a_{i} \cdot \Delta t$$
Avec \Delta t est le pas de calcul : $$\Delta t=t_{i+1}-t_{i}$$

Chute libre verticale d’un solide

لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

النسخة المجانية لكيزاكو:

• ملخصات الدروس غير محدودة
• فيديو مجاني في كل درس
• تمرين مصحح مجاني
• اختبار تفاعلي

إنشاء حساب مجاني