Modélisation des liaisons cinématiques
Une fois l’énergie d’entrée converti de manière convenable en énergie de sortie, Il s’agit maintenant de la faire passer par les systèmes de transmission afin d’être utilisée par la partie opérative. Cette partie du cours ne va traiter que les mécanismes (ou bien les systèmes et modes de transmission) de l’énergie mécanique à elle seule.
Transmettre
تعريف
L’énergie qui sera manipulée et traitée dans tout le reste du cours est l’énergie mécanique, de rotation ou bien de translation. Donc l’ensemble du cours portera sur les solutions technologiques mises en vigueur pour assurer une bonne transmission de l’énergie mécanique.
Mécanisme, degré de liberté
On appelle mécanisme tout dispositif assurant la fonction de transmission de l’énergie mécanique. Il s’agit donc d’un système de solides (pièces mécaniques) reliées entre elles par des liaisons mécaniques. Le jeu des pièces mécaniques assemblées et des mouvements possibles permet la manipulation directe de l’énergie reçue.
Degrés de liberté d’un point matériel
On modélise un solide (S) comme étant une infinité de points matériels $M(x, y, z)$ rassemblés dans un volume d'espace $V$ et reliés de manière rigide. Exemple : une table en bois est un solide, constitué d'une infinité de particules élémentaires qui constituent le matériau bois. Donc un point matériel dans l'espace peut se déplacer selon les trois directions de base d'un repère orthonormé $O(i, j, k)$, ces trois déplacements (qu'on appelle translations) sont les trois degrés de liberté d'un point dans l'espace. $\begin{array}{lll}D_{x} & D_{y} & D_{z}\end{array}$ Donc la donnée cinématique d'un point est entièrement déterminée par 3 coordonnées.
Degrés de liberté d’un solide
Un solide est une infinité de points matériels confinés dans un volume, il dispose donc de base de 3 degrés de libertés en translation, s’ajoutent à ceux-ci trois autres degrés de liberté (appelés rotations) qui décrivent la tendance du solide à tourner autour d’un ou plusieurs axes; un solide est doté donc de 6 degrés de liberté, trois translations et trois rotations. $\begin{array}{ccc}D_{x} & D_{y} & D_{z} \\ R_{x} & R_{y} & R_{z}\end{array}$
Liaisons
Une liaison entre deux solides est un ensemble de contacts entre les deux, qui bloquent un nombre de degrés de liberté afin de maitriser le mouvement conservé entre ces deux pièces. (exemple : Le pivot d’une porte est une liaison entre la porte et le mur). On classifie les contacts en trois types, selon la dimension des éléments de contact entre deux solides.
Classification des contacts
Contact ponctuel
Un contact entre deux solides est dit ponctuel lorsque les deux solides intersectent au niveau d’un seul point.
Contact linéique
Un contact entre deux solides est dit linéique (ou linéaire) lorsque les deux solides intersectent au niveau d’une ligne ou une courbe.
Contact surfacique
Un contact entre deux solides est dit surfacique lorsque les deux solides intersectent au niveau d’un plan ou une surface.
Liaisons élémentaires
Nous regroupons dans la partie suivante un ensemble de liaisons qui diffèrent par les degrés de liberté bloqués et libérés. L’ensemble des conditions cinématiques sera représenté comme suit : $\left\{D_{x} R_{x} D_{y} R_{y} D_{z} R_{z}\right\}$
La valeur 0 sera affecté à chaque ddl (degré de liberté) bloqué, et la valeur 1 sera affecté à un ddl libéré.
|
Nom |
Schéma 3D ex |
DDLs |
Symbole normalisé |
| Encastrement | 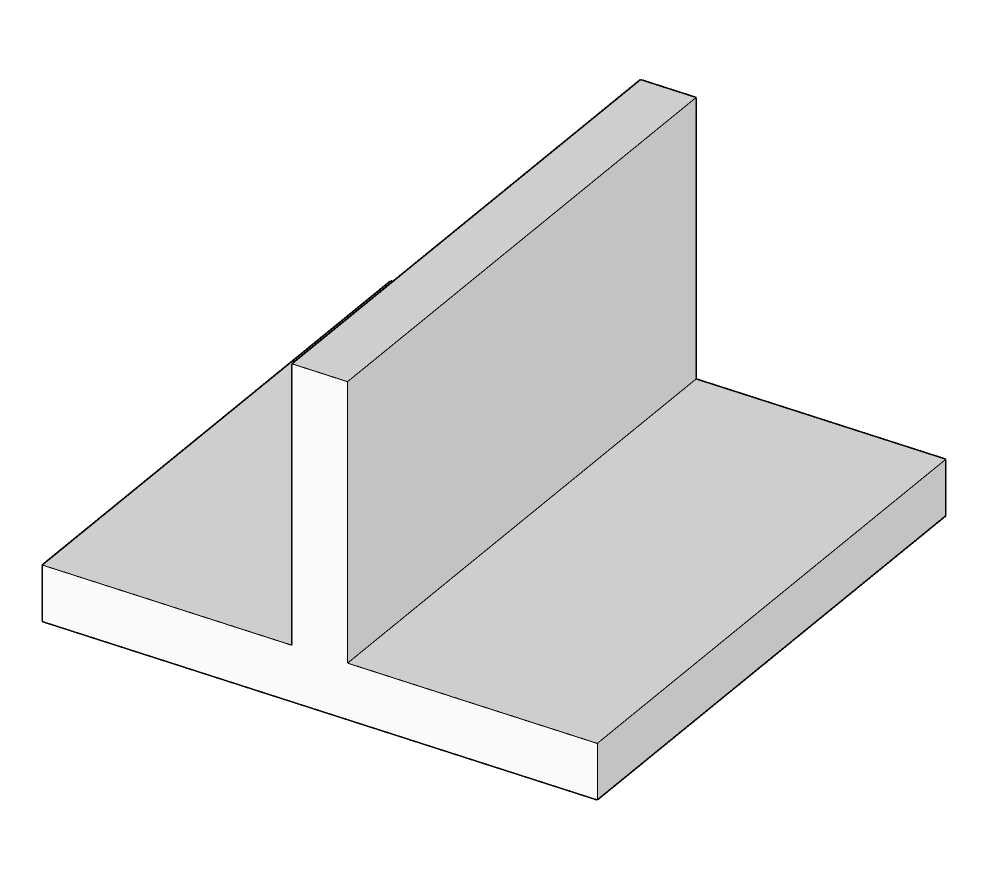 |
$$\left\{ \begin{array}{r c l} D_x = & 0 \\ D_y = & 0 \\ D_z = & 0 \end{array} \right .$$ | 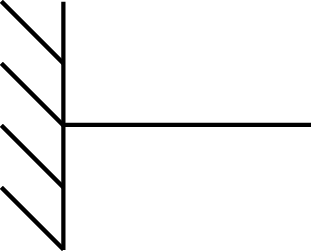 |
| Glissière | 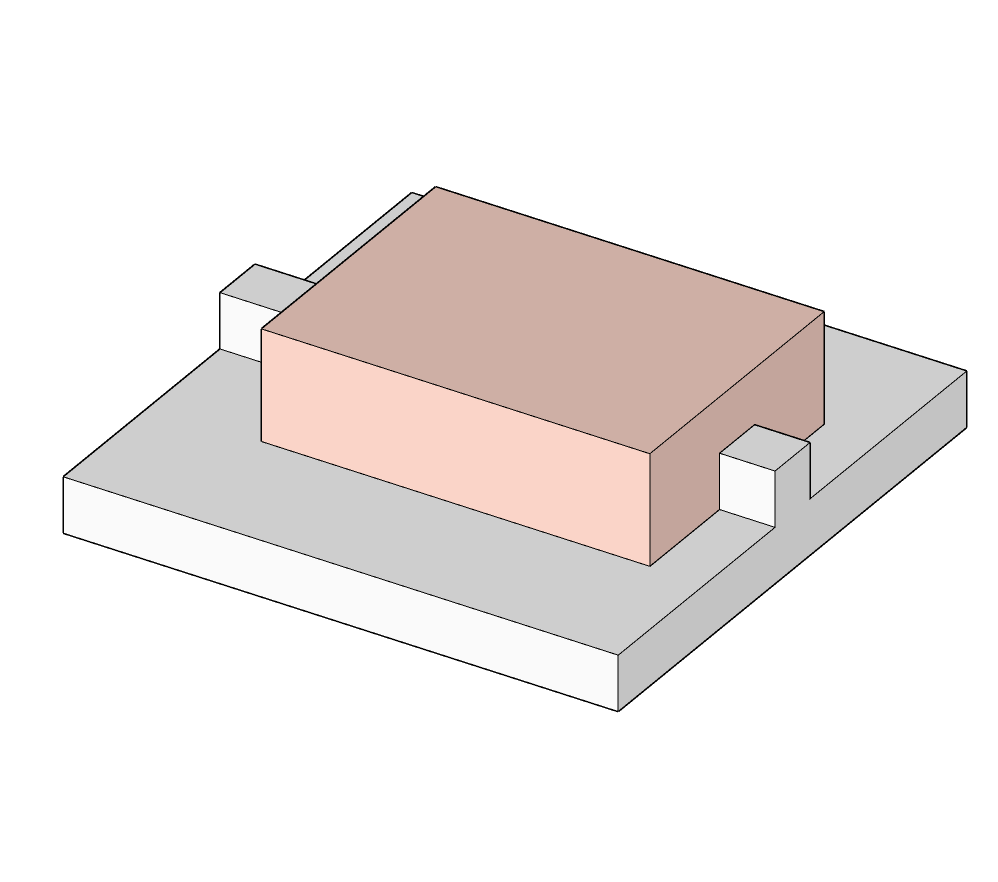 |
$$\left \{ \begin {array}{r c l} D_x = & 1 \\ D_y = & 0 \\ D_z = & 0 \end{array}\right .$$ |  |
|
Pivot |
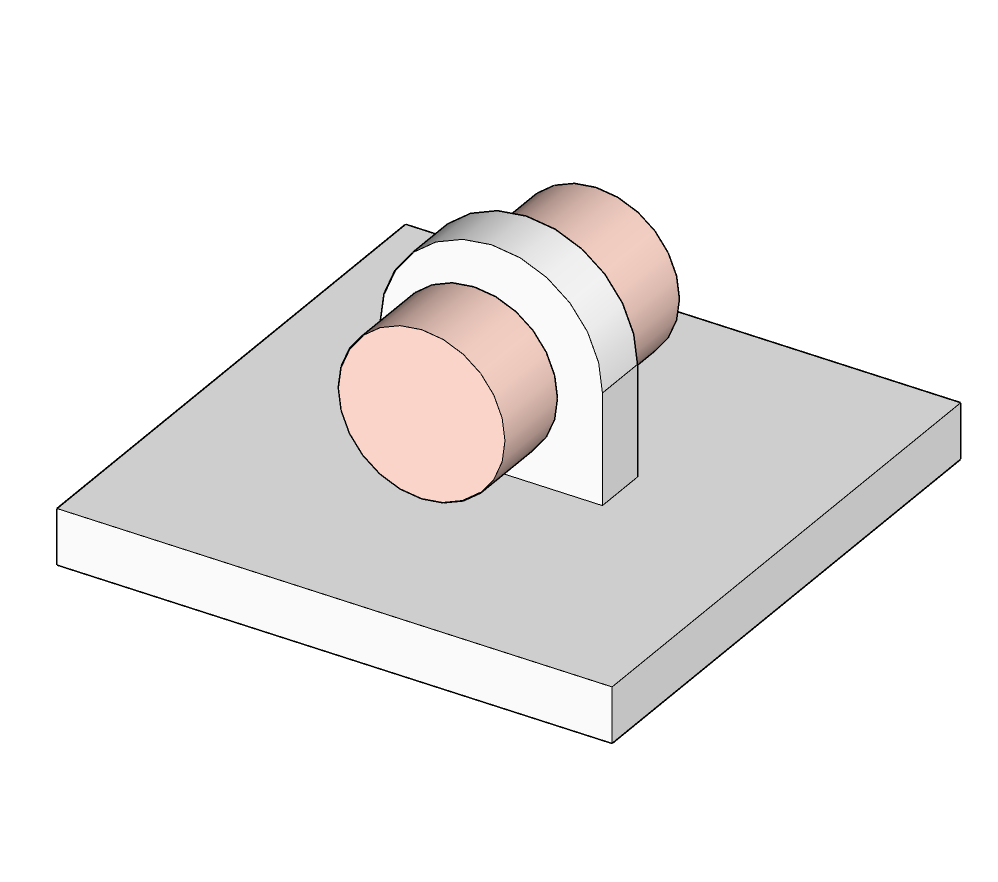 |
$$\left \{ \begin{array}{r c l} D_x = & 0 \\ D_y = & 0 \\D_z = & 0 \end {array}\right .$$ |  |
| Pivot glissant | 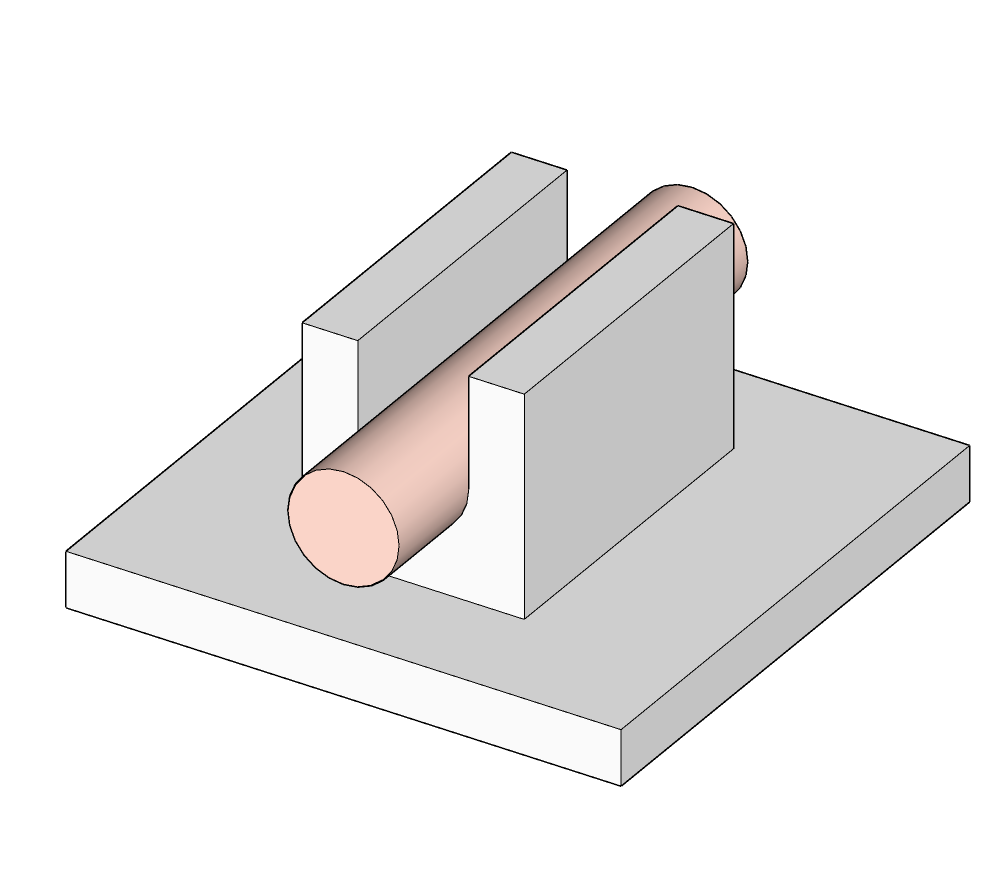 |
$$\left \{ \begin {array}{r c l} D_x = & 0 \\ D_y = & 1 \\ D_z = & 0 \end {array} \right .$$ |  |
| Rotule | 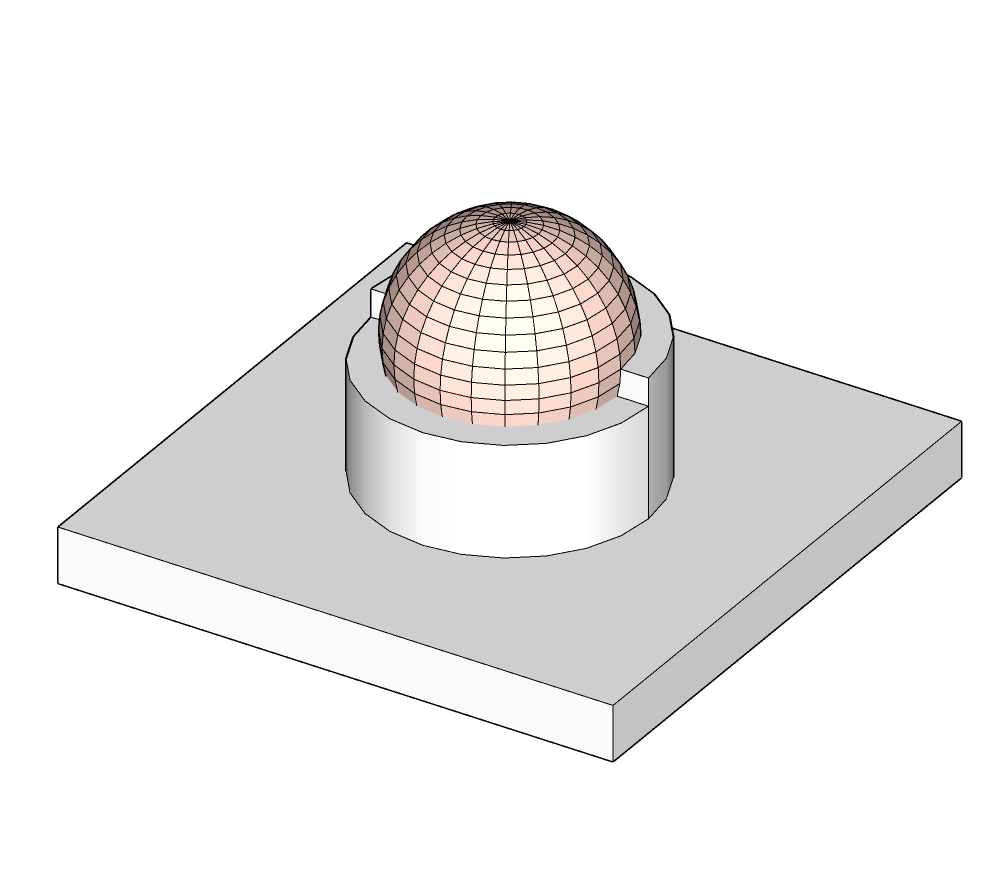 |
$$\left\{\begin {array}{r c l}D_x = & 0 \\ D_y = & 0 \\ D_z = & 0 \end{array}\right .$$ | 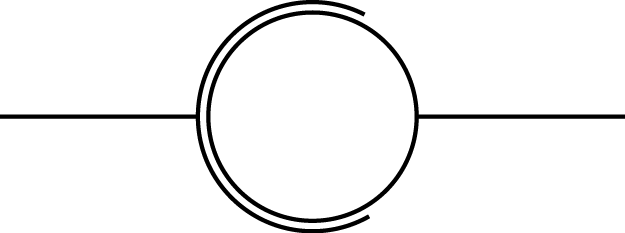 |
| Hélicoïdale* | 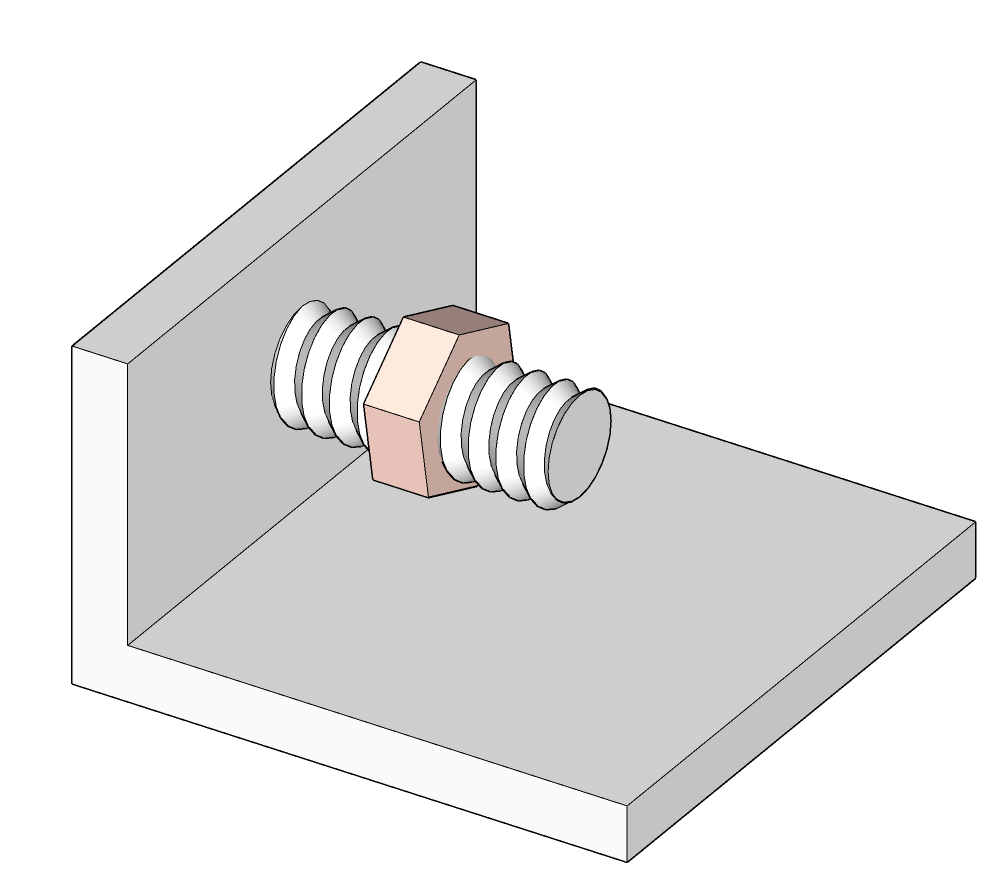 |
$$\left\{\begin {array}{r c l}D_x = & 1 \\D_y = & 0 \\D_z = & 0 \end {array}\right .$$ | 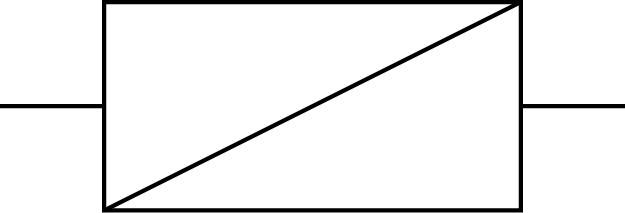 |
Pour la liaison hélicoïdale, la rotation et la translation sont couplées et se font en même temps (système vis-écrou).
Représentation cinématique d’un système
Objectif
Nous revenons à l’idée de base qu’un mécanisme est un ensemble de pièces mécaniques reliées entre elles par des liaisons dont le but est d’obtenir un mouvement précis et bien déterminé. L’objectif est donc de savoir caractériser les pièces mécaniques en mouvement relatif et de décrire ces mouvements relatifs afin de bien schématiser le comportement cinématique du mécanisme. La finalité du modèle (ou bien schéma) cinématique est d’étudier les mouvements entre-pièces et analyser le fonctionnement et l’architecture du mécanisme.
Classes d’équivalence et méthode de représentation
Dans un mécanisme, l’ensemble des pièces est généralement divisé en sous-ensembles de manière telle que pour un sous-ensemble donné, l’ensemble des pièces constitutives de celui-ci sont en liaison fixe (encastrement) entre elles. Un ensemble de pièces mécaniques en liaison fixe est appelé classe d’équivalence. Un système de transmission peut avoir autant de classes d’équivalence que possible, donc un exercice récurrent est de déterminer les classes d’équivalence d’un système, car les liaisons sont toujours assurées entre les classes d’équivalence.
A partir de là, la suite devient méthodique :
- Une fois les classes d’équivalence déterminées et recensées, on identifie les liaisons existantes entre les classes.
- Ensuite on établit un graphe des liaisons où on représente les C.E (classes d’équivalence) avec des bulles reliés par des traits représentant les liaisons.
- A partir du graphe des liaisons, le schéma cinématique est établi sans problème.
|
Nom |
DDLs |
symbole |
| Encastrement |
0T-0R |
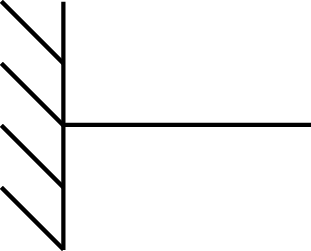 |
| Pivot |
0T-1R |
 |
| Pivot glissant |
1T-1R |
 |
| Glissière |
1T-0R |
 |
| Hélicoïdale |
1T-R |
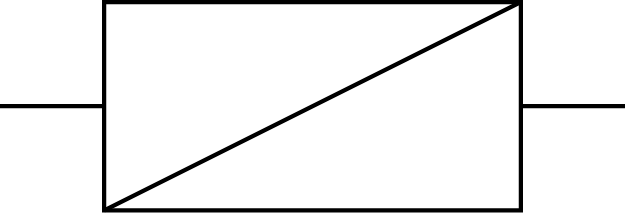 |
| Sphérique à doigt |
0T-2R |
 |
| Rotule |
0T-3R |
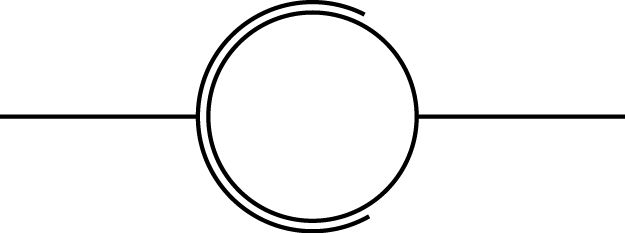 |
| Appui plan |
2T-1R |
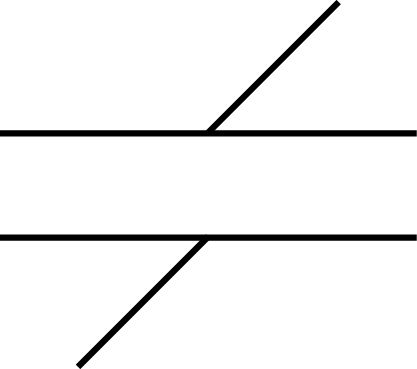 |
| Linéaire annulaire |
1T-3R |
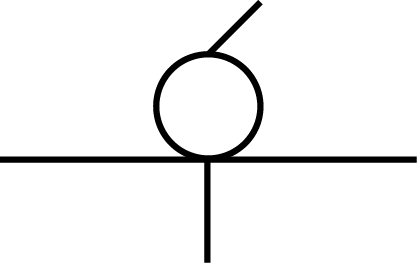 |
| Linéaire rectiligne |
2T-2R |
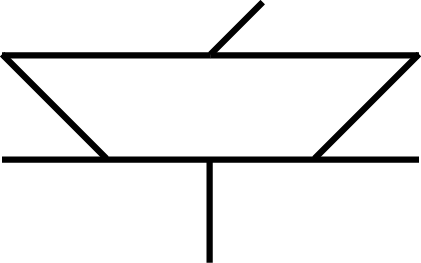 |
| Ponctuelle |
2T-3R |
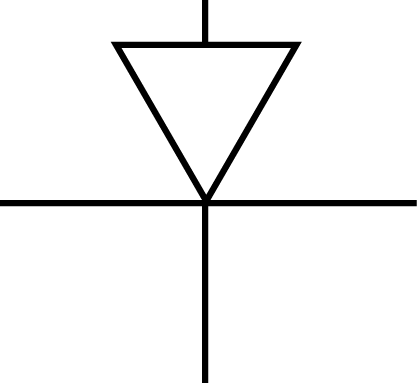 |
ما يجب معرفته
Transmettre, c’est manipuler une énergie utilisable directement de manière à ce que la partie opérative puisse satisfaire les consignes données par la partie commande .
On appelle mécanisme tout dispositif assurant la fonction de transmission de l’énergie mécanique.
Connaitre les 6 degrés de liberté, les types de contacts et les liaisons élémentaires ainsi que leurs degrés de liberté permis.
N.B. : Pour la liaison hélicoïdale, la rotation et la translation sont couplées et se font en même temps (système vis-écrou).
Les classes d’équivalence et la méthode pour dresser le schéma cinématique et le graphe des liaisons.
La liaison encastrement
L’objectif de ce chapitre est de traîter l’opération de concrétisation d’une liaison encastrement en explicitant toutes les considérations mécaniques à prendre en compte afin de bien modéliser et d’assurer la liaison comme il se doit.
Analyse fonctionnelle de la liaison encastrement
A.F externe
Pieuvre

Diagramme pieuvre d’un encastrement généralisé.
SADT

Diagramme SADT A-0 d’un encastrement généralisé.
Diagramme FAST
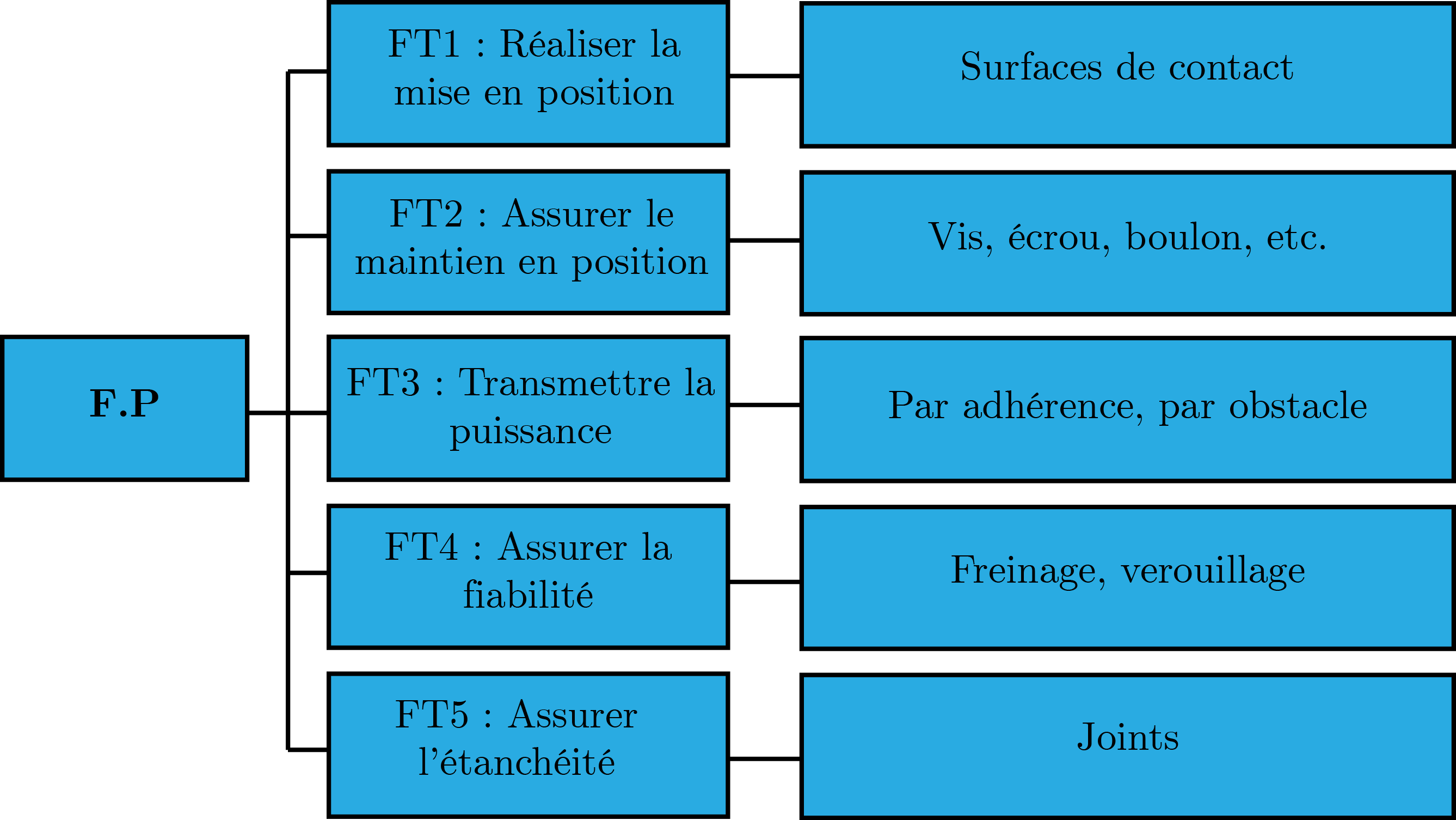
Diagramme FAST d’un encastrement généralisé.
Caractérisation et classification des encastrements
Mise en position, maintien en position : MIP/MAP
La mise en position (MIP) est une fonction technique de l’encastrement qui est réalisée au moyen des zones de contact et surfaces de contact qui participent au blocage des degrés de liberté; un MIP en encastrement bloque 6 degrés de liberté dans l’espace et 3 degrés de liberté en plan.
Le maintient en position (MIP) est une fonction technique qui est réalisée au moyen des pièces mécaniques qui assurent la/les fixation(s) entre les deux pièces à lier.
Caractérisation des liaisons
Les liaisons sont caractérisés par les modes de réalisation ainsi que leurs propriétés intrinsèques :
- Liaison complète : Élimine tout mouvement relatif entre les deux pièces liées.
- Liaison partielle : Permet un mouvement relatif entre les deux pièces liées.
- Liaison rigide : Comporte un élément de liaison indéformable (par rapport aux pièces reliées), risque de déformation différée minime.
- Liaison élastique : Comporte un élément déformable qui revient à sa situation initiale une fois que la liaison n’est plus sollicitée.
- Liaison par adhérence : Le blocaqe d’un DDL se fait par adhérence (colle, soudure etc).
- Liaison par obstacle : Le blocage d’un DDL se fait par un obstacle extérieur qui empêche le mouvement dans la direction souhaitée.
- Liaison démontable : La liaison est assemblable et désassemblable sans endommagement partiel ou complet.
- Liaison permanente : Lorsqu’une tentative de désassemblage comporte un risque de perte de fonction.
- Liaison directe : Lorsque la liaison est assurée par les pièces elles-mêmes.
- Liaison indirecte : Lorsque la liaison entre deux pièces se fait à travers une troisième pièce.
Classification des encastrements
Les encastrements sont donc des liaisons complètes (et par conséquent rigides dans le cadre du programme), nous les classifierons donc en encastrements démontables et permanents, les encastrements démontables seront à leur tour classifiés en encastrements par adhérence et par obstacle.
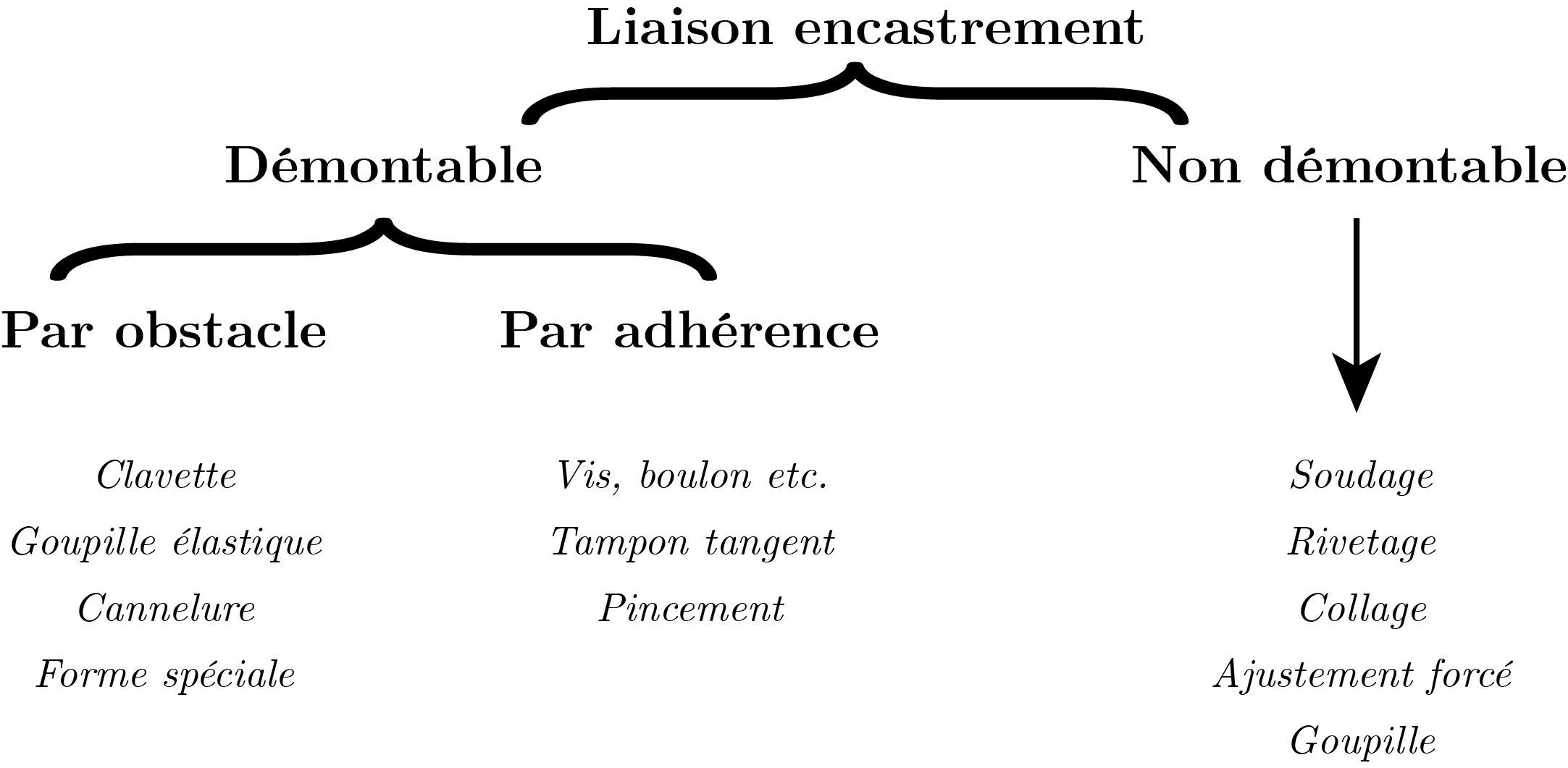
Classification d’un encastrement.
Méthodes de réalisation des encastrements
Encastrements démontables par adhérence
Filetage
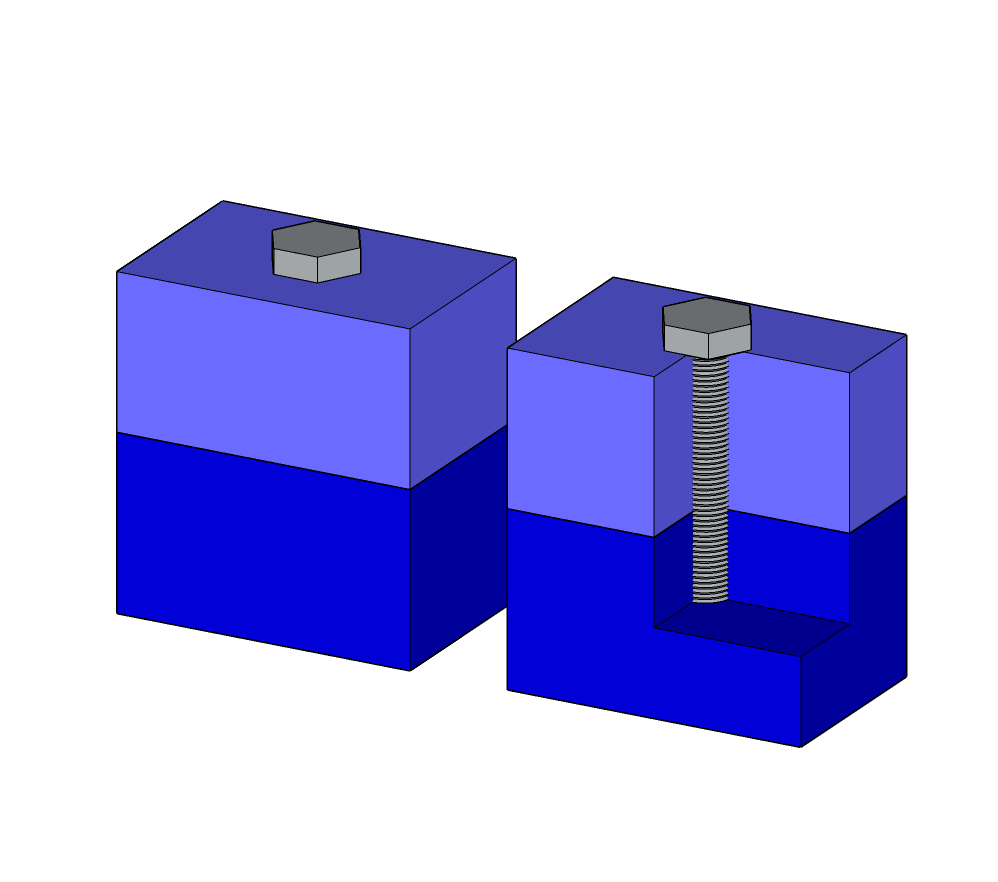
Encastrement par filetage, la MIP se fait à travers la surface place de contact filetage-taraudage.
Pincement
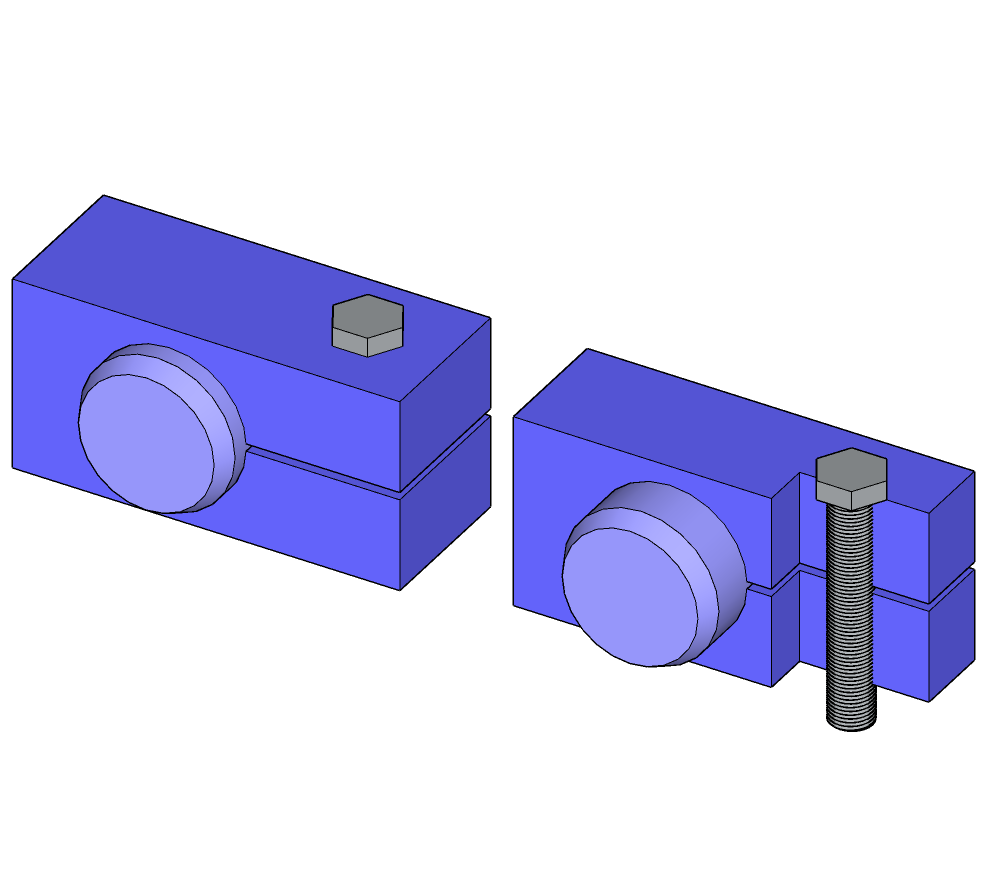
Encastrement par pincement, la MIP se fait à travers la surface cylindrique de contact, le boulon d’assemblage assure le MAP en serrant la partie extérieure.
Tampon tangent
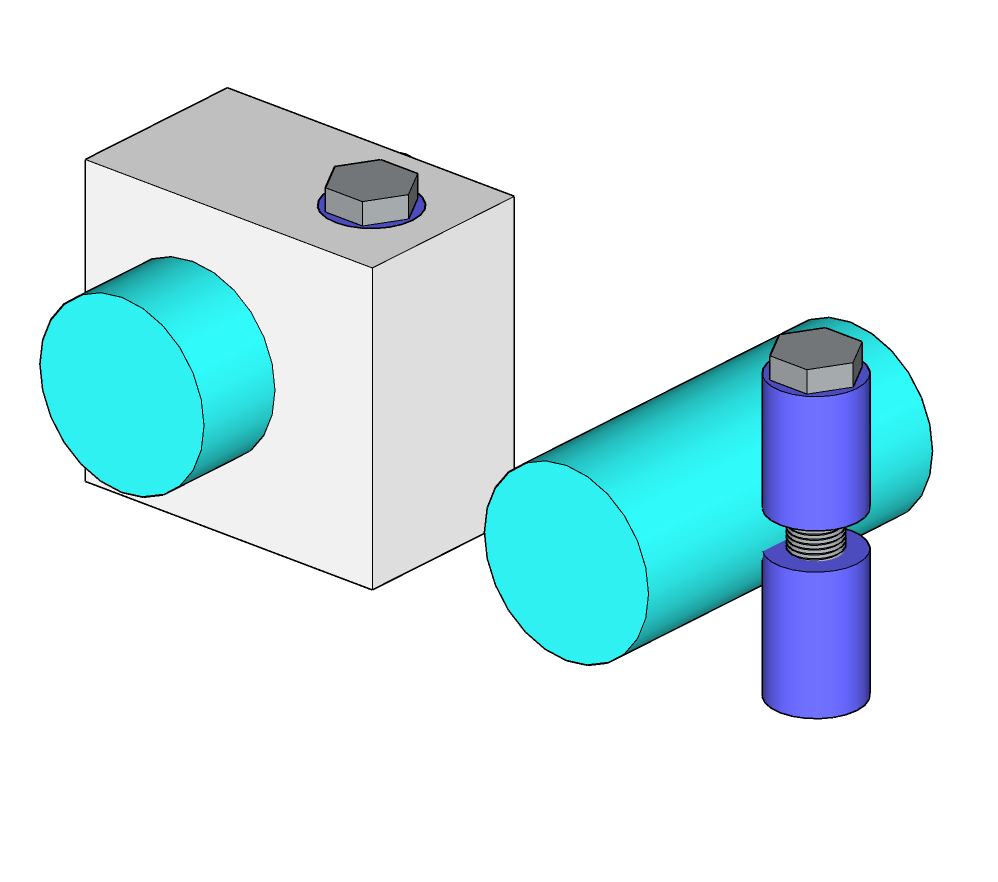
Encastrement par tampon tangent, la MIP se fait à travers la surface cylindrique de contact, le boulon d’assemblage assure le MAP en serrant la partie extérieure.
Emmanchement conique
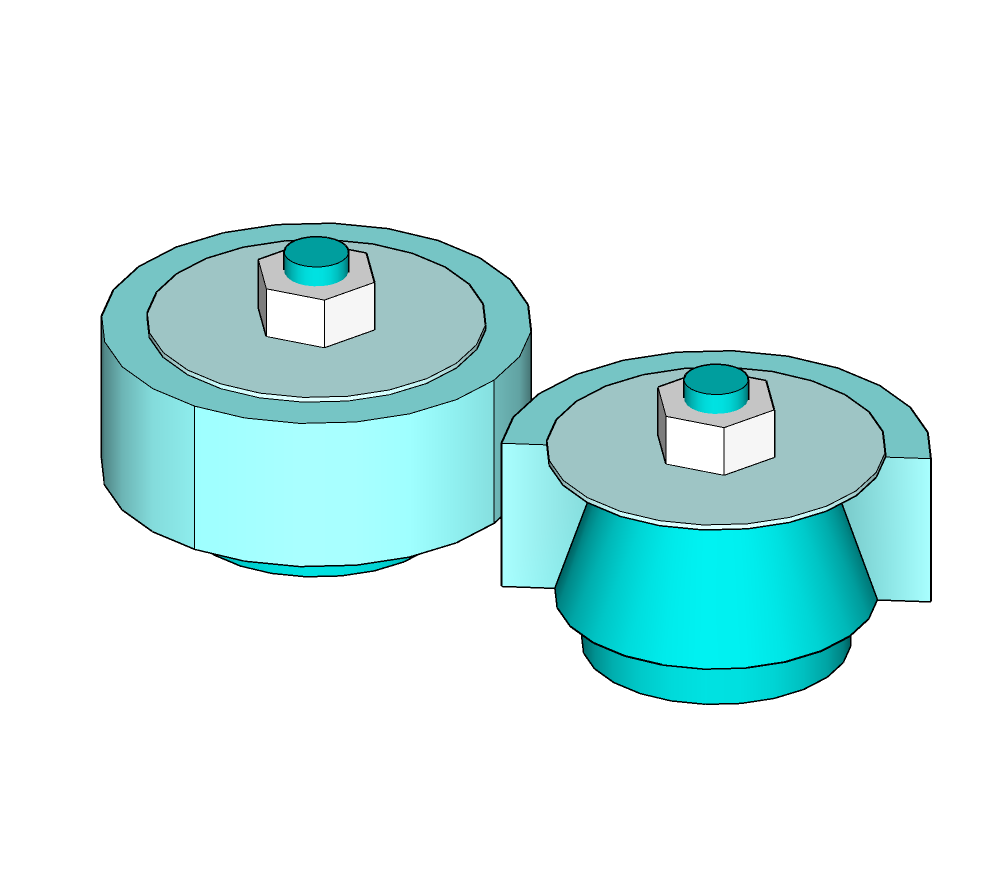
Encastrement par emmanchement conique, la MIP se fait à travers la surface conique de contact, le MAP est assuré par un éventuel écrou+rondelle.
Encastrements démontables par obstacle
Goupille
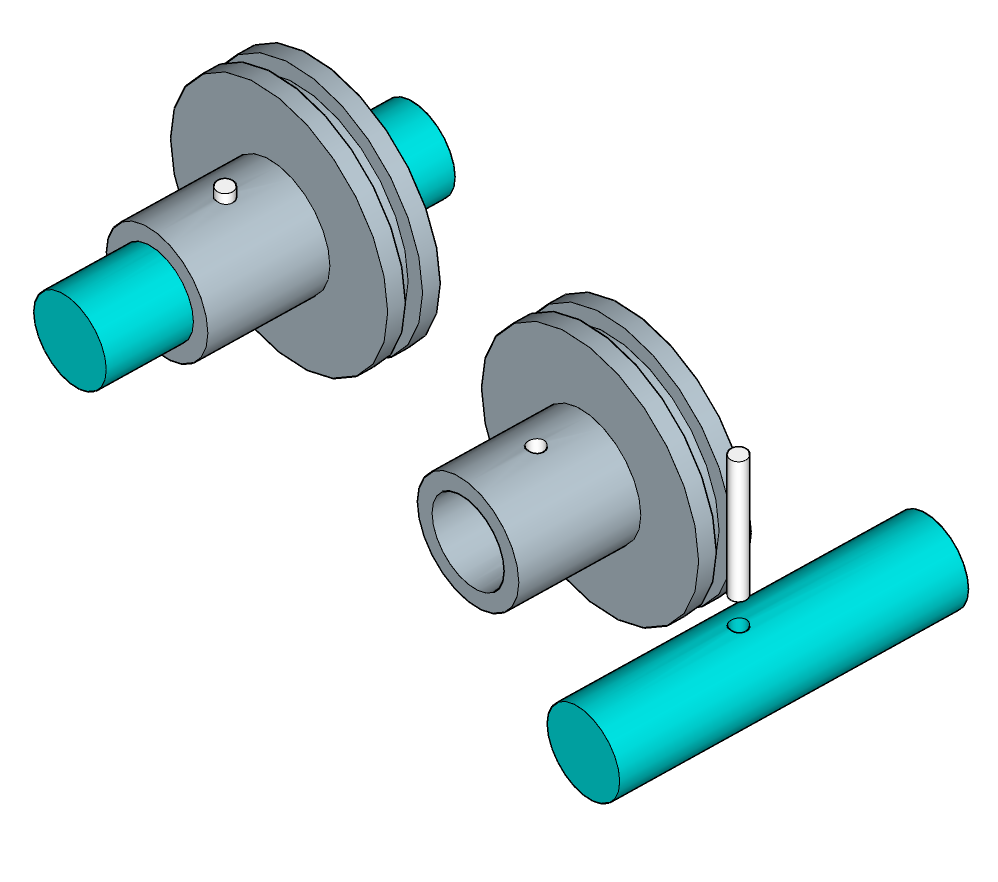
Encastrement par goupille, la MIP se fait à travers la surface cylindrique de contact entre la goupille et les éléments assemblés, le MAP est assuré par la goupille elle-même.
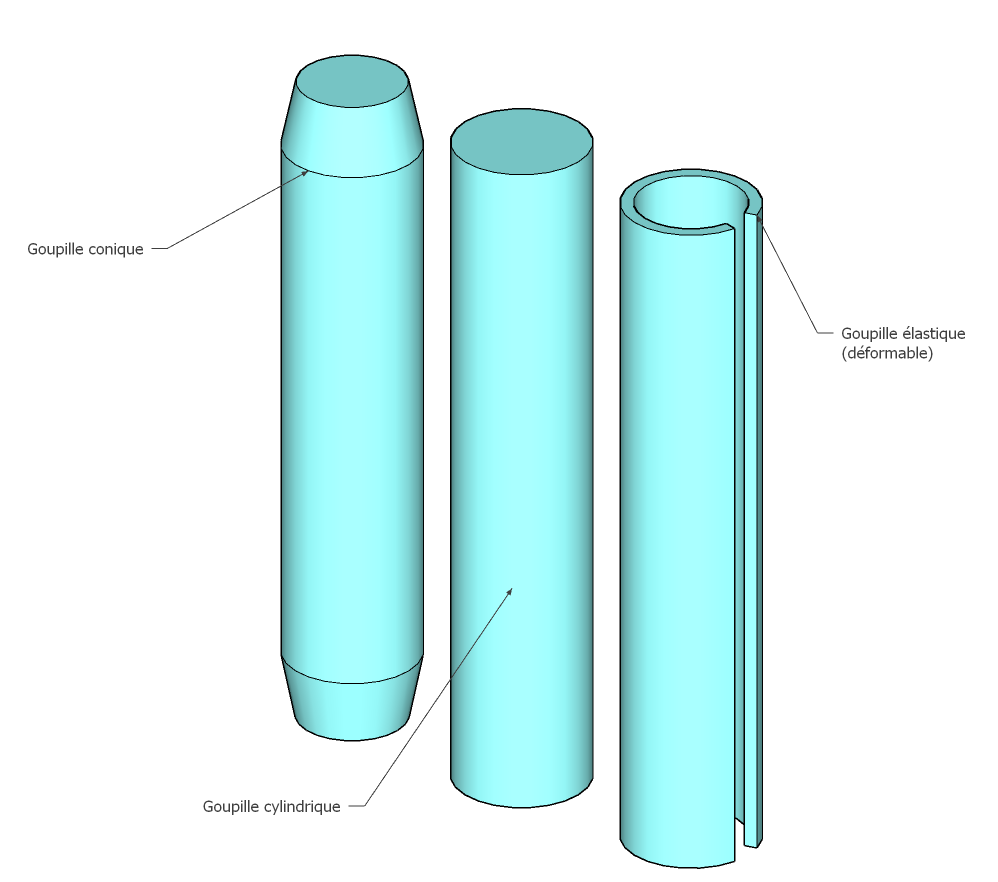
Typologies des goupilles.
Clavette
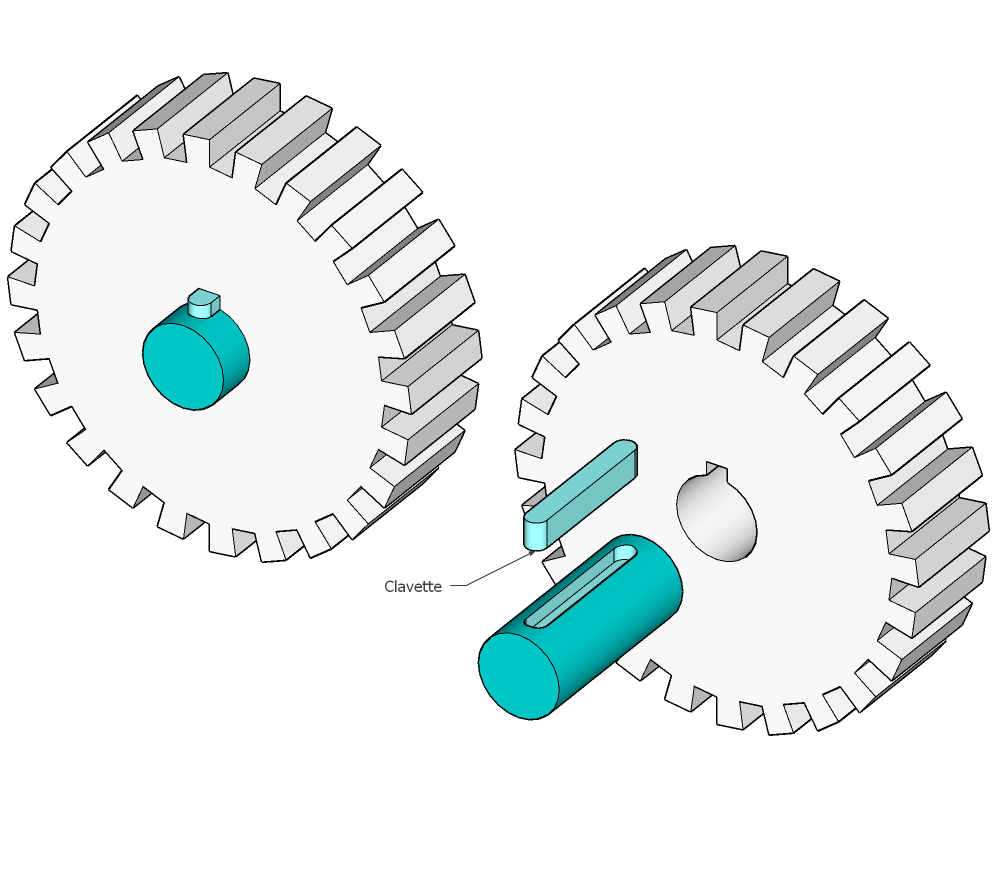
Encastrement par clavette, la MIP se fait à travers la surface cylindrique, la surface place de contact entre la clavette et les éléments assemblés.
Cannelure
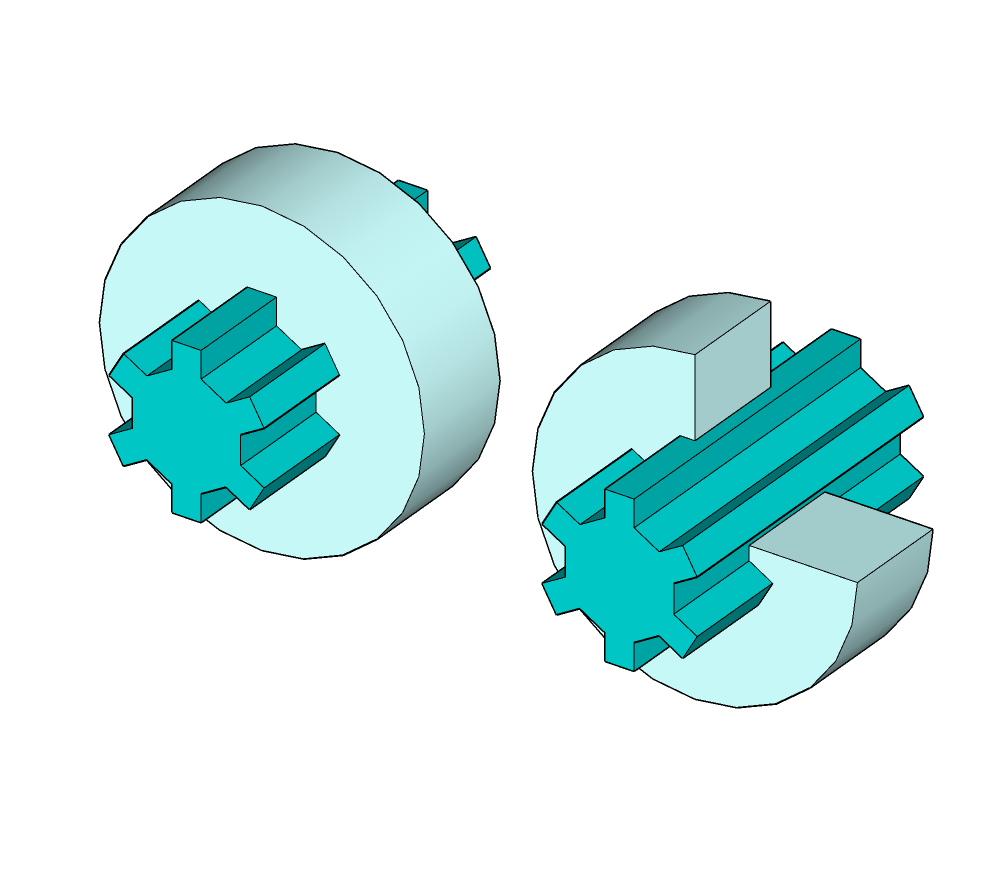
Encastrement par cannelure, la MIP se fait à travers la surface de la cannelure.
Forme spéciale
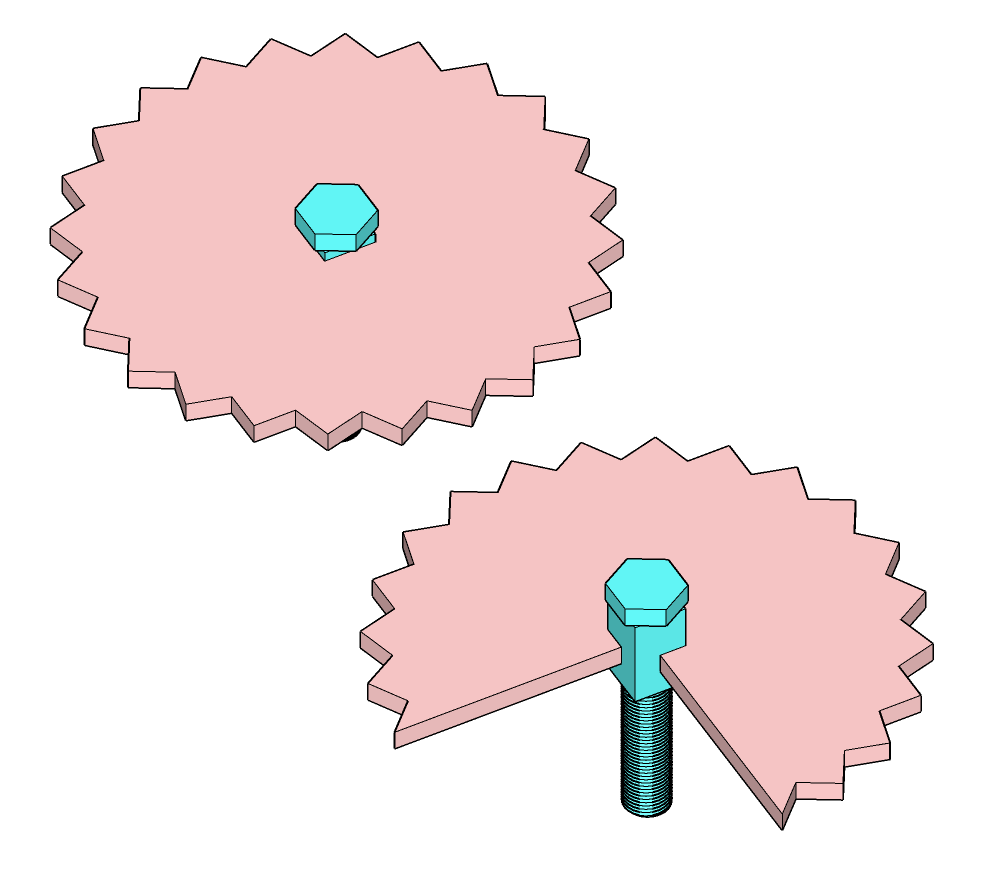
Encastrement par forme spéciale, la MIP se fait à travers la surface de la forme, l’encastrement par cannelure est un cas spécial de l’encastrement par forme spéciale.
Encastrements permanents
Emmanchement forcé
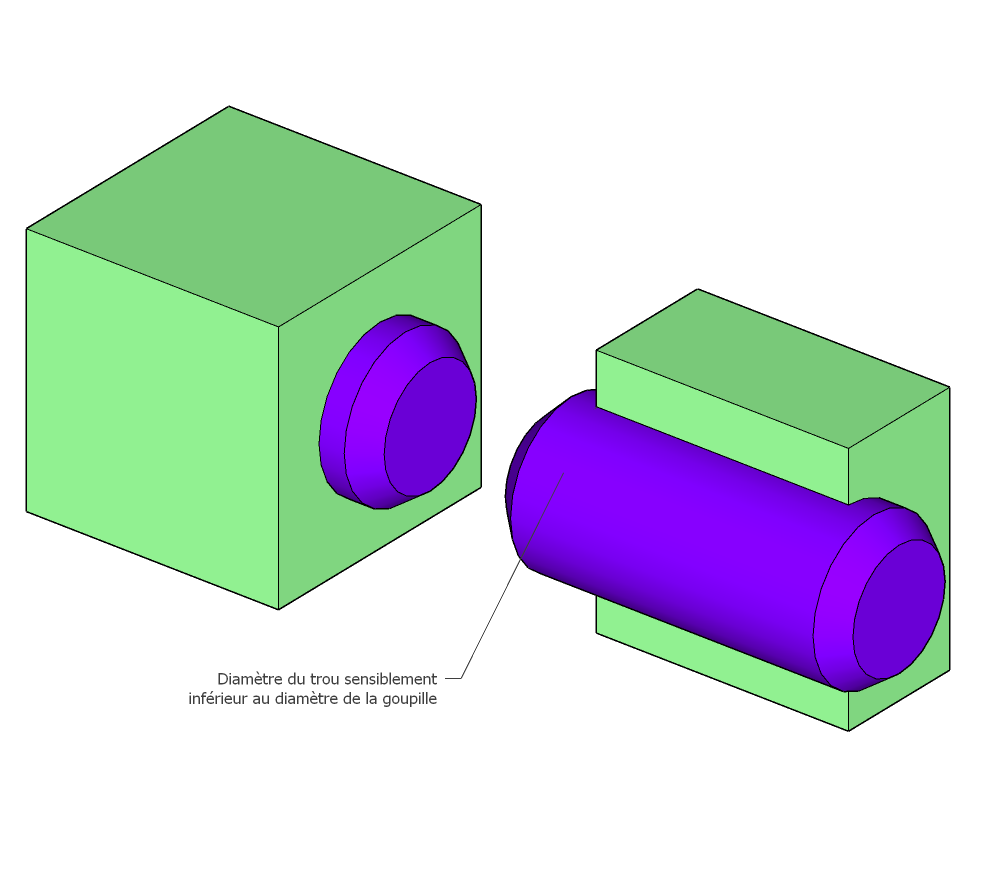
Encastrement par emmanchement forcé; le MAP est assurée par le diamètre de l’arbre qui est sensiblement supérieur au diamètre du trou, le forçage de l’arbre à l’intérieur créée l’encastrement.
Rivetage
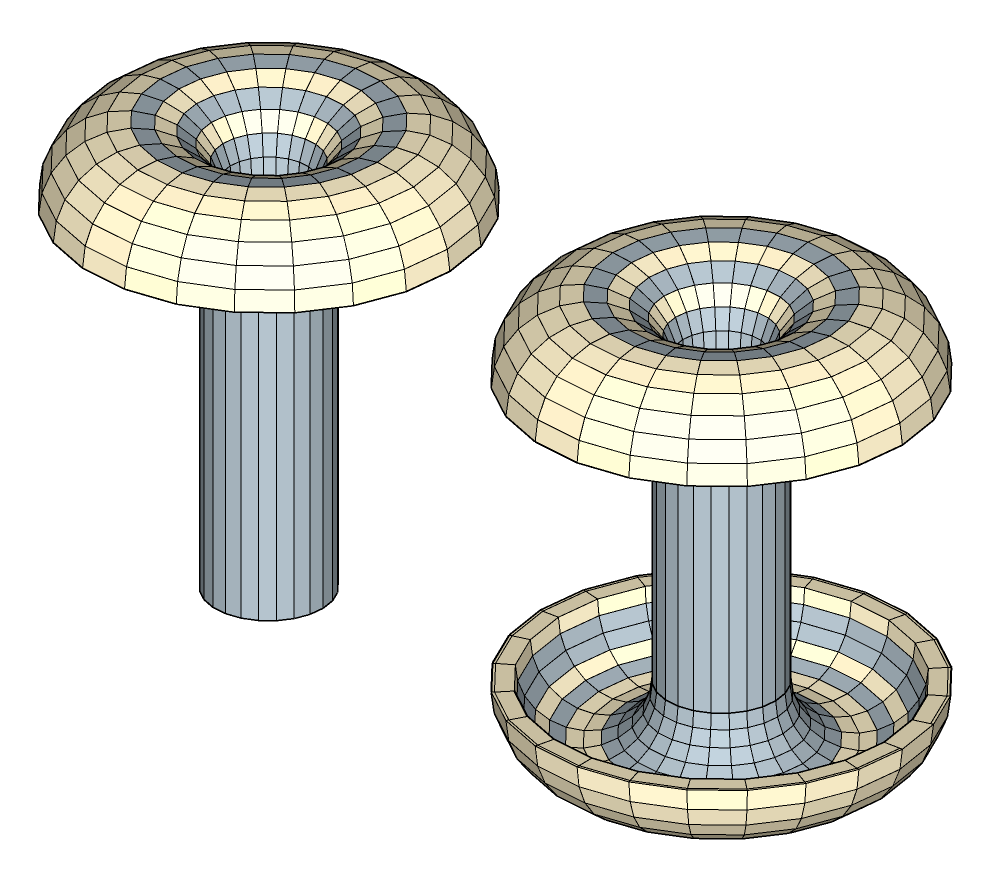
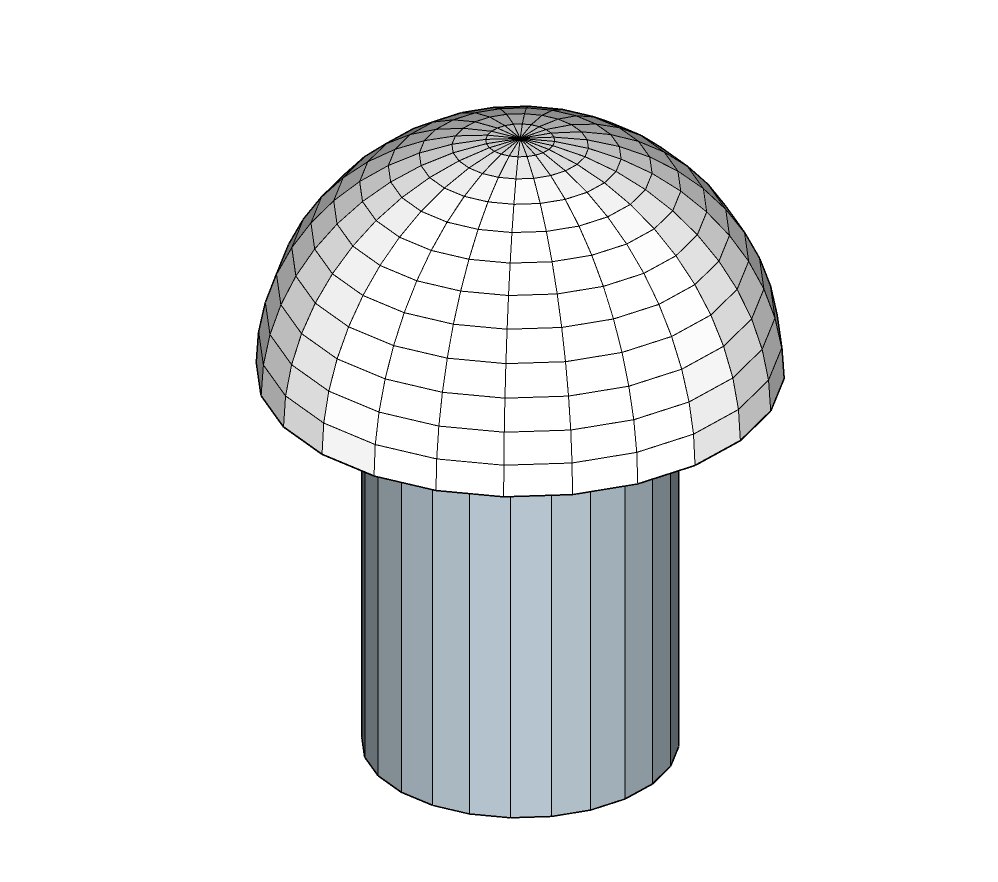
Soudage

Encastrement par soudage; le soudage à l’arc est une opération qui consiste à faire fondre une tige métallique à l’aide d’un arc électrique au niveau du point de contact entre la tige métallique et les deux pièces à souder.
Fiabilité des encastrements
Contre-écrou
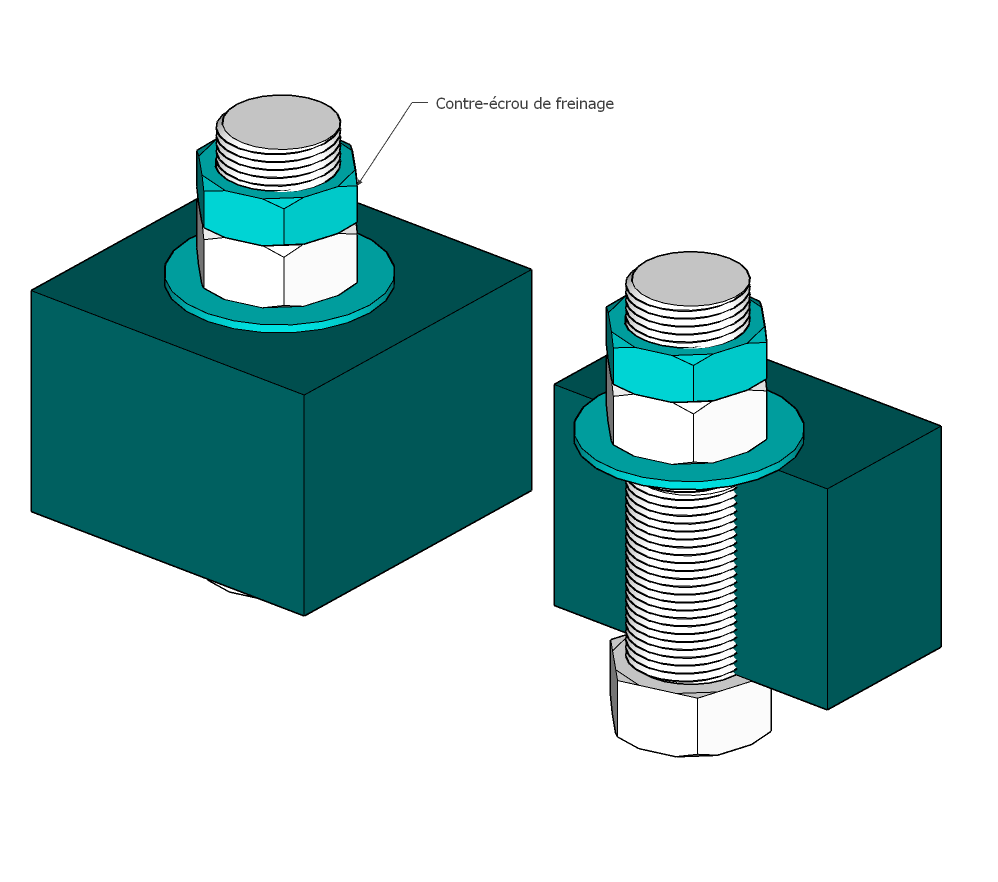
Maintien par contre-écrou : le deuxième écrou bloque l’échappement de l’écrou de MAP en cas de vibrations.
Plaquettea arrêtoir
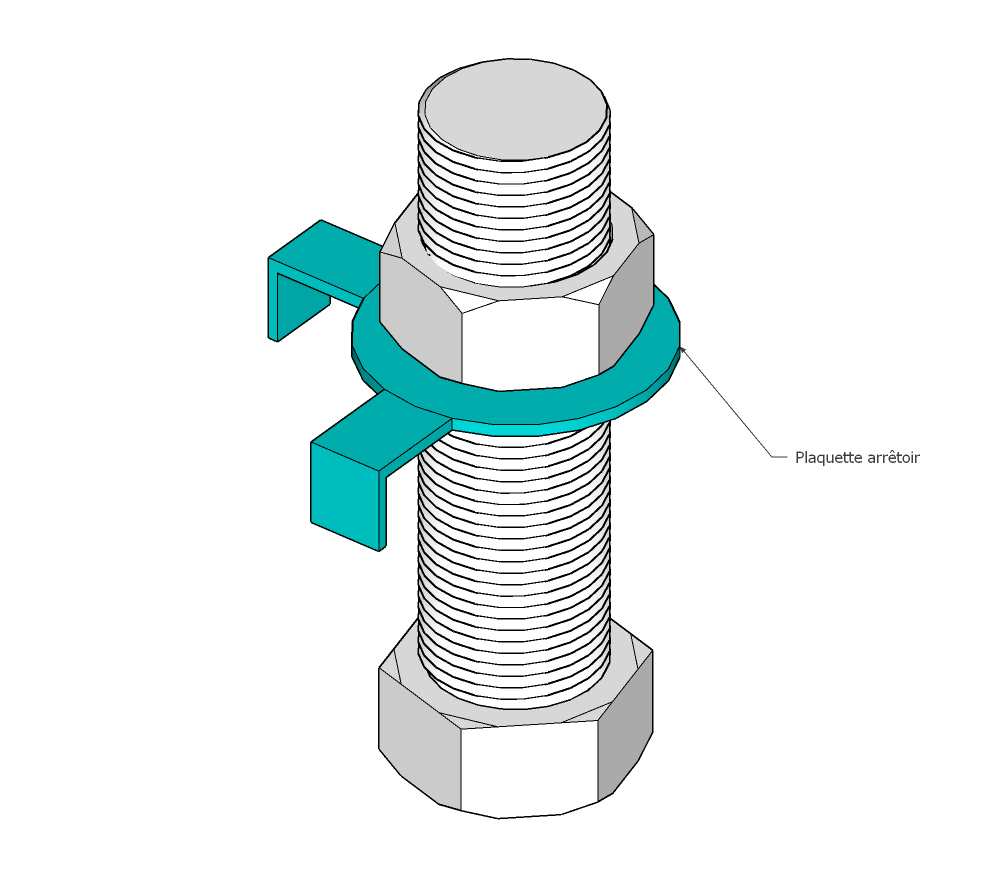
Maintien par plaquette-arrêtoir : la plaquette s’encastre avec les arêtes de la pièce à maintenir pour empêcher l’encastrement de se détacher.
Ecrou HK et goupille V

Maintien par écrou HK : L’écrou HK est un écrou taillé pour voir recevoir une goupille au niveau des encoches; la goupille s’incruste de suite avec le boulon associé.
Écrou à encoches

L’écrou à encoches est dôté de 4 encoches qui adhérent à une éventuelle languette pour assurer un freinage adéquat.
ما يجب معرفته
Un encastrement est une liaison cinématique entre deux pièces mécaniques qui bloque tous les degrés de liberté relatifs entre eux. Connaitre les différents types d’encastrement, démontables et non-démontables ainsi que la M.I.P et la M.A.P de chacune.
Les liaisons pivot et glissière
Pour continuer cette fiche de cours, Inscris-toi gratuitement sur Kezakoo

- Fiches de cours illimitées
- Une vidéo gratuite par leçon
- 2 exercices gratuits par leçon
- Un test gratuit par leçon