L’étude quantitative de la variation (la biométrie)

Introduction à l’étude de la biométrie

Si la génétique Mendélienne (classique) s’intéresse à l’étude de la transmission de caractères héréditaire de deux parents originaux à leur descendance et ce via des croisements orientés, la génétique des populations, par contre, se base sur des croisements aléatoires qui se font au niveau d’un groupe d’individus appartenant à la même espèce et occupant la même aire géographique et le mem intervalle temporel : c’est la population (dont l’étude est reportée au deuxième chapitre de cette unité). Vue cette anarchie et le nombre élevé des croisements possibles pour produire la même génération il sera difficile d’appliquer la même génétique mendélienne pour déterminer les fréquences génotypiques, phénotypiques et alléliques au sein de la population et aussi de pouvoir déceler les variations possibles qui peuvent affecter ces fréquences.

Les variations affectant les fréquences au niveau d’une population peuvent être mesurable et prévisibles alliant la génétique des populations aux sciences statistiques : c’est la biométrie, une discipline génétique permettant de :

• Mesurer la variation génétique au cours des générations
• Comprendre le mécanisme de la transmission de cette variation de génération en génération
• Comprendre et prévoir le développement des variations génétiques aux cours des générations.

Notion de variation

  L’objectif de la mesure de la transmission des caractères héréditaires chez les populations est de déterminer si la population est homogène ou non et de détecter l’apparition de quelques caractères ou phénotypes non souhaités pour l’amélioration des lignées surtout dans le domaine agricole ou l’amélioration de la production de quelques cultures en pratiquant la « sélection artificielle).

Méthodes utilisées pour l’étude quantitative de la variation

     Puisqu’il s'agit de statistiques, les caractères étudiés dans cette discipline seront toujours mesurables : le poids, la taille, nombre des graines dans le fruit … et on procède comme suit :

• Collecte des données statistiques concernant le caractère étudié
• Organisation des données suivant un ordre déterminé (progressif, régressif) afin d’obtenir une série de mesures
• Transformer les données numériques en graphiques
• Analyse et interprétation des diagrammes en appliquant quelques constantes et règles mathématiques.

I- La variation continue et la variation discontinue

A- La variation discontinue

              On parle de discontinuité dans la variation étudiée lorsque les valeurs de la variable étudié se présentent sous forme de nombres entiers.

Exemple : Etude du nombre des nouveaux nés issus de chaque grossesse (chez les femelles) chez un groupe d’individus de souris (population)

1- Collecte et organisation des données

Les données à collecter :

a- la variable : nombre de nouveau-nés Xi

b- l’effectif : nombre des femelles fi (fréquence)

Les données sont ensuite organisées et présentées sous forme de tableau

Exemple

2- Représsentation graphique de la variation discontinue

Les mesures concernant ce type de variation sont représentées sous formes de:

• Diagramme en bâtons
• Courbe
• Polygone de fréquences

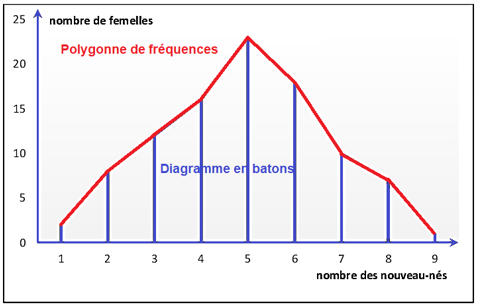
3- Analyse et interprétation

    Si le polygone de fréquences est unimodal (un seul pic) : la population est homogène et donc PROBABLEMENT formée d’une seule lignée pure. Sinon elle est hétérogène (comprenant plus d’une seule race pure)

N.B : une population homogène n’est pas obligatoirement constituée d’une seule race pure, et ainsi on aura besoin d’autres étapes pour le confirmer (les paramètres de position et de dispersion étudiés vers la fin de ce chapitre).

B- La variation continue

Dans ce deuxième cas de variation, les valeurs numériques de la variable ne se présentent pas en nombres entiers mais en intervalle de valeurs qu’on appelle « classes »

Exemple:

On mesure chez une population d’insecte la longueur des pinces chez les mâles, les résultats des mesures sont groupés et organisés en intervalles de tailles. Tous les intervalles doivent garder la même valeur de variation de taille.

1- Collecte et organisation des mesures

Les valeurs de la variables (intervalles ou classes) et leurs fréquences respectives sont organisées en ordre croissant ou décroissant dans un tableau.

Exemple:

2- Représentation graphique de la variation continue

• Histogramme de fréquences
• Polygone de fréquences
• Courbe de fréquences

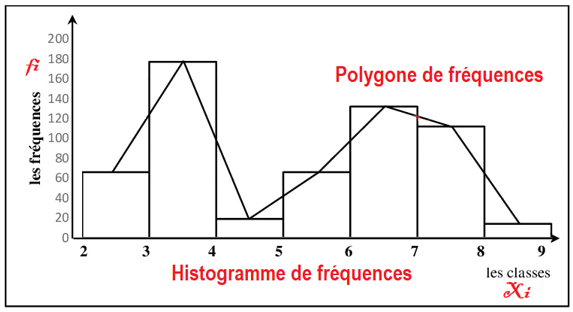
3- Analyse et interprétation

• Si le polygone (ou courbe) de fréquences est unimodal la population est homogène concernant le caractère étudié et elle est probablement constituée d’une seule race
• Si le polygone est polymodal la population est hétérogène et est donc constituée de plusieurs races

Les diagrammes représentatifs de la variation des fréquences n’est pas suffisant pour démontrer la présence d’une seule race dans la population étudiée lorsque le polygone de fréquences est unimodal, mais il permet juste de nous rapprocher de cette déduction « la population est PROBABLEMENT formée d’une seule race pure » et ainsi on fait appel à d’autres paramètres pour nous en assurer.

Les résultats (concernant l'homogénéité et la pureté de la population) obtenus à partir de la représentation graphique des fréquences ne sont pas toujours fiables, du fait qu'un polygone, ou courbe, de fréquence unimodale ne confirme qu'une possible pureté de la race constituant la population étudiée et surtout l'échantillon ( de la population) choisi et ainsi on sera appelé à tester la validité des précédents résultats par de nouveaux paramètres statistiques pour confirmer si:

• L'échantillon choisi est effectivement représentatif de toute la population
• La population est effectivement homogène
• La population comporte une seule race pure

Les paramètres caractéristiques de la distribution des fréquences sont de deux types:

III- Paramètres caractéristiques de la distribution des fréquences

لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

النسخة المجانية لكيزاكو:

• ملخصات الدروس غير محدودة
• فيديو مجاني في كل درس
• تمرين مصحح مجاني
• اختبار تفاعلي

إنشاء حساب مجاني