Limites et Continuité 2BAC SM

Fiche de cours

Continuité d'une fonction en un point

تعريف

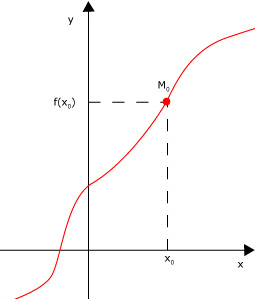
Soit $$f$$ une fonction numérique définie sur un intervalle ouvert $$I$$ et $$x_0$$ un élément de l'intervalle $I$.

On dit que la fonction $$f$$ est continue au point $$x_0$$ si:

$$\lim\limits_{x \to x_0} f(x) =f(x_0)$$

En d'autres termes:

$$(\forall \epsilon >0)(\exists \alpha >0) ~~ |x-x_0|<\alpha \Rightarrow ~~ |f(x)-f(x_0)|<\epsilon$$

مثال

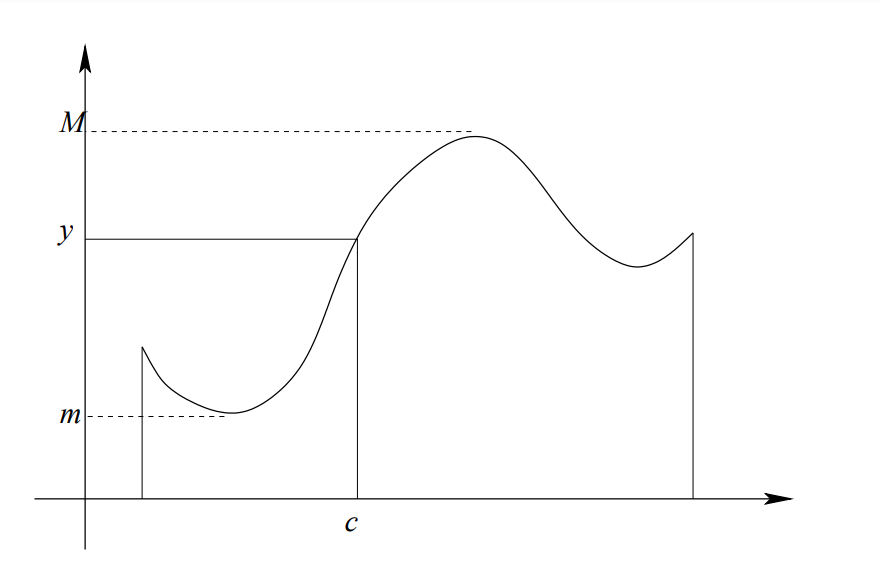
La fonction $$f$$ représentée ci-dessous est continue en $$x_0$$. La fonction $$g$$ est discontinue en $$x_0$$. Autrement dit, on voit graphiquement qu'une fonction est continue en un point $$x_0$$ si la courbe passe par le point $$M_0$$ $$(x_0 ; f(x_0))$$ sans coupure. Sinon, la fonction est discontinue en ce point.

مثال

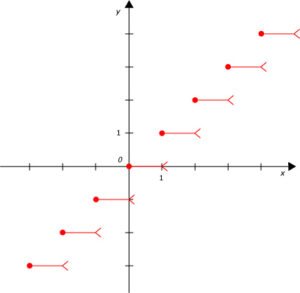
La fonction partie entière de $$x$$, notée $$E$$, est discontinue en tout point entier. $$E(x)$$ est le plus grand entier relatif inférieur ou égal à $$x. \\[0.2cm] $$ Par exemple, $$~E(\pi) = 3~~$$ ; $$~~E(-\pi) = -4~~$$ ; $$~~E(\sqrt{2}) = 1 \\[0.2cm]$$ $$E(5) = 5~~$$ et $$~~E(-8) = -8. \\[0.2cm]$$ Voici la représentation graphique de cette fonction :

Représentation graphique de la fonction Partie entière E(x)

Continuité à gauche, continuité à droite

تعريف

Soit $$f$$ une fonction définie sur l'intervalle $$[x_0 ; x_0+r[$$ où $$r>0$$

On dit que la fonction $$f$$ est continue à droite en $$x_0$$ si:

$$\lim\limits_{x \to x_0^+} f(x)=f(x_0)$$

Soit $$f$$ une fonction définie sur l'intervalle $$[x_0-r ; x_0[$$ où $$r>0$$

On dit que la fonction $$f$$ est continue à gauche en $$x_0$$ si:

$$\lim\limits_{x \to x_0^-} f(x)=f(x_0)$$

Vidéo 1 - Continuité à gauche et continuité à droite

15 min

Voir la vidéo

Continuité en un point

Une fonction numérique $$f$$ est continue en $$x_0$$ si, et seulement si elle est continue à droite et à gauche au point $$x_0$$. En d'autres termes:

$$f$$ est continue au point $$x_0$$ $$\Leftrightarrow \lim\limits_{x \to x_0^-} f(x)= \lim\limits_{x \to x_0^+} f(x) =f(x_0)$$

Vidéo 2 - Continuité en un point et prolongement

15 min

Voir la vidéo

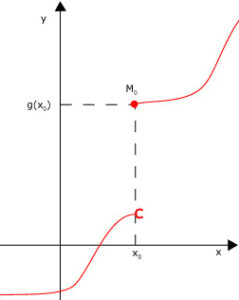
Prolongement par continuité en un point

تعريف

Soit $$f$$ une fonction numérique non définie en un point $$x_0$$ et admettant une limite finie $$l$$ en $$x_0$$:

$$ \lim\limits_{x \to x_0} f(x)=l \quad /~ l \in \mathbb{R}$$

Alors la fonction $$g$$ définie par:

$$\left\{\begin{array}{lcl} g(x)=f(x) ~~ ; ~~x \ne x_0 \\ g(x_0)=l \end{array} \right.$$

est continue en $$x_0$$, et est appelée le prolongement par continuité de $$f$$ au point $$x_0$$

Vidéo 3- Prolongement par continuité en un point

15 min

Voir la vidéo

Continuité d'une fonction sur un intervalle

تعريف

Une fonction $$f$$ est continue sur un intervalle ouvert $$I$$ si elle est continue en tout point de $$I$$
Une fonction est continue sur un intervalle fermé $$[a;b]$$ si elle est continue sur $$]a;b[$$ et continue à droite en $$a$$ et à gauche en $$b$$

مثال

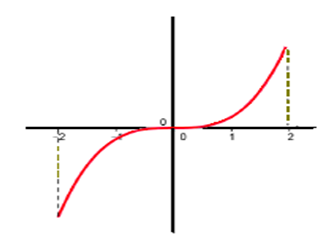
$$f$$ est une fonction définie sur l'intervalle $$I = [ – 2 ; 2 ]$$. Cette courbe se trace sans lever le crayon sur $$I$$ donc la fonction $$f$$ est continue sur: $$ I= [ – 2 ; 2 ]$$.

مثال

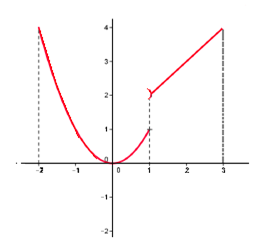
$$f$$ présente une "discontinuité" en $$x$$, si $$f$$ n'est pas continue en $$x$$. $$\\[0.2cm] f$$ est une fonction définie sur l'intervalle $$I = [– 2 ; 3]$$ sa courbe ne peut pas être tracée sans lever le crayon au point d'abscisse 1 donc la fonction $$f$$ n'est pas continue sur $$I = [– 2 ; 3]$$. (par contre elle est continue sur les intervalles $$[– 2 ;1]$$ et $$]1 ; 3]$$)

Le résultat important de cette section est le théorème des valeurs intermédiaires

نظرية

Théorème des Valeurs Intermédiaires: $$\\$$ Soit $$I$$ un intervalle de $$\mathbb{R}$$ et $$f$$ une fonction continue sur $$I\\$$ Soient: $$~m = inf\{ f(x), x \in I \}~$$ et $$~M = sup\{ f(x), x \in I \}\\$$ Si $$~m < M: ~$$ alors pour tout réel $$y$$ tel que $$~m < y < M$$,

$$\exists c \in I~$$ tel que $$~f(c) = y$$

ما يجب معرفته

Le résultat est tout à fait intuitif : si une fonction continue prend deux valeurs distinctes sur un intervalle, elle prend nécessairement toutes les valeurs entre ces deux-là, autrement dit: le graphe d'une fonction continue n'a pas de saut vertical.

خاصية

Si une fonction continue sur un intervalle prend des valeurs positives et des valeurs négatives, alors elle s'annule sur cet intervalle. On écrit:

$$f$$ est continue sur $$[a;b]~$$/ $$~f(a).f(b)<0~$$ $$~\Rightarrow ~$$ ( $$\exists \alpha \in [a;b])~$$ $$f(\alpha)=0$$

Si de plus la fonction $$f$$ est strictement monotone sur $$[a;b]$$, cette solution est unique et elle est définie sur $$]a;b[$$. On écrit:

( $$\exists! \alpha \in ]a;b[ )~$$ $$~f(\alpha)=0$$

ما يجب معرفته

Toute fonction polynomiale est continue sur $$\mathbb{R}$$
Les fonctions $$\sin(x)$$ et $$\cos(x)$$ sont continues sur $$\mathbb{R}$$
Toute fonction rationnelle est continue sur son domaine de définition.

Vidéo Continuité sur un intervalle

15 min

Voir la vidéo

Image d'un intervalle par une fonction continue

نظرية

L'image d'un intervalle par une fonction continue est un intervalle.

انتباه

Il est naturel de se demander si l'image par une application continue d'un intervalle est un intervalle du même type (infini, ouvert. . . ). Le seul résultat général concerne les intervalles fermés bornés (les segments).

نظرية

Soient $$ a < b $$ deux réels et $$f$$ une fonction continue sur $$[a, b]$$. Soit:

$$m = inf\{ f(x), x \in [a, b] \}~$$ et $$~M = sup\{ f(x), x \in [a, b] \}$$

Alors:$$~m~$$ et $$~M~$$ sont finies et il existe $$~x_1$$, $$x_2$$ $$\in [a, b], ~$$ tels que:

$$f(x_1) = m~$$ et $$~f(x_2) = M~$$ et $$~ f([a, b]) = [m, M]$$ .

Image d'un intervalle par une fonction continue et strictement monotone

نظرية

Soit $$f$$ une fonction continue, strictement monotone sur un intervalle $$I$$.

$$f(I)$$ est un intervalle, dont les bornes sont les limites de $$f$$ aux bornes de $$I$$ (pour plus de détails, regarder la vidéo du cours)
$$f$$ est une bijection de $$I$$ vers $$f(I)$$
la bijection réciproque $$f^{-1}$$ est continue sur $$f(I)$$ et strictement monotone et elle est de même sens que $$f$$.

L'image de l'intervalle $I$ par la fonction $f$

L'intervalle $I$	$f$ strictement croissante sur $I$	$f$ strictement décroissante sur $I$
$[a ,b]$	$[f(a) , f(b)]$	$[f(b) , f(a)]$
$]a ,b[$	$]\lim\limits_{x \to a^+}f(x) , \lim\limits_{x \to b^-}f(x)[$	$]\lim\limits_{x \to b^-}f(x) , \lim\limits_{x \to a^+}f(x)[$
$[a ,b[$	$[f(a) , \lim\limits_{x \to b^-}f(x)[$	$]\lim\limits_{x \to b^-}f(x), f(a)]$
$]- \infty , a]$	$]\lim\limits_{x \to -\infty}f(x) , f(a)]$	$[f(a) , \lim\limits_{x \to -\infty}f(x)[$
$]a , +\infty[$	$]\lim\limits_{x \to a^+}f(x) , \lim\limits_{x \to + \infty}f(x)[$	$]\lim\limits_{x \to + \infty}f(x) , \lim\limits_{x \to a^+ }f(x)[$
$\mathbb{R}$	$]\lim\limits_{x \to -\infty}f(x) , \lim\limits_{x \to +\infty}f(x)[$	$]\lim\limits_{x \to +\infty}f(x) , \lim\limits_{x \to -\infty}f(x)[$

Vidéo L'image d'un intervalle par une fonction continue

15 min

Voir la vidéo

Les opérations sur les fonctions continues

نظرية

Soient $$f$$ et $$g$$ deux fonctions continues sur un intervalle $$I$$ et $$k$$ un nombre réel. Alors :

Les fonctions $$f+g~,~ k.f$$, $$~f.g~$$ et $$~|f|~$$ sont continues sur $$I$$
Si la fonction $$g(x)$$ ne s'annule pas sur $$I~$$ alors $$~\frac{f}{g}~$$ est continue sur $$I$$
Si $$f(x)$$ est positive sur $$I~$$ alors $$~\sqrt{f}~$$ est continue sur $$I$$

ما يجب معرفته

Ce théorème permet de démontrer la continuité de toutes les fonctions que vous aurez à examiner, à condition d'admettre la continuité des "briques de base" que sont les fonctions usuelles. $\\[0.2cm]$ Toutes les fonctions usuelles sont continues en tout point où elles sont définies. Ceci concerne les fonctions puissances, exponentielle, logarithme, sinus, cosinus, mais exclut bien sûr la partie entière et la partie décimale.

continuité de la composée de deux fonctions

Soit $$f$$ une fonction définie sur un intervalle $$I$$ et $$g$$ une fonction définie sur un intervalle $$J$$ tels que $$~f(I) \subset J~$$ et $$~x_0 \in I$$.

Si $$f$$ est continue en $$x_0$$ et $$g$$ est continue en $$f(x_0)$$, alors la fonction $$g \circ f $$ est continue en $$x_0$$
Si $$f$$ est continue sur l'intervalle $$I$$ et $$g$$ est continue sur l'intervalle $$J$$ , alors la fonction $$g \circ f $$ est continue sur l'intervalle $$I$$.