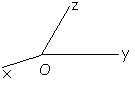Orientation de l'espace - trièdre - base et repères orientés
Repère de l'espace
تعريف
Un repère de l'espace est un quadruplet $(O, \vec{i}, \vec{j}, \vec{k})$ formé :
- D'un point $O$ appelé origine du repére.
- D'un triplet $(\vec{i}, \vec{j}, \vec{k})$ de vecteurs non coplanaires.
Trièdre
تعريف
Un trièdre est la figure formée par trois demi-droites non coplanaires de même origine. Les 3 plans $xOy$, $yOz$ et $zOx$ sont appelés les faces du trièdre. Si $Ox$, $Oy$, $Oz$ sont deux à deux perpendiculaires, le trièdre est dit trirectangle.
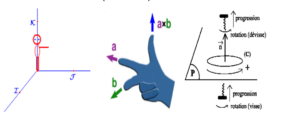
Le bonhomme d'Ampère
L'espace $(E)$ est muni d'un repère $(o;\vec{i};\vec{j};\vec{k})$ et $(\vec{i};\vec{j};\vec{k})$ la base qui lui est associée.
On pose un observateur (imaginaire) sur l'axe $[Oz)$ et il regarde vers $[Ox)$; on aura deux positions pour l'axe $[Oy)$.
1ère cas
$[Oy)$ est à droite de l'observateur.
On dit que la base $(\vec{i};\vec{j};\vec{k})$ est indirecte. De même pour le repère $(O; \vec{i}; \vec{j}; \vec{k})$.
2ème cas
$[Oy)$ est à gauche de l'observateur.
On dit que la base $(\vec{i};\vec{j};\vec{k})$ est directe. De même pour le repère $(O; \vec{i}; \vec{j}; \vec{k})$.
Bases directes
تعريف
Une base $(\vec{i}, \vec{j}, \vec{k})$ de $V_3$ est directe si le repère $(O, \vec{i}, \vec{j}, \vec{k})$ est direct quelque soit le point $O$ dans l'espace.
Produit vectoriel
تعريف
Soient $\vec{u}$ et $\vec{v}$ deux vecteurs dans $v_3$.
Le produit vectoriel des deux vecteurs $\vec{u}$ et $\vec{v}$ est le vecteur $~\vec{w}=\vec{u} \wedge \vec{v}$ tel que :
- Si $\vec{u}$ et $\vec{v}$ sont colinéaires alors : $~\vec{u} \wedge \vec{v}=\overrightarrow{0}$
- Si $\vec{u}$ et $\vec{v}$ sont non colinéaires :
- Le vecteur $~\vec{u} \wedge \vec{v}~$ est orthogonal à $\vec{u}$ et à $\vec{v}$
- La base $~(\vec{u}, \vec{v}, \vec{u} \wedge \vec{v})~$ est une base directe
- $\|\vec{u} \wedge \vec{v}\|=\|\vec{u}\| \cdot|| \vec{v}|| \sin \theta~$ où $~\theta~$ est la mesure de $\widehat{A O B}$
Remarque
- Le produit vectoriel de deux vecteurs est un vecteur, tandis que le produit scalaire de deux vecteurs est un réel.$\\$
- Si $~\vec{w}=\vec{u} \wedge \vec{v}~$alors $~\vec{u} \perp \vec{w}~$ et $~\vec{v} \perp \vec{w}\\$
- Si les vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux et unitaires alors la base $~(\vec{u} , \vec{v}, \vec{u} \wedge \vec{v} )~$ est une base orthonormée directe.
Les propriétés du produit vectoriel
Pour continuer cette fiche de cours, Inscris-toi gratuitement sur Kezakoo

- Fiches de cours illimitées
- Une vidéo gratuite par leçon
- 2 exercices gratuits par leçon
- Un test gratuit par leçon