Les deux photos montrent une balançoire pour enfant et la Grande Roue. Ces deux systèmes sont constitués par des corps solides qui ont un mouvement de rotation autour d’un axe fixe. Qu’est-ce qu’un mouvement de rotation ? Et quelles sont ses caractéristiques ?

Dans ce cours, on découvrira en particulier les mouvements de rotation dans le plan.
Rotation simple et réciproque
Définition
Soit un point du plan orienté positivement et un réel.La rotation de centre et d'angle est la transformation du plan notée ou qui vérifie :
Et pour tout point du plan différent de ; La rotation transforme un point en un point image tel que :
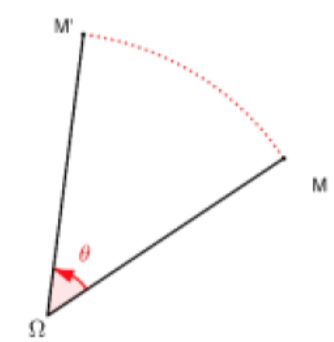
D'après la figure ci-dessus
Remarque
1. L'image du centre est (on dit que le point est invariant),
2. Les rotations d'angle sont appelées quarts de tour direct,
3. Les rotations d'angle sont appelées quarts de tour indirect,
4. La rotation de centre et d'angle est la symétrie centrale par rapport à .5. Si l'angle de la rotation est non nul, son centre est le seul point invariant.
Exemple
est un triangle. On construit à l'extérieur deux triangles et isocèles et rectangles en
1. Montrer que :
2. Montrer que :
Solution :
1- Soit la rotation de centre et d'angle On a : donc:
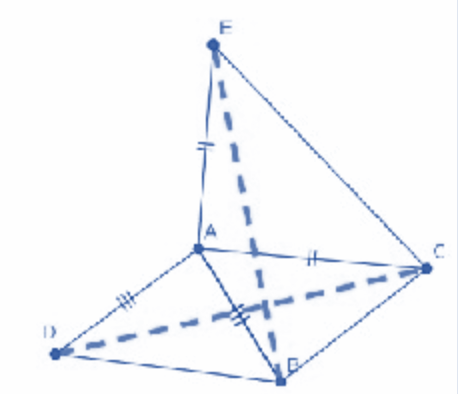
On a:
donc: Et puisque la rotation conserve les distances. Alors, on déduit que
2- on a et
Donc:
par suite :
Rotation réciproque
Définition
Soit une rotation de centre et d'angle . La rotation de centre et d'angle est appelée rotation réciproque de . On la note .
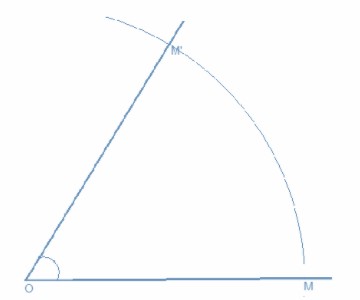
D'après la figure ci-dessus on a: .
Remarque
Soient et deux points du plan, si Alors
Caractéristiques et propriétés de la rotation
Pour continuer cette fiche de cours, Inscris-toi gratuitement sur Kezakoo

- Fiches de cours illimitées
- Une vidéo gratuite par leçon
- 2 exercices gratuits par leçon
- Un test gratuit par leçon


