Le produit scalaire est l'une des façons de combiner deux vecteurs. Nous calculons le produit scalaire de deux vecteurs et le résultat, son nom l'indique, est un scalaire plutôt qu'un vecteur.
Pour un peu d'histoire ,la notion du produit scalaire est apparue pour la première fois pour des besoins de la physique. Au milieu du XIXe siècle, le mathématicien allemand Hermann Grassmann a introduit le concept relativement récent.

Dans ce chapitre, vous apprendrez à calculer le produit scalaire de différentes manières et vous rencontrerez quelques concepts géométriques. Afin de maîtriser les techniques expliquées ici, nous commençons tout d'abord par un rappel.
Rappel
Produit scalaire de deux vecteurs
L’expression du produit scalaire en utilisant la projection orthogonale:
تعريف
Soient et et trois points dans le plan et la projection orthogonale du point sur la droite Alors le produit scalaire de est le nombre réel tel que
si et ont le même sens.
si et n'ont pas le même sens.
Si alors,
La formule trigonométrique du produit scalaire :
تعريف
Soient et deux vecteurs du plan, alors :
ما يجب معرفته
Le nombre réel positif est appelé la norme du vecteur
Et on note
خاصية
Linéarité du produit scalaire :
Symétrie du produit scalaire :
Positivité du produit scalaire :
Le produit scalaire est non dégénéré, c'est-à-dire :
et sont orthogonales :
Base orthonormée directe – Repère orthonormé directe
تعريف
On dit que le couple constitue une base du plan si : et sont deux vecteurs non colinéaires du plan. Et on dit que le plan est rapporté ou muni à la base ,
une base de et est un point de Le triplet s'appelle un repère de Et on dit que le plan est rapporté ou muni au repère est une base orthonormée si : et dans ce cas le repère est un repère orthonormé. est une base orthonormée directe si et seulement si : est une base orthonormée et Et dans ce cas le repère est un repère orthonormé directe.
Remarque
Dans toute la suite de ce cours, on considère le plan muni à un repère orthonormé directe
L’expression analytique du produit scalaire et la norme d’un vecteur dans un repère orthonormé directe
خاصية
Soient et deux vecteurs du plan , On a : 1. 2. 3.
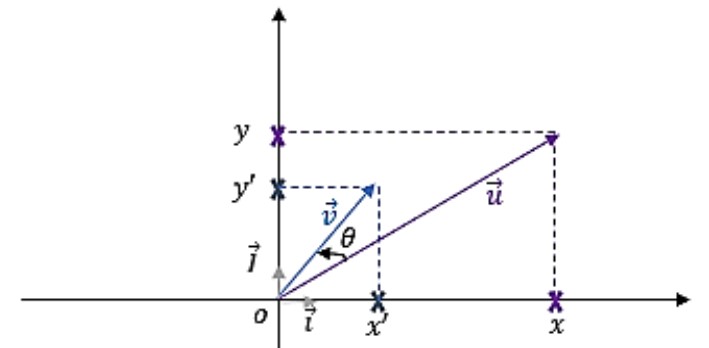
برهان
Car est orthonormé directe, donc :
D'après (1), on a et
مثال
On donne et et et 1. Calculons : 2. Calculons et 3. Calculons :
Formules de et
خاصية
Soient et deux vecteurs non nuls dans le plan, et , on a :
1.
2.
برهان
1. On a :
Donc :
2. Soit le vecteur tel que : et
Et on a
Donc :
Ou autrement :
مثال
Soient les trois points et
a- Calculons ,
On a :
Donc :
b- Calculons ,
On a :
Donc :
L’air d’un triangle et d’un parallélogramme
Pour continuer cette fiche de cours, Inscris-toi gratuitement sur Kezakoo

- Fiches de cours illimitées
- Une vidéo gratuite par leçon
- 2 exercices gratuits par leçon
- Un test gratuit par leçon