L’étude des fonctions numériques est importante dans tous les domaines des mathématiques pures et appliquées, y compris les mathématiques appliquées à l'économie, à la finance et aux affaires. Par exemple, le langage de l'analyse économique regorge de termes tels que les fonctions d'offre et de demande, les fonctions de coût, les fonctions de production et les fonctions de consommation.
Donc, dans ce chapitre, nous allons introduire quelques concepts majeurs tels que les asymptotes, les branches paraboliques, la convexité et l'axe de symétrie, qui nous sont utiles pour étudier le comportement de n'importe quelle fonction.
Asymptotes
Asymptote verticale
تعريف
Soit , lorsque ou .
La droite d'équation est une asymptote verticale à
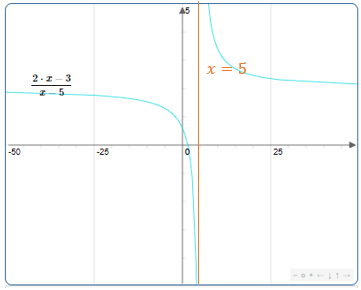
مثال
Soit la fonction définie par :
Déterminons et et interprétons géométriquement les résultats.
et
Alors et
Donc la droite d'équation est asymptote à .
Asymptote horizontale
تعريف
Soit , lorsque .
La droite d'équation est une asymptote horizontale à au voisinage de ou de .
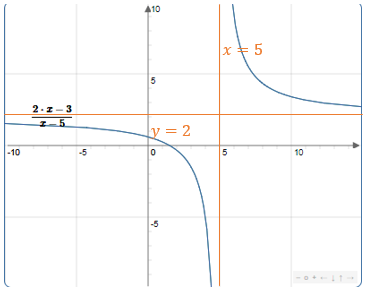
مثال
Soit la fonction définie par:
Déterminons ou et interprétons géométriquement les résultats.
et
Donc la droite est asymptote horizontale à .
Asymptote oblique
تعريف
Si tels que et .
Alors la droite d'équation est une asymptote à au voisinage de ou
مثال
Soit la fonction :
On a :
Et on a
Donc, est asymptote à .
حيلة
Soit la droite d'équation
est une asymptote à si et seulement si elle existe une fonction tel que :
et
مثال
Soit la fonction définie sur par :
On a donc la droite d'équation est une asymptote à au voisinage de
On a donc la droite d'équation est une asymptote à au voisinage de .
خاصية
La droite d'équation est une asymptote à si et seulement si :
et
ou :
et
حيلة
Pour étudier la position de par rapport à son asymptote il suffit d'étudier le signe de
مثال
Si on prend l'exemple précédent :
Si
Alors au-dessous de la droite
Si
Alors au-dessus de la droite
Branches paraboliques
Branches paraboliques de direction (OX) et (OY)
تعريف
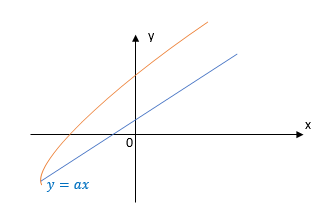
1. Si et
(ou et
On dit que présente une branche parabolique de direction asymptotique .
2. Si et
(ou et
On dit que présente une branche parabolique de direction asymptotique
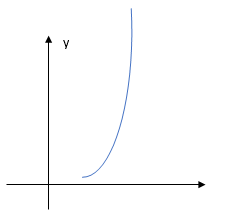
3. Si et et
(ou et et
On dit que la droite d'équation est une asymptote à au voisinage de (ou au voisinage de .
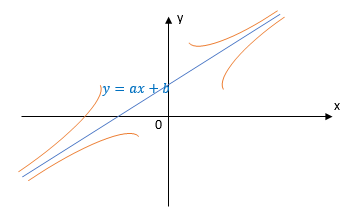
4. Si et
et
(ou et
et
on dit que admet une branche parabolique de direction la droite d'équation .
مثال
1. :
Et
Donc admet une branche parabolique de direction asymptotique au voisinage de
2.
Et
Donc admet une branche parabolique de direction asymptote au voisinage de
3.
On a
et
Et
Or
Donc admet une branche parabolique de direction la droite d'équation
Convexité – Point d’inflexion
Pour continuer cette fiche de cours, Inscris-toi gratuitement sur Kezakoo

- Fiches de cours illimitées
- Une vidéo gratuite par leçon
- 2 exercices gratuits par leçon
- Un test gratuit par leçon