Fiche de cours

La force électrostatique présente les même propriétés que la force gravitationnelle, à savoir qu'elle est conservative ce qui permet d'introduire tout naturellement les notions d'énergie et de potentiel électrostatique. La connaissance du potentiel suffit alors à décrire complètement les effets électriques.

  • QU’EST-CE QUE  LE TRAVAIL D’UNE FORCE ÉLECTROSTATIQUE UN CHAMP ÉLECTRIQUE UNIFORME ?
  • QU’EST-CE QU’UN POTENTIEL ÉLECTRIQUE?
  • QU’ELLE EST L’ENERGIE POTENTIELLE ÉLECTROSTATIQUE ?
  • CONSERVATION DE L’ENERGIE TOTALE D’UNE PARTICULE
  • CHARGÉE SOUMISE A UNE FORCE ELECTROSTATIQUE ?
  • ÉLECTRON-VOLT UNE AUTRE UNITÉ D’ÉNERGIE.

Rappel

Loi de Coulomb et Notion d’une force électrostatique

Mise en évidence

Deux charges électriques au repos q et q' s'attirent ou se repoussent mutuellement avec une force F :

  • Proportionnelle à chacune des charges Q et q'
  • Dirigée suivant la droite joignant les deux charges
  • Inversement proportionnelle au carré de la distance r qui les sépare

ما يجب معرفته

Lorsque les charges sont de même signe, le produit Qq' est positif et les forces d'interaction sont répulsives.

Lorsque les charges sont de signe opposé, le produit Qq' est négatif et les forces d'interaction sont attractives.

$\overrightarrow{F_{A B}}=-\overrightarrow{F_{B A}}=K \frac{q_{A} q_{B}}{d^{2}} \overrightarrow{u_{A B}}$

Avec k= coefficient de proportionnalité

$K=\frac{1}{4 \pi \varepsilon_{0}}=9 \times 10^{9} m^{3} \cdot K g \cdot s^{-2} \cdot C^{-2}$

Et on le vecteur champ électrostatique crée par une charge Q s’écrit :

$\vec{E}=K \frac{Q}{d^{2}} \vec{u}$

  • Direction : droite passante par le centre de la charge.
  • Sens : dépend du signe de la charge Q, centrifuge si Q>0, et centripète si Q<0
  • Module : $\mathrm{E}=\mathrm{K} \frac{Q}{d^{2}}$

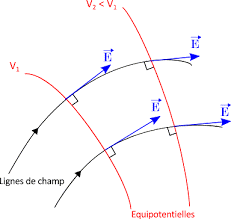
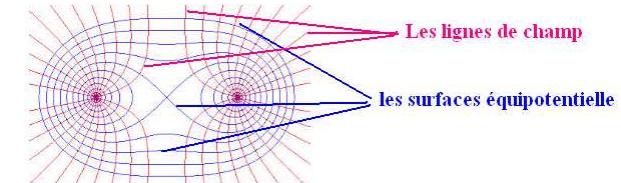
Lignes de champ électrostatique

On appelle ligne de champ, la ligne à laquelle le vecteur champ électrostatique est tangent en tout point.

superposition de champs électrostatique

Le vecteur champ électrique $\vec{E}$ crée par un ensemble de charges électriques est égale à la somme vectorielle des champs électriques  que crée chaque charge électrique  seule, et on a : $\vec{E}=\sum \overrightarrow{E_{1}}$

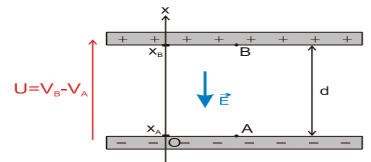
Travail de la force électrique dans un champ électrique uniforme

Activité

On place entre deux plaques parallélépipédique $P$ et $N$, un pendule électrostatique de charge q positive. Lorsqu’on applique une tension électrique entre les deux plaques, un champ électrostatique uniforme $E$ se crée et la charge $q$ se trouve soumise à une force électrique $\vec{F}$ =  q.$\vec{E}$ ce qui la déplace d’un point $A$ vers un point $B$.

Puisque le champ est uniforme donc la force  $\vec{F}$ est constante. Dans le repère orthonormé (O,$\vec{i}$, $\vec{j}$), trouver l’expression du travail de la force  $\vec{F}$ lorsque la charge se déplace de $A$ vers $B$ .

On sait que le travail de la force $\vec{F}$ au cours de déplacement de $A$ vers $B$ est:  

$\begin{aligned} W_{A B}(\vec{F}) &=\vec{F} \cdot \overrightarrow{A B} \\ W_{A B}(\vec{F}) &=q \vec{E} \times \overrightarrow{A B} \end{aligned}$

image/svg+xml Remarque

On sait que le travail de la force$\vec{F}$ au cours de déplacement de $A$ vers $B$ est:

$$W_{A B}(\vec{F})=q \vec{E} \times \overrightarrow{A B}$$

Dans le repère ($\vec{O}$,$\vec{i}$,$\vec{j}$):

$$\overrightarrow{A B}=\left(x_{B}-x_{A}\right) \vec{\imath}+\left(y_{B}-y_{A}\right) \vec{j}$$

et on a:

$\vec{E}=-E \vec{\imath}$

Donc:

$$W_{A B}(\vec{F})=q E\left(x_{A}-x_{B}\right)$$

Conclusion:

Le travail de la force électrique appliquée à une charge dans un champ électrique uniforme est indépendant du chemin suivi ; il ne dépend que de l'état initial XA et de l'état final XB. On dit que la force électrique est conservative.

Potentiel électrique

تعريف

Potentielle électrique:

On appelle $VA$ le potentiel électrique au point $A$. Le potentiel électrique est une grandeur physique qui caractérise l’état électrique de chaque point de l’espace où règne le champ électrique. Son unité en $SI$ est le volt : $V$

Potentiel d'un point d'un champ uniforme:

Le potentiel d'un point d'un champ uniforme d'abscisse $x$ s'écrit: $V=E.x$

Alors $V$ ne dépend que de la position du point et du champ électrique.

La différence de potentiel électrique:

La différence de potentielle ou tension électrique entre deux points A et B d’une région où règne un champ électrique uniforme $\vec{E}$, est égale au produit scalaire des vecteurs $\vec{E}$ et $\vec{AB}$:

$V_{A}-V_{B}=\vec{E} \times \overrightarrow{A B}$

image/svg+xml Remarque

  • Cette relation ne s’applique que si le champ électrique est uniforme.
  • Le champ $E$ est perpendiculaire aux surfaces équipotentielles et dirigé dans le sens de la décroissance de $V$ « c.-à-d. vers les potentiels décroissants » (à expliquer par suite).

Potentiel électrique

Dans le repère ($\vec{O}$,$\vec{i}$,$\vec{j}$) on a :

$V_{A}-V_{B}=\vec{E} \times \overrightarrow{A B}=E \times\left(X_{A}-X_{B}\right)$

De cette relation on constate que VA = E.x_{A} et VB = E.x_{B} On appelle VA le potentiel électrique au point $A$ et VB le potentiel électrique au point $B$. Le potentiel électrique est une grandeur physique qui caractérise l’état électrique de chaque point de l’espace où règne le champ électrique. Son unité en SI est V le volt D’où l’expression du travail de la force électrostatique :

$\begin{aligned} W_{A \rightarrow B}(\vec{F})=q E\left(x_{A}-x_{B}\right)=q E x_{A}-q E x_{B} \\ &=q\left(V_{A}-V_{B}\right)\end{aligned}$

image/svg+xml Remarque

  • Cette relation est valable même si le champ électrique n’est pas uniforme. Le travail de la force  est moteur signifie que :

VA −VB > 0 ⇒ VA > VB et le sens de   vers la plaque où le potentiel est petit.

  • les tensions sont représentées par des flèches allant du potentiel moins élevé vers le potentiel plus élevé.
  • Dans un champ uniforme, l'axe Ox est dirigé toujours dans le sens des potentiels croissants.
  • le vecteur champ électrostatique, est dirigé toujours du potentiel plus élevé vers potentiel moins élevé.

D’une façon générale:

Le sens du vecteur champ électrique $\vec{E}$ est dans le sens des potentiels décroissants.

Plan équipotentiel

Une surface (ou plan) équipotentielle électrique est une surface où la valeur du potentiel électrique est la même en tout point.

Les équipotentielles électriques possèdent les caractéristiques suivantes :

  • Le potentiel électrique est égal en tout point de la surface.
  • Le champ électrique est perpendiculaire à la surface équipotentielle.
  • Le sens du champ électrique définit le sens où il y a une chute de potentiel.

image/svg+xml Remarque

Les plans équipotentiels sont des plans parallèles entre eux et perpendiculaire au vecteur champ électrique $\vec{E}$.

مثال

  • Deux plaques parallèles:

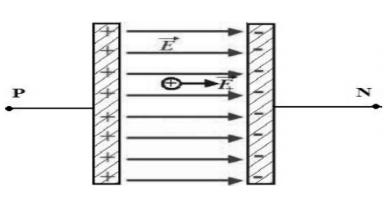
Lignes de champ électrostatiques uniforme :

Le champ électrostatique est toujours dirigé de la plaque positive vers la plaque négative, et les lignes de champs sont toujours parallèles.

 

  • Les charges ponctuelles:

  • Un doublet formé par ne charge positive et une charge négative:

Énergie potentielle électrostatique

لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

النسخة المجانية لكيزاكو:
  • ملخصات الدروس غير محدودة
  • فيديو مجاني في كل درس
  • تمرين مصحح مجاني
  • اختبار تفاعلي
إنشاء حساب مجاني
Signaler une erreur
Energie potentielle d’une charge électrique dans un champ électrostatique uniforme
Sommaire du cours
Signaler une erreur