Les images formées par une lentille mince convergente

Après l’étude du miroir plan qui intervient quelque fois dans les instruments d’optique, nous allons voir un des composants essentiels des instruments, les lentilles. La plus « simple » d’entre elles est la lentille convergente, c’est celle que nous étudions ici.  On va voir comment, par des schémas géométriques, on peut modéliser l’action d’une lentille convergente sur la lumière. Nous verrons également que pour utiliser ces lentilles en pratique, il convient de connaître certaines grandeurs qui leur sont associées, et de les utiliser dans des relations mathématiques.

→ Qu’est-ce qu’une lentille mince convergente ?

→ Quelles sont les caractéristiques des lentilles minces convergentes ?

→ Image formée par une lentille convergente.

→ Description de l’image pour différentes positions de l’objet.

→ Les relations de conjugaison et de grandissement.

Généralités sur les lentilles minces

Les différents types de lentilles

Il existe deux types de lentilles minces différentiables aux toucher ou par le biais de méthodes expérimentales que nous n’étudierons pas ici (hors programme).

• On distingue les lentilles dites :

⇒ Convergentes à bords minces que l’on schématise ainsi :

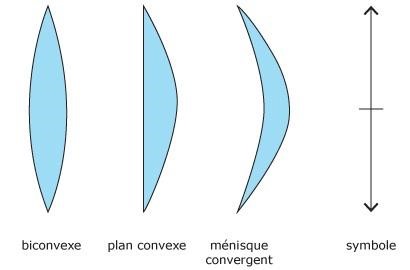
⇒ Divergentes à bords épais que l’on schématisera de cette manière :

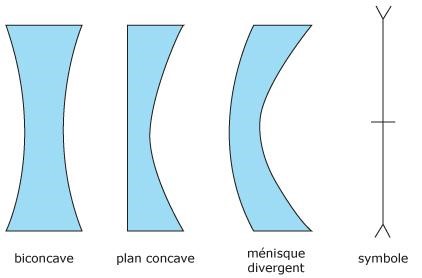
Effet d'une lentille convergente sur un faisceau lumineux

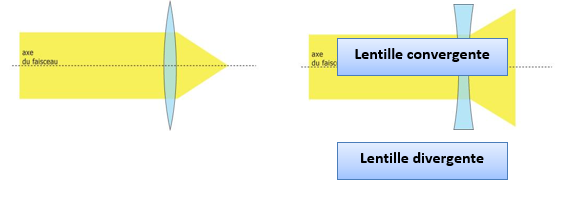
→ Les lentilles convergentes transforment le faisceau parallèle de la lampe en un faisceau convergent en un point.

→ Les lentilles divergentes font diverger, c'est-à-dire s'écarter, le faisceau et on observe une grosse tache lumineuse.                       

                                   

Caractéristiques des lentilles minces convergentes

L'axe optique principal – le centre optique

Approche expérimentale

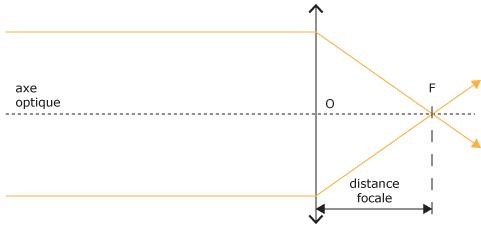
Plaçons une lentille convergente entre le soleil et une feuille de papier. Il existe une distance lentille-feuille qui permet de visualiser un point lumineux sur la feuille qui peut s’enflammer si on poursuit suffisamment longtemps l’expérience.

⇒ Cette distance est appelé distance focale. Elle sépare la lentille de son foyer (F), point sur l’axe optique où tous les rayons lumineux convergent.

On définit O, le centre optique comme le point d’intersection entre l’axe optique et la lentille.

انتباه

• Les rayons lumineux qui passent par O ne sont jamais déviés.
• Si l'objet se trouve dans l'espace objet il est réel et s'il se trouve dans l'espace image il est virtuel.
•  Si l'image se trouve dans l'espace image elle est réelle et si elle se trouve dans l'espace objet elle est virtuelle.

Foyer principal image et Foyer principal objet

Lorsqu’un miroir, Une lentille convergente comporte deux foyers, appelés foyer principal objet et foyer principal image :

→ Tout rayon incident parallèle à l’axe optique émerge en passant par F’, foyer principal image. Ce foyer est donc l’image d’un objet à l’infini.

→ Tout rayon incident passant par F, foyer principal objet, émerge parallèle à l’axe optique. Ce foyer a donc son image à l’infini.

→ Ces foyers sont symétriques par rapport au centre optique de la lentille.

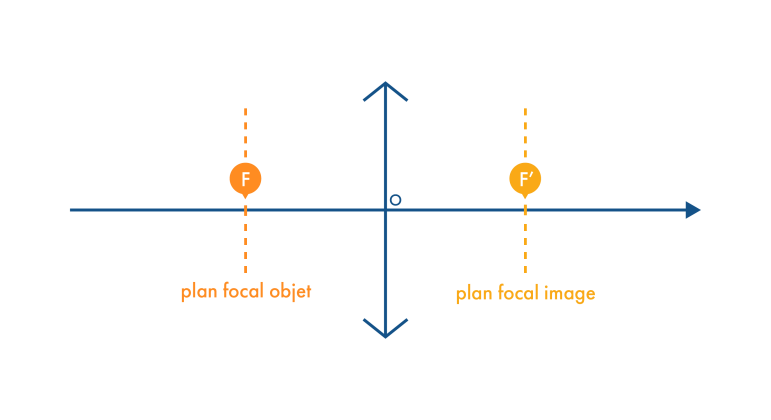
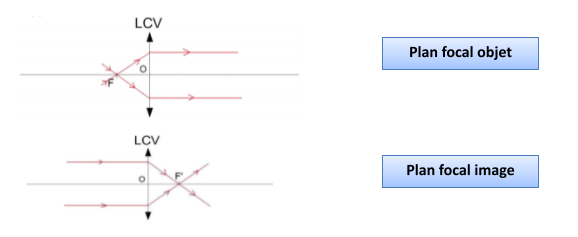
• Les foyers F et F’ sont symétriques par rapport au centre optique.

Distances focales

⇒ On appelle distance focale objet la grandeur f OF (f   0 pour une lentille convergente et |f|=f ’). 

⇒ On nomme distance focale image (utilisée en pratique) la grandeur f1 OF 1 mesurée sur l’axe optique orienté dans le sens de propagation de la lumière (f’¡0 pour une lentille convergente).

Vergence d’une lentille convergente

Image formée par une lentille convergente