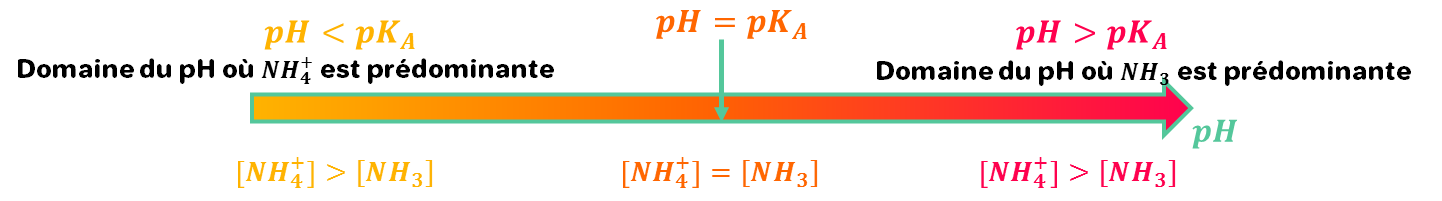Partie 1

1.1 Montrer que la concentration molaire effective des ions ammonium $$N H_{4(a q)}^{+}$$à l’état d’équilibre du système est donnée par la relation: $$ \left[N H_{4(a q)}^{+}\right]_{eq}=\frac{K_{e}}{10^{-p H}}$$. Calculer sa valeur.

D’après le tableau d’avancement :

$$ \begin{gathered} {\left[N H_{4}^{+}\right]_{k q}=\left[H O_{(a q)}^{-}\right]_{e q}=\frac{x_{e q}}{V_{0}}} \\ {\left[H O^{-}\right]_{\varepsilon q} \cdot\left[H_{3} O^{+}\right]_{e q}=K e \rightarrow\left[H O^{-}\right]_{e q}=\frac{K e}{\left[H_{3} O^{+}\right]_{e q}}=\frac{K e}{10^{-p H}}} \\ {\left[N H_{4}^{+}\right]_{i q}=\frac{K e}{10^{-p H}}=\frac{10^{-14}}{10^{-p H}}=3,98.10^{-4} \mathrm{~mol} . L^{-1}=4.10^{-4} \mathrm{~mol} . L^{-1}} \end{gathered} $$

1.2 Calculer la valeur du quotient de réaction $$Q_{r, \text { éq }}$$du système chimique à l’équilibre. En déduire la valeur de la constante d’équilibre K associée à l’équation de la réaction.

$$ \begin{gathered} Q_{r, e q}=\frac{\left[N H_{4)}^{+}\right]_{e \dot{q}^{\cdot}}\left[H O_{(a q)}^{-}\right]_{e \dot{e} q}}{\left[N H_{3}\right]_{\dot{e} q}} \\ {\left[N H_{3}\right]_{\dot{e} q}=\frac{C_{0} V_{0}-x_{\dot{e} q}}{V_{0}}=C_{0}-\frac{x_{\dot{e} q}}{V_{0}}=C_{0}-\left[H{O}_{(a q)}^{-}\right]_{\dot{e} q}} \\ Q_{r, e q}=\frac{\left[H o_{(a q)}^{-}\right]_{e q}^{2}}{C_{0}-\left[H O_{(a q)}^{-}\right]_{\dot{e} q}}=\frac{4.10^{-4}}{1.10^{-2}-4 \cdot 10^{-4}}=K=1,65 \cdot 10^{-5} \end{gathered} $$

1.3 La constante d’acidité du couple $$\left(N H_{4(a q)}^{+} / N H_{3(a q)}\right)$$ s’exprime par : $$K_{A}=\frac{K_{e}}{K}$$

Calculer le $$p K_{A} $$ de ce couple.

$$ \left\{\begin{array}{l} p K_{A}=-\log K_{A} \\ K_{A}=\frac{K_{e}}{K} \end{array} \rightarrow p k_{A}=-\log \left(\frac{K_{e}}{K}\right) \rightarrow p K_{A}=-\log \left(\frac{10^{-14}}{1,65 \cdot 10^{-5}}\right)=9,2 \mid\right. $$

1.4 Tracer le diagramme de prédominance des espèces du couple $$ \left(N H_{4(a q)}^{+} / N H_{3(a q)}\right) $$. En déduire l’espère prédominante de ce couple dans le mélange.

$$ p H=6,2 ; p K_{A}=9,2 \rightarrow p H<p K_{A} \rightarrow N H_{4}^{+} $$ est l’espère prédominante de ce couple dans le mélange.

2.1 Ecrire l’équation de la réaction qui se produit entre les ions ammonium $$N H_{4(a q)}^{+}$$ et les ions hydroxyde $$H O_{(a q)}^{-}$$ au cours du dosage, sachant qu’elle est totale.

$$ \mathrm{NH}_{4(a q)}^{+}+\mathrm{HO}_{(a q)}^{-} \rightarrow N H_{3(a q)}+\mathrm{H}_{2} \mathrm{O}_{(l)} $$

2.2 Déterminer la valeur de la concentration molaire $$C_{A}$$ des ions ammonium $$N H_{4(a q)}^{+}$$ dans la solution $$\left(S_{A}\right)$$.

$$ \begin{gathered} C_{A} \cdot V_{A}=C_{E} \cdot V_{B E} \\ C_{A}=\frac{C_{B} \cdot V_{B E}}{V_{A}}=\frac{0,1 \times 14.10^{-3}}{10.10^{-3}}=0,14 \mathrm{~mol} . L^{-1} \end{gathered} $$

2.3 Le pourcentage massique en nitrate d’ammonium contenu dans cet engrais s’exprime par la relation :

$$\frac{m\left(N H_{4} N O_{3}\right)}{m}$$ avec la masse de l’engrais.

Calculer le pourcentage massique en masse de nitrate d’ammonium contenu dans cet engrais. Comparer à la valeur annoncée par le fabriquant.

$$ \begin{gathered} C_{A}=\frac{n}{V_{0}}=\frac{m\left(N H_{4} N O_{3}\right)}{M\left(N H_{4} N O_{3}\right) \cdot V_{0}} \\ m\left(N H_{4} N O_{3}\right)=C_{A} \cdot M\left(N H_{4} N O_{3}\right) \cdot V_{8} \\ m\left(N H_{4} N O_{3}\right)=0,14 \times 80 \times 1 \\ m\left(N H_{4} N O_{3}\right)=11,2 g \\ x=\frac{11,2}{15}=0,747 \approx 75 \% \end{gathered} $$

→Semblable au le pourcentage massique en nitrate d’ammonium indiqué par le producteur.

Partie 2

1. Ecrire l’équation de la réaction de fonctionnement de la pile.

Au voisinage de la cathode : (Réduction)

$$ \mathrm{Cu}^{2+}+2 e^{-} \rightleftarrows \mathrm{Cu} $$

Au voisinage de l’anode : (Oxydation)

$$ \mathrm{Ni} \rightleftarrows \mathrm{Ni}^{2+}+2 e^{-} $$

L’équation de la réaction de fonctionnement de la pile :

$$ \mathrm{Cu}^{2+}+\mathrm{Ni} \rightleftarrows \mathrm{Cu}+\mathrm{Ni}^{2+} $$

2. Calculer $$Q_{\max }$$ la quantité d’électricité maximale débitée par la pile.

$$ \begin{gathered} n_{i}\left(C u^{2+}\right)-x_{\max }=0 \\ x_{\max }=n_{i}\left(C u^{2+}\right) \\ n\left(e^{-}\right)=2 x_{\max }=\frac{Q_{\max }}{F} \\ Q_{\max }=2 x_{\max } \cdot F=2 \times 1.10^{-2} \times 9,65 \cdot 10^{4}=1930 C \end{gathered} $$

3. Déterminer la durée de vie $$\Delta t$$ de cette pile.

$$ Q_{m}=I . \Delta t \rightarrow \Delta t=\frac{Q_{m}}{I}=\frac{1930}{40.10^{-3}}=48250 \mathrm{~s}=13 \mathrm{~h} 24 \mathrm{~min} 10 \mathrm{~s} $$