1. La valeur du quotient de réaction $Q_{r, i}$ dans l’état initial du système chimique. 

Equation de la réaction :

$N i_{(a q)}^{2+}+C d_{(s)} \rightleftarrows N i_{(s)}+C d_{(a q)}^{2+}$

L’expression du quotient de réaction :

$Q_{r, i}=\frac{\left[C d^{2+}\right]_{i}}{\left[N i^{2+}\right]_{i}}=\frac{C}{C}=1$

On a :

$Q_{r, i}<K=4,5.10^{5}$ L’ensemble évolue spontanément dans le sens direct ( sens de formation de Ni et $\boldsymbol{C d}^{2+}$

2. Le schéma conventionnel de cette pile.

Au niveau de la cathode se produit la réduction donc l’électrode de 𝑁𝑖 représente le pôle positif de la pile. Le schéma conventionnel est :

$(+) N i_{(s)} / N i_{(a q)}^{2+} \therefore C d_{(a q)}^{2+} / C d_{(s)}(-)$

L’équation de la réaction à chaque électrode :

Au niveau de la cathode (électrode de nickel) se produit la réduction des ions $N i^{2+}$:

$N i_{(a q)}^{2+}+2 e^{-} \rightleftarrows N i_{(s)}$

Au niveau de l’anode (électrode de cadmium) se produit l’oxydation de $\boldsymbol{C d}_{(s)}$:

$C d_{(s)} \rightleftarrows C d_{(a q)}^{2+}+2 e^{-}$

4. La variation $\Delta \mathbf{m}$ de la masse du nickel pendant $\boldsymbol{\Delta} \mathbf{t}$:

Tableau d’avancement de la réaction de réduction :

D’après le tableau :

$\begin{gathered} \left\{\begin{array}{c} \Delta n(N i)=x \\ n\left(e^{-}\right)=2 x \end{array} \rightarrow \Delta n(N i)=\frac{n\left(e^{-}\right)}{2} \rightarrow \frac{\Delta m}{M(N i)}=\frac{I . \Delta t}{2 F} \rightarrow \Delta m=\frac{I \Delta t}{2 F} \cdot M(N i)\right. \\ \Delta m=\frac{0,3 \times 5 \times 3600}{2 \times 9,65.10^{4}} \times 58,7 \rightarrow \Delta m=1,64 g \end{gathered}$

Partie 2

1. L’équation de la réaction de dosage. 

$\mathrm{AH}_{(a q)}+\mathrm{HO}_{(a q)} \rightarrow \mathrm{A}_{(a q)}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}$

2. Pour obtenir l’équivalence, on doit verser le volume $V_{B E}=10 m L$ de la solution SB.        

2.1. La concentration $\boldsymbol{C}_{A}$de la solution S :

D’après la relation d’équivalence :

$C_{A} \cdot V_{A}=C_{B} \cdot V_{B E} \text { d'où }: C_{A}=C_{B} \cdot \frac{V_{B E}}{V_{A}}$

A.N : $C_{A}=\frac{10^{-2} \times 10}{10} \Rightarrow C_{A}=10^{-2} \text { mol. } L^{-1}$        

2.2. Montrer que m = 0,5 g.

$\begin{aligned} &\text { On a : } C_{A}=\frac{n}{V}=\frac{m}{M\left(C_{9} H_{\mathrm{s}} O_{4}\right) \cdot V} \text { alors: } m=C_{A} \cdot M\left(C_{9} H_{8} O_{4}\right) \cdot V \\ &\text { A.N : } m=10^{-2} \times 180 \times 278.10^{-3}=0,5 \mathrm{~g} \end{aligned}$

3. Parmi les indicateurs colorés dans le tableau ci-dessous, l’indicateur convenable à ce dosage. 

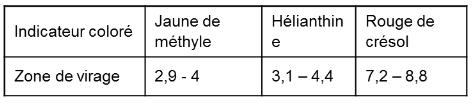
L’indicateur coloré convenable est celui dont la zone de virage contient $p H_{E}$.

D’après l’équation de la réaction, à l’équivalence, le mélange réactionnel contient les ions $A^{-}$ et l’eau, donc le milieu est basique et son $\mathrm{pH}>7$.