Dans la vie de tous les jours, on est toujours tendance a faire des travaux comme bien évidement :
- Soulever une bouteille d’eau ;
- Marcher/ faire du sport, etc.…
→ Au cours de nos travaux on fournit des efforts par habitude. On les appelle travail et puissance, mais en physique ces notions ont des significations bien déterminées.
On s’interroge alors :
- Qu'est-ce que le travail mécanique ?
- Qu'est-ce que la puissance mécanique ?
- Quelle relation existe-t-elle entre le travail et la puissance ?
Rappel
Notion d’une force
On modélise toute action mécanique par une grandeur vectorielle, appelée vecteur-force F caractérisée par :
√ son point d’application ;
√ sa direction ;
√ son sens ;
√ et son intensité en Newton dans SI.
Les effets mécaniques d’une force sur un corps mécanique
La force a plusieurs effets mécaniques sur un corps solide parmi ses effets, on trouve :
- Provoquer le mouvement d’un corps solide ;
- Provoquer le mouvement de rotation ;
- Déformer un corps solide.
Notion d’une force constante
On place Une force est dite constante, lorsque sa valeur, sa direction et son sens ne varient pas au cours du temps
مثال
- Le poids d’un corps solide ;
- La tension d’un fil inextensible ;
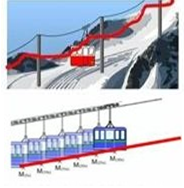
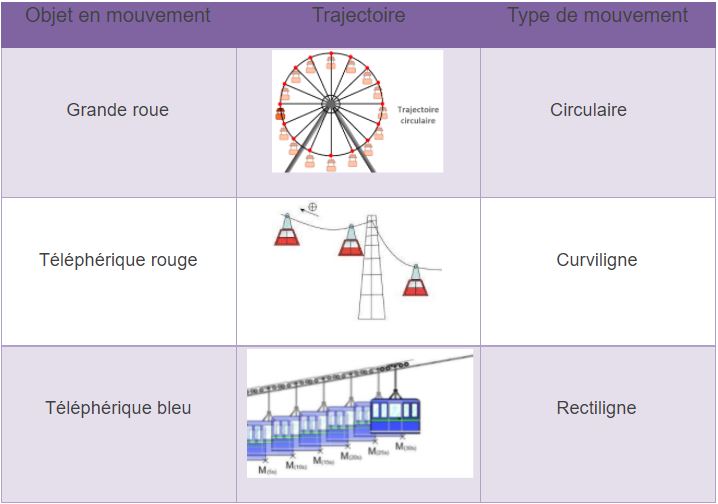
Notion de mouvement de translation rectiligne et curviligne et circulaire
-
- Mouvement de translation rectiligne : la trajectoire de chaque point du solide est une droite.
- Mouvement de translation curviligne : la trajectoire de chaque point du solide est une courbe.
- Mouvement de translation circulaire : La trajectoire de chaque point du solide est un cercle
Travail d’une force ou un ensemble des forces
Travail d’une force constante exercée sur un corps solide en translation rectiligne
تعريف
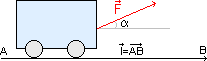
On considère un corps solide S en translation rectiligne, et M un point appartenant a S, soumis a une force constante. On appelle travail de la force F, dont le point d’application se déplace d’une position A a une autre position B, le produit scalaire du vecteur force F et de vecteur de déplacement AB, ce travail est noté :
Unité du travail
L’unité du travail dans le système international est : le Joule (J)
تعريف
Définition du joule :
le joule et le travail fournit par une force d'intensité 1N, Lorsque sont point d'application se déplace de 1m selon sa direction et son sens
Remarque
On peut aussi exprimer le travail d’une force constante en utilisant les coordonnées des deux vecteurs F et AB dans un repère orthonormé R (o, i, j)
Travail moteur, travail résistant, travail nul
⇒ Travail moteur :
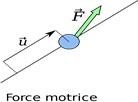
Pour mettre en mouvement et augmenter la vitesse d’un chariot tout le long d’un plan incliné on le pousse dans le même sens du déplacement dans ce cas la force exercée est motrice, dans ce cas
Remarque
Lorsque la force est parallèle et de même sens que le déplacement, on a et le travail est maximal.
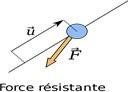
⇒ Travail résistant :
Lorsqu’on veut ralentir le chariot, il faut exercer une force F en sens contraire du mouvement, la force est alors résistance. Dans ce cas :
Remarque
Lorsque la force est parallèle et de sens oppose que le déplacement, on a , et le travail est minimal.
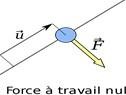
⇒ Travail nul
Lorsque la force F agit perpendiculairement au déplacement AB, l’angle α=90, cos(α)=0 on dit que la force n’effectue aucun travail.
Remarque
Le travail est, il peut être négatif comme il peut être une grandeur algébrique positif.
Travail d’une force constante exercée sur un corps solide en translation curviligne
Notion de travail élémentaire
On considère le point M d’un solide (S) comme point d’application de la force constante, le solide (S) est en translation curviligne et la trajectoire de M est une courbe.
- Quelle est l’expression du travail de la force F dans ce cas ?
Pour cela on devise la trajectoire en morceaux infiniment petits qu’on peut l’assimiler a des arcs.
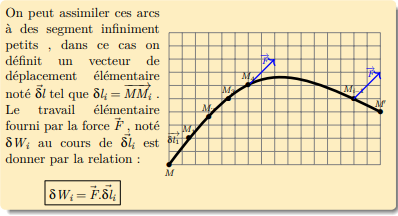
Travail d’une force constante exerce sur un solide en translation curviligne
Travail d’un ensemble de forces constantes exercés sur un corps en translation

le travail fournit par un ensemble de forces constantes exercées sur un corps solide en translation (rectiligne ou curviligne) est égale au déplacement AB
Travail du poids d’un corps solide
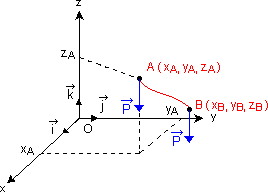
Pour un corps se déplaçant près du sol. Le poids du corps est une force constante. L'expression du travail du poids au cours du déplacement de centre de gravité Ga a Gb s'écrit alors :
On choisit un axe (OZ) vertical dirigé vers le haut et comme :
Dans un repère (tel que dirigé vers le haut) les cordonnées de et sont :
et
donc
Conclusion:
Le travail du poids d'un corps solide ne dépend pas du chemin parcouru par le centre d'inertie il dépend seulement de l'altitude ZA Du point de départ et de l'altitude ZB du point d'arrivée on dit que le poids est une force conservative.
Remarque
Dans le cas où le déplacement s'effectue du haut vers le bas, donc le travail du poids est moteur.
Dans le cas où le déplacement s’effectue du bas vers le haut, donc le travail du poids est résistant.
Travail d’une force de moment constant exerce sur un corps solide en rotation autour d’un axe fixe
لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

- ملخصات الدروس غير محدودة
- فيديو مجاني في كل درس
- تمرين مصحح مجاني
- اختبار تفاعلي
- Rappel
- Travail d’une force ou un ensemble des forces
- Travail d’une force de moment constant exerce sur un corps solide en rotation autour d’un axe fixe