-
-
Maths
La géométrie dans l'espace
2ème année bac Sciences Physiques Maths La géométrie dans l espace fiche de cours
Le produit scalaire dans l'espace :
تعريف
L'espace est rapporté à un repère $(o ; \vec{i} ;\vec{j} ; \vec{k}) \\[0.2cm]$ Soient $\vec{u}(x ; y ;z)$ et $\vec{v}(x' ; y'; z')$ deux vecteurs de l'espace. $\\[0.2cm]$ Alors le produit scalaire des vecteurs $\vec{u}$ et $\vec{v}$ est $\\$
$\vec{u} \cdot \vec{v} = xx' + yy' + zz'$
Remarque
On a $~~\vec{u} \cdot \vec{v}=||\vec{u}||\times ||\vec{v}|| \times \cos (\widehat{\vec{u} , \vec{v}})\\[0.2cm]$ Avec $~~||\vec{u}||=\sqrt{x^2 +y^2 +z^2} $
تطبيق
Calculer $~\vec{u} \cdot \vec{v} ; ||\vec{u}||$ et $||\vec{v}|| \\[0.2cm]$ Avec $~\vec{u} (2 ; 0 ; 1)$ et $~\vec{v} (-1 ; 3 ; 0)\\[0.3cm]$ $\vec{u} \cdot \vec{v} = 2 \cdot (-1)+0 \cdot 3+2 \cdot 0=-2 \\[0.2cm]$ $||\vec{u}||= \sqrt{2^2 +0^2 +1^2}=\sqrt{5} \\[0.2cm]$ $||\vec{v}||=\sqrt{(-1)^2 + 3^2 + 0^2}$
تطبيق
Calculer $\overrightarrow{AB} \cdot \overrightarrow{AC}$ si $A(1 ; 2 ; 0)$ et $B(-1 ; 4 ; 1)$ et $C(2 ; -1 ; -1) \\[0.3cm]$ Tout d'abord $~\overrightarrow{AB}(x_B -x_A ;~ y_B -y_A ; ~z_B -z_A) \\[0.2cm]$ Donc $~\overrightarrow{AB}(-2 ; 2 ; 1) \\[0.2cm]$ Et de même $~\overrightarrow{AC}(1; -3 ; -1) \\[0.2cm]$ D'où $~\overrightarrow{AB} \cdot \overrightarrow{AC}=(-2) \cdot 1 +2 \cdot (-3)+1 \cdot (-1)=-9$
خاصية
- On dit que les vecteurs $\vec{u}$ et $\vec{v}$ et $\vec{w}$ sont coplanaires si et seulement si, il existe deux réels $\alpha$ et $\beta$ tels que : $~\vec{w}= \alpha \cdot \vec{u}+ \beta \cdot \vec{v} \\[0.2cm]$
- Les vecteurs $\vec{u}$ et $\vec{v}$ et $\vec{w}$ sont coplanaires si et seulement si : $~\det (\vec{u} ; \vec{v} ; \vec{w})=0$
La distance entre deux points :
تعريف
Soient $~A(x_A ; ~y_A ; ~z_A) ~$ et $~B(x_B ; ~y_B ; ~z_B) \\[0.2cm]$ La distance entre $A$ et $B$ est
$AB= ||\overrightarrow{AB}||=\sqrt{(x_B-x_A)^2 +(y_B-y_A)^2 +(z_B-z_A)^2}$
Les coordonnées du milieu d'un segment :
تعريف
Soient $I$ le milieu du segment $[AB]\\[0.2cm]$ Alors les coordonnées de $\overrightarrow{AI}$ sont :
$\begin{aligned} \overrightarrow{AI}=\frac{1}{2}\overrightarrow{AB}~ &\left\{\begin{array}{ll} x_I -x_A=\frac{1}{2} (x_B - x_A ) \\[0.2cm] y_I -y_A=\frac{1}{2} (y_B - y_A ) \\[0.2cm] z_I -z_A=\frac{1}{2} (z_B - z_A )\end{array} \right. \\[0.2cm] &\left\{\begin{array}{ll} x_I =\frac{1}{2} (x_B + x_A ) \\[0.2cm] y_I =\frac{1}{2} (y_B + y_A ) \\[0.2cm] z_I =\frac{1}{2} (z_B + z_A )\end{array} \right. \end{aligned} $
Plan défini par un point et un vecteur normal
Vecteur normal à un plan :
تعريف
Le vecteur non nul $\vec{n}$ est normal à un plan $(\mathcal{P})$ si et seulement si le vecteur $\vec{n}$ est orthogonal à deux vecteurs directeurs de $(\mathcal{P})$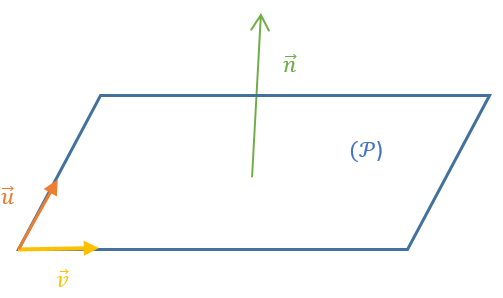
مثال
On considère $~A(3 ; -2 ; 2)$,$B(6 ; 1 ; 5)$, $C(6 ; -2 ; -1)$ et $D(0 ; 4 ; -1) \\[0.2cm]$ Montrer que $~(AD) \perp (ABC) $
$\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont 2 vecteurs directeurs de $(ABC)\\[0.2cm]$ On a $~\left\{\begin{array}{ll}\overrightarrow{AD} (-3 ; 6 ; -3 )\\ \overrightarrow{AB} (~3 ; ~3 ; ~3 ) \\ \overrightarrow{AC} (~3 ; ~0 ; -3 )\end{array}\right. \\[0.2cm]$ On a : $~\overrightarrow{AD} \cdot \overrightarrow{AC}=-3 \cdot 3 +6 \cdot 0+(-3) \cdot (-3)=0 \\[0.2cm]$ Et $~\overrightarrow{AD} \cdot \overrightarrow{AB}=-3 \cdot 3 +6 \cdot 3+(-3) \cdot 3=0 \\[0.2cm]$ Donc $~(AD) \perp (AB)~$ et $~(AD) \perp (AC)\\[0.2cm]$ D'où $~(AD) \perp (ABC)$
Equation cartésienne d'un plan défini par un point et un vecteur normal:
تعريف
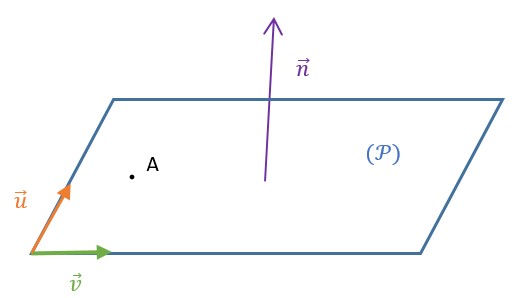
Soit $\vec{n}(a ; b ; c)$ un vecteur non nul et $A$ un point de l'espace $\\[0.2cm]$ Le plan $(\mathcal{P})$ passant par $A$ et de vecteur normal $\vec{n}$, est l'ensemble des points $M$ tel que : $\overrightarrow{AM} \cdot \vec{n}=0~~$ avec $~M(x ; y ; z) \\[0.2cm]$ Donc l'équation cartésienne de $(\mathcal{P})$ est : $~ax+by+cz+d=0 ~~$ avec $~d\in \mathbb{R} \\[0.3cm]$ Inversement, l'ensemble des points $M$ tel que $\overrightarrow{AM} \cdot \vec{n}=0$ est le plan passant par $A$ et de vecteur normal $\vec{n}$
مثال
Déterminer l'équation cartésienne du plan $(\mathcal{P})$ de vecteur normal $\vec{n}(1 ; -1 ; 3)$ et passant par $A(2 ; -1 ; 1) \\[0.3cm]$ On a $~(\mathcal{P}):~1 \cdot x +(-1) \cdot y +3 \cdot z+d=0 ~~$ avec $d \in \mathbb{R} \\[0.2cm]$ D'où $~~ (\mathcal{P}):~ x-y+3z+d=0 \\[0.2cm]$ Déterminons $d : \\[0.2cm]$ Puisque $A \in (\mathcal{P})~$ alors : $~x-y+3z+d=0 \\[0.2cm]$ Donc $~2+1+3+d=0 ~~$ c à d : $~d=-6 \\[0.2cm]$ D'où $~~(\mathcal{P}):~x-y+3z-6=0 \\[0.2cm]$
Orthogonalité de deux plans
خاصية
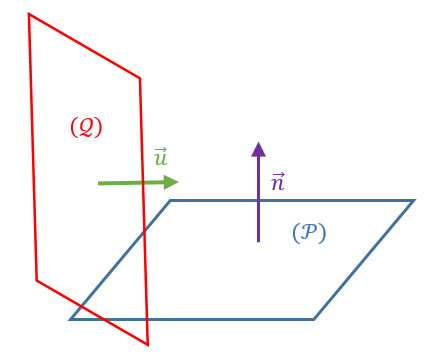Soit $\vec{n}$ un vecteur normal au plan $(\mathcal{P}) \\[0.2cm]$ Soit $\vec{u}$ un vecteur normal au plan $(\mathcal{Q}) \\[0.2cm]$ Les plans $(\mathcal{P})$ et $(\mathcal{Q})$ sont orthogonaux si et seulement si: $~\vec{u} \cdot \vec{n}=0$
مثال
Montrer que les plans $(\mathcal{P})$ et $(\mathcal{Q})$ sont orthogonaux tels que :$\\[0.2cm]$ $(\mathcal{P}) : x-y+z+1=0 \quad \quad$ et $ \quad \quad (\mathcal{Q}) : 2x+y-z-5=0 \\[0.3cm]$ On a $~~\vec{n}_P(1 ; -1 ; 1) \quad $ et $\quad \vec{n}_Q (2 ; 1 ; -1) \\[0.2cm]$ $\vec{n}_P ~$ et $~ \vec{n}_Q~$ sont 2 vecteurs normaux respectivement à $(\mathcal{P})$ et $(\mathcal{Q}) \\[0.2cm]$ On a $~\vec{n}_P \cdot \vec{n}_Q =1 \cdot 2- 1 \cdot 1 -1 \cdot 1 =0\\[0.2cm]$ Donc $~\vec{n}_P \perp \vec{n}_Q \\[0.2cm]$ D'où $(\mathcal{P})$ et $(\mathcal{Q})$ sont orthogonaux
Distance d'un point à un plan
تعريف
Soit $(\mathcal{P}) : ~ax+by+cz+d=0 ~$ un plan et $~A(x_A ; y_A ; z_A )~$ un point de l'espace $\\[0.2cm]$ La distance du point $A$ au plan $(\mathcal{P})$ est $~d(a ; (\mathcal{P})) =\frac{|ax_A +by_A+cz_A+d|}{\sqrt{a^2 +b^2 +c^2}}$
تطبيق
Calculer la distance de $A(1 ; 2 ; 1)$ au plan $~(\mathcal{P}) : ~x-y+z+1=0 \\[0.3cm]$ $~d(a ; (\mathcal{P})) =\frac{|1-2+1+1|}{\sqrt{1+1+1}} = \frac{1}{\sqrt{3}}= \frac{\sqrt{3}}{3} $
Etude analytique de la sphère
لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو
- ملخصات الدروس غير محدودة
- فيديو مجاني في كل درس
- تمرين مصحح مجاني
- اختبار تفاعلي
Signaler une erreur