Mouvements plans

Lancer d’un projectile

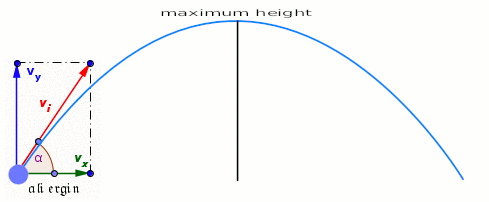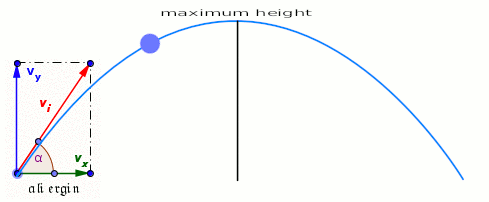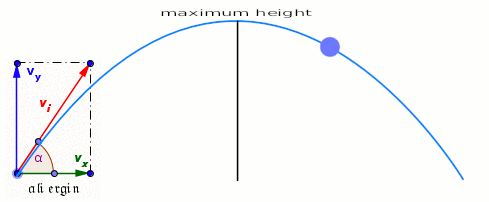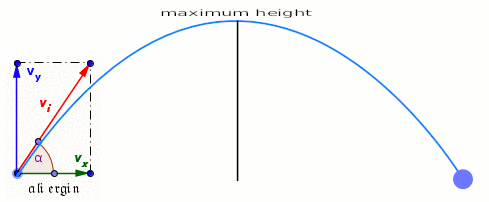
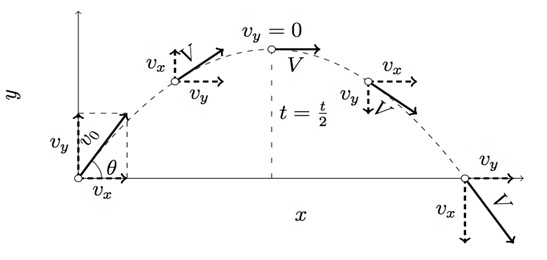
Un projectile est lancé à l’instant t = 0 avec une vitesse $$\overrightarrow{V_{0}}$$ faisant un angle $$\alpha$$ par rapport à l’horizontale.
On assimile le projectile à un point matériel ce qui nous permet de le réduire au mouvement de son centre d’inertie M.
L’étude est réalisée avec les approximations suivantes :
On considère que le champ de pesanteur g est uniforme.
On néglige la poussée d’Archimède et les frottements par rapport au poids du système.
On étudie le mouvement du projectile dans le référentiel terrestre qu’on suppose galiléen avec une bonne approximation, muni d’un repère cartésien (Oxyz).
Le mouvement a lieu dans le plan (Oxy) qui contient les vecteurs $$\overrightarrow{V_{0}} \text { et } \vec{g}$$

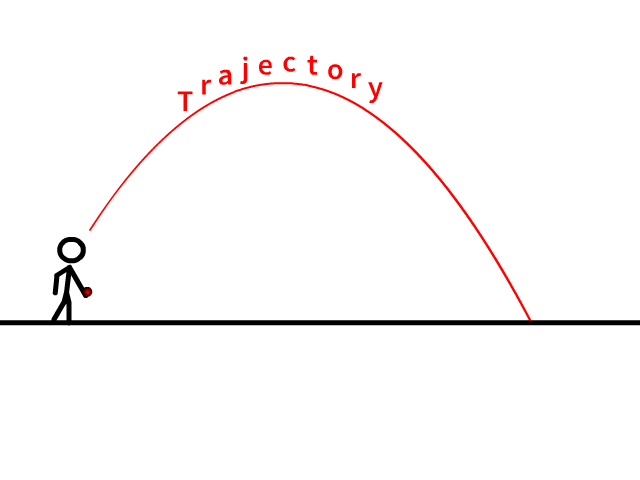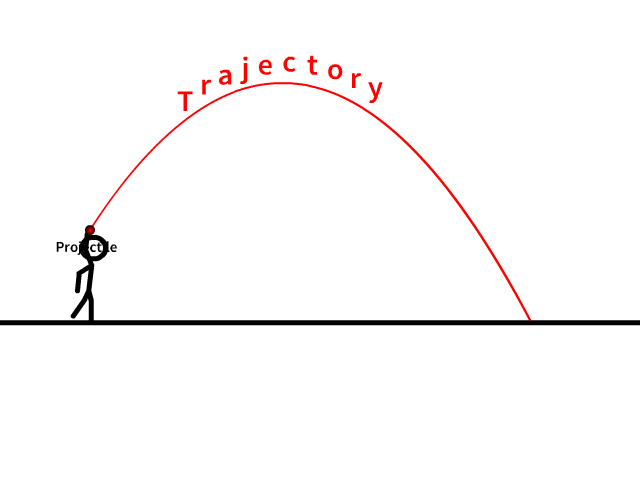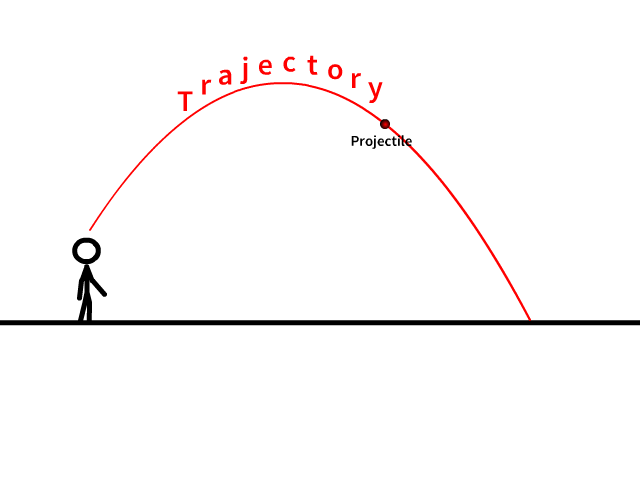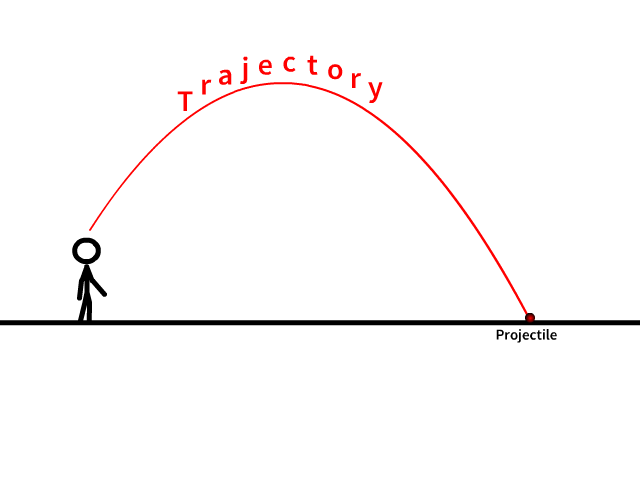
Etude du mouvement

Système étudié

Le projectile qui peut être un ballon ou une bille ou n’importe quel objet

Bilan des forces

$$\vec{P}$$ : Le poids du projectile

La deuxième loi de newton

Dans une repère terrestre supposé galiléen, on applique la 2ème loi de newton
$$\vec{P}=m \vec{a}$$
$$m \vec{g}=m \vec{a}$$
$$\vec{a}=\vec{g}$$

En projetant sur les axes (ox), (oy) et (oz) on obtient :
$$\left\{\begin{array}{c}a_{x}=0 \\a_{y}=-g \\a_{z}=0\end{array}\right.$$

Les équations horaires de la vitesse

On a :
$$\left\{\begin{array}{c}a_{x}=0 \\a_{y}=-g \\a_{z}=0\end{array}\right.$$
Alors
$$\left\{\begin{array}{l}\frac{d V_{x}}{d t}=0 \\\frac{d V_{y}}{d t}=-g \\\frac{d V_{z}}{d t}=0\end{array}\right.$$

Par intégration, on obtient :
$$\left\{\begin{array}{c}V_{x}(t)=V_{0 x}=V_{0} \cos \alpha \\V_{y}(t)=-g t+V_{0 y}=-g t+V_{0} \sin \alpha \\V_{z}(t)=V_{0 z}=0\end{array}\right.$$

Équations horaires du mouvement

On a les équations horaires de la vitesse :
$$\left\{\begin{array}{c}V_{x}(t)=V_{0 x}=V_{0} \cos \alpha \\V_{y}(t)=-g t+V_{0 y}=-g t+V_{0} \sin \alpha \\V_{z}(t)=V_{0 z}=0\end{array}\right.$$
Alors
$$\left\{\begin{array}{c}\frac{d x}{d t}=V_{0} \cos \alpha \\\frac{d y}{d t}=-g t+V_{0} \sin \alpha \\\frac{d z}{d t}=0\end{array}\right.$$
Pa intégration, on obtient :
$$\left\{\begin{array}{c}x(t)=V_{0} \cos \alpha t+X_{0} \\y(t)=-\frac{1}{2} g t^{2}+V_{0} \sin \alpha t+Y_{0} \\z(t)=Z_{0}\end{array}\right.$$
En revenant aux conditions initiales, on peut dire que :
$$X_{0}=Y_{0}=Z_{0}=0$$
Alors
$$x(t)=V_{0} \cos \alpha t$$
$$y(t)=-\frac{1}{2} g t^{2}+V_{0} \sin \alpha t$$
$$z(t)=0$$
Les équations horaires nous aide à trouver les coordonnées x,y et z dans n’importe quel moment de la trajectoire

Équation de la trajectoire et les caractéristiques de la trajectoire

L’équation de la trajectoire est une équation qui donne la relation entre la coordonnée x et la coordonnée y, pour obtenir l’équation de la trajectoire, on trouve t en fonction de x et puis après on remplace t par son expréssion dans l’équation de y.

On a $$x(t)=V_{0} \cos \alpha t$$
Alors $$t=\frac{x}{V_{0} \cos \alpha}$$
On remplace l’expréssion de t sur $$y(t)=-\frac{1}{2} g t^{2}+V_{0} \sin \alpha t$$
$$y=-\frac{1}{2} g\left(\frac{x}{V_{0} \cos \alpha}\right)^{2}+V_{0} \sin \alpha\left(\frac{x}{V_{0} \cos \alpha}\right)$$
$$y=-\frac{1}{2} g\left(\frac{x^{2}}{V_{0}^{2} \cos ^{2} \alpha}\right)+V_{0} \sin \alpha\left(\frac{x}{V_{0} \cos \alpha}\right)$$
$$y=-\frac{1}{2} \frac{g}{V_{0}{ }^{2} \cos ^{2} \alpha} \cdot x^{2}+\tan \alpha \cdot x$$

Les coordonnées du sommet

Parmi les coordonnées les plus demandées on peut citer les coordonnées du sommet
Dans le sommet, on sait que $$V_{y}=0$$

Alors l’équation $$V_{y}(t)=-g t+V_{0} \sin \alpha$$ devient
$$g t_{\text {sommet }}=V_{0} \sin \alpha$$
$$t_{\text {sommet }}=\frac{V_{0} \sin \alpha}{g}$$
Et après on remplace t_{sommet} par sa valeur dans les deux équations horaires de x et y
$$x_{\text {sommet }}=V_{0} \cos \alpha t_{\text {sommet }}$$
$$y_{\text {sommet }}=-\frac{1}{2} g t_{\text {sommet }}{ }^{2}+V_{0} \sin \alpha t_{\text {sommet }}$$

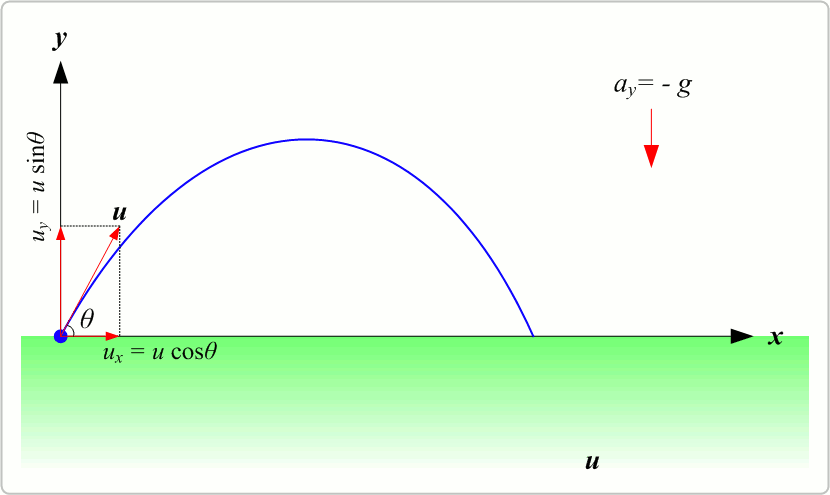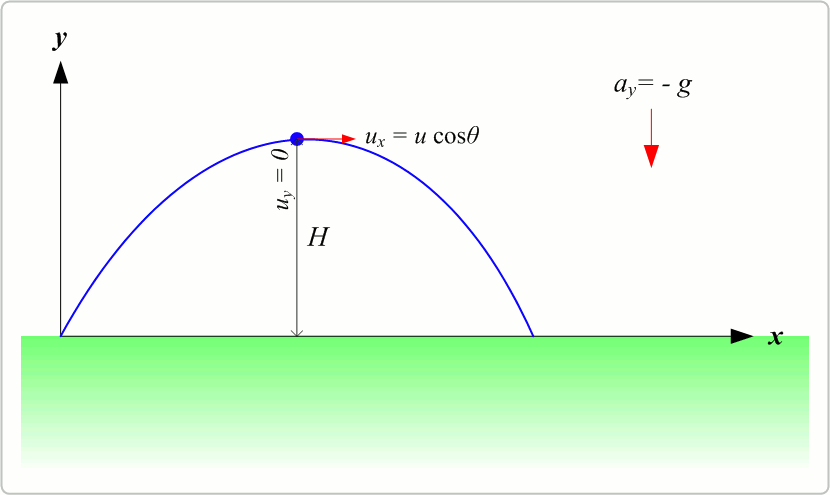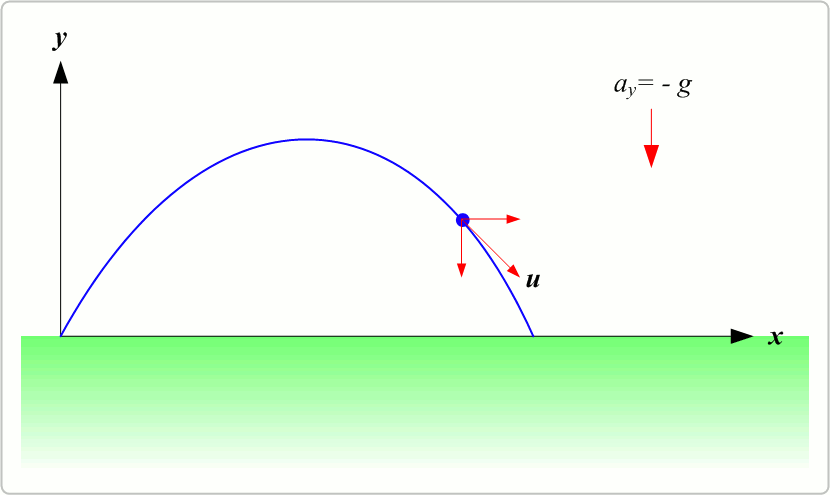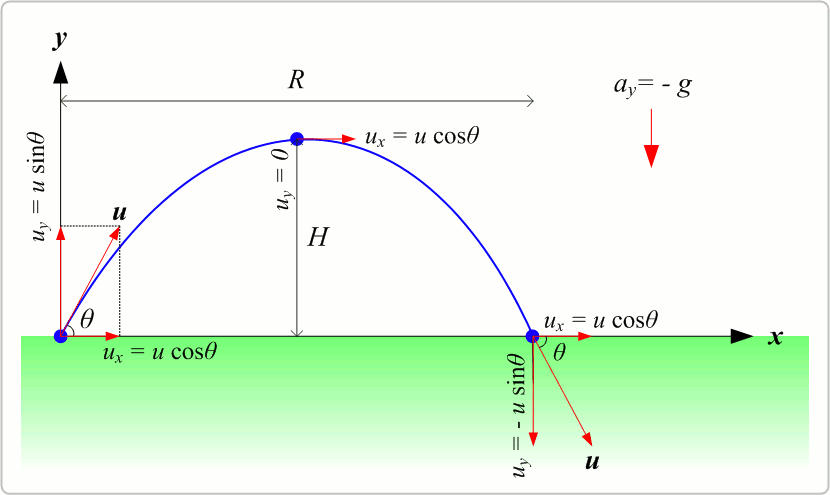
La distance parcourue par le projectile sur l'axe horizontal

Pour déterminer la distance parcourue par le projectile sur l’axe horizontal, on sait que vers la fin de la trajectoire la cordonnée de y est nulle
En utilisant l’équation de la trajectoire
$$y=-\frac{1}{2} \frac{g}{V_{0}^{2} \cos ^{2} \alpha} \cdot x^{2}+\tan \alpha \cdot x$$
$$0=-\frac{1}{2} \frac{g}{V_{0}^{2} \cos ^{2} \alpha} \cdot x^{2}+\tan \alpha \cdot x$$
Et on résout l’équation du deuxième degré pour trouver la distance parcourue par le projectile sur l’axe horizontal

لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

النسخة المجانية لكيزاكو:

• ملخصات الدروس غير محدودة
• فيديو مجاني في كل درس
• تمرين مصحح مجاني
• اختبار تفاعلي

إنشاء حساب مجاني