Notions générales sur le mouvement
Le mouvement d’un corps est relatif au référentiel choisi, c’est-à-dire que les corps ne se déplacent que par rapport à d’autres corps, donc pour décrire le mouvement d’un corps on doit choisir un solide de référence fixe appelé référentiel.
Pour que la description du mouvement d’un système soit précise, il faut indiquer sa position et l’instant ou la date à laquelle il occupe cette position, donc nous avons besoin de deux repères : Repère d’espace par rapport auquel on repère les positions du système et repère de temps c’est–à-dire d’une horloge permettant un repérage des dates
Référentiel
L’étude du mouvement d’un système nécessite l’étude du mouvement de tous ses points, mais on peut étudier uniquement le mouvement de son centre d’inertie G, car il nous donne le mouvement global du système
Vecteur position
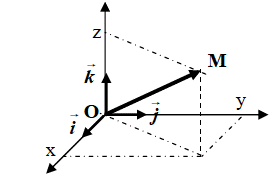
Le vecteur $$\overrightarrow{O M}$$ définit, à chaque instant , la position du mobile dans le repère $$R_{o}$$.
Expression en coordonnées cartésiennes $$(x, y, z)$$
Le vecteur position s'écrit $$\overrightarrow{O M}=x \vec{i}+y \vec{j}+z \vec{k}$$ où $$(x, y, z)$$ sont les coordonnées cartésiennes du point dans le repère $$R_{0}$$.
$$O M=\sqrt{x^{2}+y^{2}+z^{2}}$$ est le module du vecteur position, c'est une grandeur scalaire (nombre) positive qui représente la distance (en m) entre O et M.
Les principaux référentiels
Référentiel terrestre

تعريف
Le Référentiel terrestre est constitué d’un point du sol et de trois axes, en général un axe vertical et deux axes dans le plan horizontal, on l’utilise pour étudier le mouvement d’objets se déplaçant à la surface ou près de la surface de la terre
مثال
Le déplacement d’une voiture, la chute d’un objet, un jet d’un projectile.
Référentiel géocentrique
تعريف
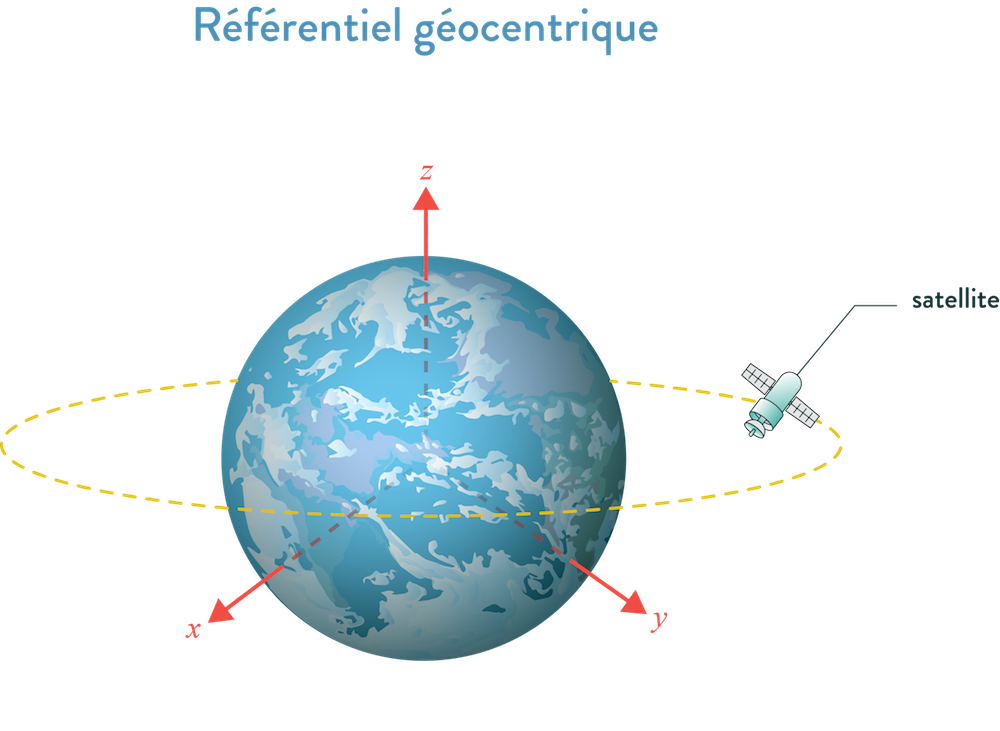
Le référentiel géocentrique est un référentiel dont l’origine est le centre de la terre et dont les trois axes pointent vers des étoiles suffisamment lointaines qui apparaissent fixes, on l’utilise pour étudier le mouvement d’objets se déplaçant autour de la Terre, pour lesquels la rotation de la terre ne peut pas être négligé.
مثال
La lune, les satellites artificielles.
Référentiel héliocentrique
تعريف
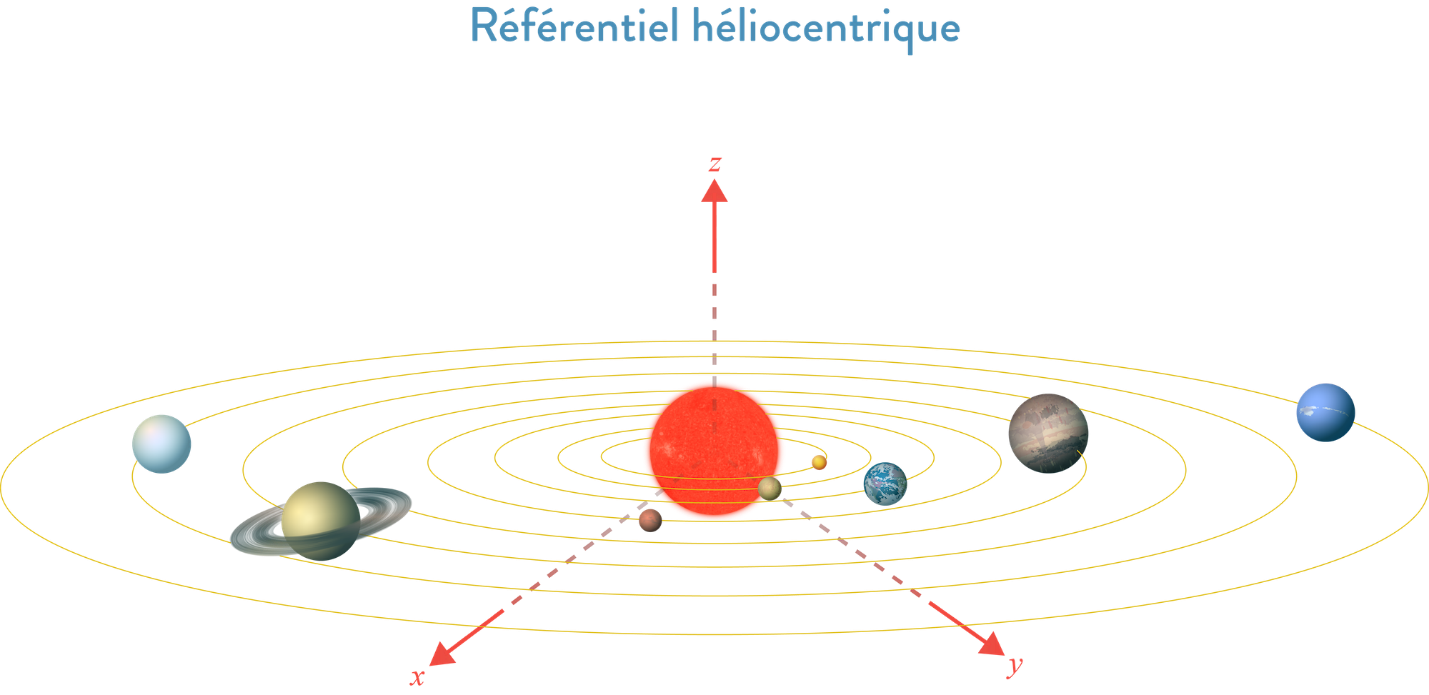
Le référentiel héliocentrique est un référentiel dont l’origine est le centre du soleil et dont les trois axes pointent vers des étoiles suffisamment lointaines qui apparaissent fixes, on l’utilise pour étudier le mouvement d’objets se déplaçant autour du soleil.
مثال
Les planètes, les comètes, les astéroïdes.
Vecteur vitesse
تعريف
Dans un référentiel donné, le vecteur vitesse instantanée du centre d’inertie G d’un solide à un instant t est la dérivée par rapport au temps du vecteur position à cet instant : $$\overrightarrow{v_{\mathrm{G}}(\mathrm{t})}=\frac{\mathrm{d} \overrightarrow{\mathrm{OG}}}{\mathrm{dt}}$$
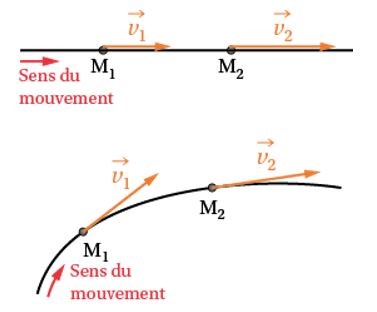
Le vecteur vitesse d’un point mobile est toujours tangent à la trajectoire et dirigé dans le sens du mouvement.
L’expression du vecteur vitesse instantanée dans un repère cartésien est :
On a $$\overrightarrow{v_{\mathrm{G}}(\mathrm{t})}=\frac{\mathrm{d} \overrightarrow{\mathrm{OG}}}{\mathrm{dt}}$$ et $$\overrightarrow{\mathrm{OG}}(\mathrm{t})=\mathrm{x}(\mathrm{t}) \overrightarrow{\mathrm{\imath}}+\mathrm{y}(\mathrm{t}) \overrightarrow{\mathrm{j}}+\mathrm{z}(\mathrm{t}) \overrightarrow{\mathrm{k}}$$
Alors $$\overrightarrow{v_{\mathrm{G}}(\mathrm{t})}=\frac{\mathrm{d}}{\mathrm{dt}}(\mathrm{x}(\mathrm{t}) \overrightarrow{1}+\mathrm{y}(\mathrm{t}) \vec{\jmath}+\mathrm{z}(\mathrm{t}) \overrightarrow{\mathrm{k}})$$
$$\text { Donc } \overrightarrow{v_{\mathrm{G}}(\mathrm{t})}=\frac{\mathrm{dx}(\mathrm{t})}{\mathrm{dt}} \overrightarrow{\mathrm{l}}+\frac{\mathrm{dy}(\mathrm{t})}{\mathrm{dt}} \overrightarrow{\mathrm{\jmath}}+\frac{\mathrm{d} z(\mathrm{t})}{\mathrm{dt}} \overrightarrow{\mathrm{k}} \text { alors, } \overrightarrow{v_{\mathrm{G}}(\mathrm{t})}=\mathrm{v}_{\mathrm{x}}(\mathrm{t}) \overrightarrow{\mathrm{i}}+\mathrm{v}_{\mathrm{y}}(\mathrm{t}) \overrightarrow{\mathrm{\jmath}}+\mathrm{v}_{\mathrm{z}}(\mathrm{t}) \overrightarrow{\mathrm{k}}$$
Avec $$\mathrm{v}_{\mathrm{x}}(\mathrm{t}), \mathrm{v}_{\mathrm{y}}(\mathrm{t}) \text { et } \mathrm{v}_{\mathrm{z}}(\mathrm{t})$$ sont les coordonnées cartésiennes du vecteur vitesse
Vecteur accélération
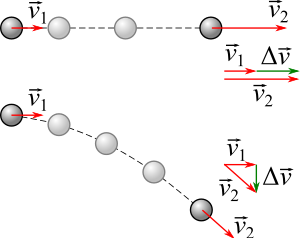
Dans un référentiel donné, le vecteur accélération du centre d’inertie G d’un solide, à instant t, est la dérivée par rapport au temps du vecteur vitesse : $$\mathrm{a}_{\mathrm{G}}(\mathrm{t})=\frac{\mathrm{d} \overrightarrow{\mathrm{V}_{\mathrm{G}}}}{\mathrm{d} \mathrm{t}}$$ son unité dans le (S.I) est $$\text { m.s }^{-2}$$
L’accélération désigne le taux de variation de la vitesse d'un objet en mouvement c’est –à-dire la variation de la vitesse pendant une certaine durée : donc $$\mathrm{a}=\frac{\mathrm{d} v}{\mathrm{dt}}$$
Si un objet maintient une vitesse constante v = Cte, alors a = 0, il n'y a pas d'accélération, donc L'accélération se produit lorsque la vitesse de l'objet varie.
Si v augmente alors $$\frac{\mathrm{d} v}{\mathrm{dt}}>0, \text { donc } \mathrm{a}>0$$
Si v diminue alors $$\frac{\mathrm{d} v}{\mathrm{dt}}<0, \text { donc } \mathrm{a}<0$$
Expression du vecteur accélération dans un repère cartésien
On a $$\overrightarrow{\mathrm{a}_{\mathrm{G}}}(\mathrm{t})=\mathrm{a}_{\mathrm{x}}(\mathrm{t}) \overrightarrow{\mathrm{i}}+\mathrm{a}_{\mathrm{y}}(\mathrm{t}) \vec{\jmath}+\mathrm{a}_{\mathrm{z}}(\mathrm{t}) \overrightarrow{\mathrm{k}} \text { avec } \mathrm{a}_{\mathrm{x}}(\mathrm{t}), \mathrm{a}_{\mathrm{y}}(\mathrm{t}) \text { et } \mathrm{a}_{\mathrm{z}}(\mathrm{t})$$ sont les coordonnées cartésiennes du vecteur vitesse, Avec :
$$\mathrm{a}_{\mathrm{x}}(\mathrm{t})=\frac{\mathrm{dv}_{\mathrm{x}}(\mathrm{t})}{\mathrm{d} \mathrm{t}}=\frac{\mathrm{d}^{2} \mathrm{x}(\mathrm{t})}{\mathrm{dt}^{2}}$$
$$\mathrm{a}_{\mathrm{y}}(\mathrm{t})=\frac{\mathrm{dv}_{\mathrm{y}}(\mathrm{t})}{\mathrm{dt}}=\frac{\mathrm{d}^{2} \mathrm{y}(\mathrm{t})}{\mathrm{dt}^{2}}$$
$$\mathrm{a}_{\mathrm{z}}(\mathrm{t})=\frac{\mathrm{dv}_{\mathrm{z}}(\mathrm{t})}{\mathrm{d} \mathrm{t}}=\frac{\mathrm{d}^{2} \mathrm{z}(\mathrm{t})}{\mathrm{dt}^{2}}$$
Expression du vecteur accélération dans un repère de Frenet
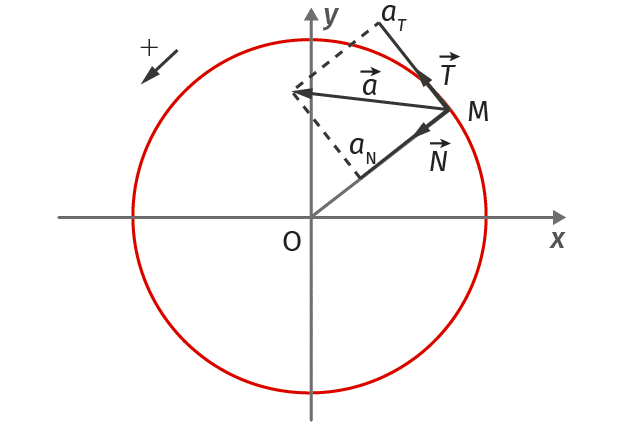
Le repère Frenet est un repère mobile orthonormé lié au mobile M, son origine est confondu avec le point M, son vecteur unitaire $$\overrightarrow{\mathrm{u}}$$ est tangent à la trajectoire et dirigé dans le sens du mouvement alors que le vecteur unitaire $$\overrightarrow{\mathrm{n}}$$ est perpendiculaire à $$\overrightarrow{\mathrm{u}}$$ et dirigé vers l’intérieur de la concavité de la trajectoire. L’expression du vecteur vitesse dans un repère de Frenet est : $$a_{G}(t)=a_{T} \vec{u}+a_{N} \vec{n}$$ Avec $$\mathrm{a}_{\mathrm{T}}=\frac{\mathrm{d} \mathrm{v}_{\mathrm{G}}}{\mathrm{d} \mathrm{t}}$$ est l’accélération tangentielle $$\mathrm{a}_{\mathrm{N}}=\frac{\mathrm{v}_{\mathrm{G}}^{2}}{\rho}$$ est l’accélération normale tel que \rho\ : c’est le rayon de courbure de la trajectoire du mobile M Nature du mouvement Si $$\frac{\mathrm{dv}_{\mathrm{G}}}{\mathrm{dt}}>0$$ : alors la vitesse augmente, donc le mouvement est accéléré
Si $$\frac{\mathrm{dv}_{\mathrm{G}}}{\mathrm{dt}}=0$$ : alors la vitesse reste constante, donc le mouvement est uniforme
Si $$\frac{\mathrm{dv}_{\mathrm{G}}}{\mathrm{dt}}<0$$ : alors la vitesse diminue, donc le mouvement est retardé
Lois de Newton
لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

- ملخصات الدروس غير محدودة
- فيديو مجاني في كل درس
- تمرين مصحح مجاني
- اختبار تفاعلي