Les limites 1BAC

Fiche de cours

Le concept de limite est une partie importante du fondement de l'analyse mathématique. Ne pas le maîtriser entraînera des problèmes lorsque nous discuterons des concepts de convergence, de continuité et de dérivée dans les prochains chapitres. Si les élèves comprennent le concept de limites, les concepts connexes deviendront plus faciles à utiliser.

Historiquement, les principes de base du calcul ont été introduits à l'aide de deux problèmes : le problème de la tangente et le problème de l'aire. Comme nous le verrons dans ce chapitre et les chapitres suivants, les solutions à ces deux problèmes font appel à la notion de limites.

Vidéo Introduction aux limites

15 min

Voir la vidéo

Limite à l’infini

Limite finie en +∞ , en -∞

Activité

Considérons la fonction :

$\begin{aligned} f: \mathbb{R} \backslash\{1\} &\rightarrow \mathbb{R} \\ x &\rightarrow\frac{2 x}{x-1}\end{aligned}$

La courbe représentative de $f$ :

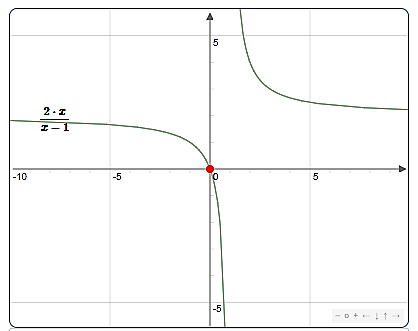
A partir de la courbe et du tableau, lorsque x prend des valeurs de plus en plus grandes positives, c'est-à-dire lorsque $x$ tend vers $+\infty, f(x)$ tend vers $2 .$ On dit que la limite de $f(x)$ est $2$ quand $x$ tend vers $+\infty\\[0.2cm]$ et on écrit $\lim\limits _{x \rightarrow+\infty} f(x)=2\\[0.2cm]$
A partir de la courbe et du tableau, lorsque $x$ est négatif et s'éloigne de plus en plus de $0$ , c'est-à-dire lorsque $x$ tend vers $-\infty, f(x)$ tend vers $2 .$ On dit que la limite de $f(x)$ est $2$ quand $x$ tend vers $-\infty\\[0.2cm]$ et on écrit $\lim\limits _{x \rightarrow-\infty} f(x)=2$.

تعريف

Soit $f$ une fonction définie sur un intervalle de la forme $] a,+\infty[$ avec $a$ un réel quelconque .On dit que la fonction $f$ tend vers $l$ quand $x$ tend vers $+\infty$ si : $\\[0.2cm]$ $(\forall \varepsilon>0)(\exists B>0)\left(\forall x \in D_{f}\right)(x>B \Rightarrow|f(x)-l|<\varepsilon) .\\[0.2cm]$ Et on écrit : $\lim\limits _{x \rightarrow+\infty} f(x)=l \\[0.2cm]$
Soit $f$ une fonction définie sur un intervalle de la forme $]-\infty, a[$ avec $a$ un réel quelconque .On dit que la fonction $f$ tend vers $l$ quand $x$ tend vers $-\infty$ si : $\\[0.2cm]$ $(\forall \varepsilon>0)(\exists B>0)\left(\forall x \in D_{f}\right)(x<-B \Rightarrow|f(x)-l|<\varepsilon). \\[0.2cm]$ Et on écrit: $\lim\limits _{x \rightarrow-\infty} f(x)=l$

ما يجب معرفته

L’interprétation géométrique

- $\lim\limits _{x \rightarrow+\infty} f(x)=l$,la courbe de la fonction se rapproche de plus en plus de la droite d'équation $y=l$ quand $x$ tend vers $+\infty$.

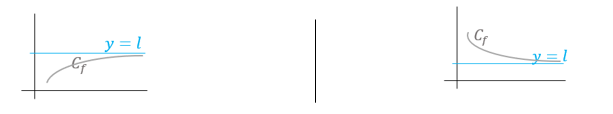
- $\lim\limits _{x \rightarrow-\infty} f(x)=l$, la courbe de la fonction se rapproche de plus en plus de la droite d'équation $y=l$ quand $x$ tend vers $-\infty$.

-Et alors on dit que la droite $y=l$ est une asymptote horizontale.

انتباه

- Si $f$ est paire : $\lim\limits _{x \rightarrow-\infty} f(x)=\lim\limits _{x \rightarrow+\infty} f(x)\\[0.2cm]$ - Si $f$ est impaire : $\lim\limits _{x \rightarrow-\infty} f(x)=-\lim\limits _{x \rightarrow+\infty} f(x)$

ما يجب معرفته

La position de la courbe par rapport à l’asymptote horizontale

Cette position se détermine par le signe de $f(x)-l$.

1- Si $f(x)-l \geq 0$, alors $C_{f}$ est au-dessus de l'asymptote.

2- Si $f(x)-l \leq 0$, alors $C_{f}$ est au-dessous de l'asymptote.

Remarque

Cas des fonctions usuelles

Les fonctions :

$x \longmapsto \frac{k}{|x|}~ ;~ x \longmapsto \frac{k}{\sqrt{|x|}}~ ; ~x \longmapsto \frac{k}{|x|^{n}} ~; ~\forall(k, n) \in \mathbb{R} \times \mathbb{N}^{*}$

Toutes les courbes représentatives de ces fonctions admettent l’axe des abscisses comme asymptote.

مثال

Soit:$f(x)=\frac{1}{x^{2}+1}$

Déterminons $\lim\limits _{x \rightarrow+\infty} f(x)$ et $\lim\limits _{x \rightarrow-\infty} f(x):$

$\forall x \in \mathbb{R}^{*}:$ On a $x^{2}+1 \geq x^{2}$

Alors $:|f(x)| \leq \frac{1}{x^{2}}$ et on a $\lim\limits _{x \rightarrow+\infty} \frac{1}{x^{2}}=\lim\limits _{x \rightarrow-\infty} \frac{1}{x^{2}}=0$

Donc: $\lim\limits _{x \rightarrow+\infty} f(x)=\lim\limits _{x \rightarrow-\infty} f(x)=0$

Soit: $f(x)=\frac{-5 x^{2}+1}{x^{2}}$

Montrons que $\lim\limits _{x \rightarrow-\infty} f(x)=-5$ :

$\lim\limits _{x \rightarrow-\infty} f(x)-(-5)=\lim\limits _{x \rightarrow-\infty} \frac{-5 x^{2}+1+5 x^{2}}{x^{2}}=\lim\limits _{x \rightarrow-\infty} \frac{1}{x^{2}}=0$

Donc: $\lim\limits _{x \rightarrow-\infty} f(x)=-5$

Limite infinie en +∞ , en -∞

Activité

Considérons la fonction $f: \mathbb{R} \rightarrow \mathbb{R}$ $x \mapsto x^{3}$ La courbe représentative de $f$ :

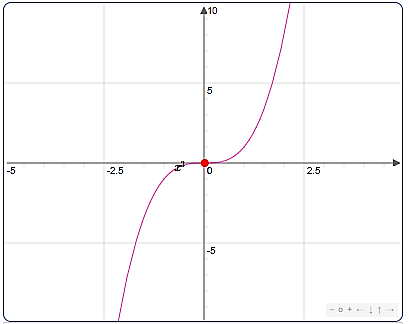
A partir de la courbe et du tableau, lorsque $x$ prend des valeurs de plus en plus grandes positives, c'est-à-dire lorsque $x$ tend vers $+\infty, f(x)$ tend vers $+\infty.\\[0.2cm]$ On dit que la limite de $f(x)$ est $+\infty$ quand $x$ tend vers $+\infty\\[0.2cm]$ et on écrit $~\lim\limits _{x \rightarrow+\infty} f(x)=+\infty \\[0.2cm]$
A partir de la courbe et du tableau, lorsque $x$ est négatif et s'éloigne de plus en plus de $0$ , c'est-à-dire lorsque $x$ tend vers $-\infty, f(x)$ tend vers $-\infty.\\[0.2cm]$ On dit que la limite de $f(x)$ est $-\infty$ quand $x$ tend vers $-\infty\\[0.2cm]$ et on écrit $\lim\limits _{x \rightarrow-\infty} f(x)=-\infty .$

تعريف

Soit $f$ une fonction définie sur intervalle de la forme $] a,+\infty[$ où $a$ un réel quelconque. On dit que la fonction $f$ tend vers $+\infty$ quand $x$ tend vers $+\infty$ si : $\\[0.2cm](\forall A>0)(\exists B>0)\left(\forall x \in D_{f}\right)~(x>B \Rightarrow f(x)>A) .\\[0.2cm]$ Et on écrit : $\lim\limits _{x \rightarrow+\infty} f(x)=+\infty\\[0.2cm]$
$\lim\limits _{x \rightarrow+\infty} f(x)=-\infty ~~$ si :$\\[0.2cm](\forall A>0)(\exists B>0)\left(\forall x \in D_{f}\right)(x>B \Rightarrow f(x)<-A)\\[0.2cm]$
$\lim\limits _{x \rightarrow-\infty} f(x)=-\infty~~ $ si :$\\[0.2cm](\forall A>0)(\exists B>0)\left(\forall x \in D_{f}\right)(x<-B \Rightarrow f(x)<-A)\\[0.2cm]$
$\lim\limits _{x \rightarrow-\infty} f(x)=+\infty~~$ si : $\\[0.2cm](\forall A>0)(\exists B>0)\left(\forall x \in D_{f}\right)(x<-B \Rightarrow f(x)>A)$.

Remarque

Cas des fonctions usuelles

Soit $~ n \in \mathbb{N}^{*} :\quad $ $\lim\limits _{x \rightarrow+\infty} x^{n}=+\infty \\[0.2cm]$ si $n$ est paire : $\quad \lim\limits _{x \rightarrow-\infty} x^{n}=-\infty \\[0.2cm]$ si $n$ est impaire : $\quad \lim\limits _{x \rightarrow+\infty} \sqrt{x}=+\infty $

Vidéo Limites à l'infini

15 min

Voir la vidéo

Limite en un réel a

Activité

Considérons les fonctions $ f: \left\{\begin{array}{lcl}\mathbb{R} \rightarrow \mathbb{R} \\ x \rightarrow x^{3} \end{array}\right.~$ et $~ g: \left\{\begin{array}{lcl}\mathbb{R} \rightarrow \mathbb{R} \\ x \rightarrow \frac{1}{x} \end{array}\right.$

A partir du tableau, lorsque $x$ se rapproche de $0$ , c'est-à-dire lorsque $x$ tend vers $0$ , $f(x)$ tend vers $0 .$ On dit que la limite de $f(x)$ est 0 quand $x$ tend vers 0 et on écrit $\lim\limits _{x \rightarrow 0} f(x)=0$

A partir du tableau, lorsque $x$ se rapproche de 0, c'est-à-dire lorsque $x$ tend vers 0, $g(x)$ tend vers $+\infty$. On dit que la limite de $g(x)$ est $+\infty$ quand $x$ tend vers $0$ et on écrit $\lim\limits _{x \rightarrow 0} g(x)=+\infty$.

تعريف

Soit $f$ une fonction définie sur un intervalle de la forme $] a-r, a+r[$ ou un intervalle de la forme $] a-r, a+r\left[-\{r\}\right.$ tel que $r \in \mathbb{R}^{+*} .$

$f$ tend vers $l$ quand $x$ tend vers $a$ si :

$(\forall \varepsilon>0)(\exists \alpha>0)\left(\forall x \in D_{f}\right)(0<|x-a|<\alpha \Rightarrow|f(x)-l|<\varepsilon)$

et on écrit $\lim\limits _{x \rightarrow a} f(x)=l$

خاصية

Si $ f $ admet une limite $~l~$ en $a$ alors cette limite est unique.

Remarque

$\lim\limits _{x \rightarrow a}|f(x)|=l \Leftrightarrow \lim\limits _{x \rightarrow a} f(x)=l$ ou $\lim\limits _{x \rightarrow a} f(x)=-l$
Cas des fonctions usuelles:

Soit $n \in \mathbb{N}^{*}: \quad \lim\limits _{x \rightarrow 0} x^{n}=0$

مثال

$\lim\limits _{x \rightarrow 0} x=0 ;$

$\lim\limits _{x \rightarrow 0} x^{4}=0$

Limite à droite , limite à gauche

Activité

Considérons la fonction $f: \left\{\begin{array}{lcl}\mathbb{R} \backslash \{2\} \rightarrow \mathbb{R} \\ \chi \rightarrow \frac{|x-2| x}{x-2}\end{array}\right. $

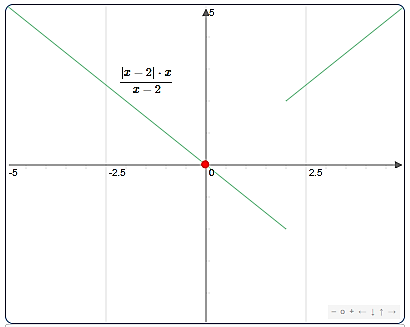
A partir de la courbe et du tableau, lorsque $x$ se rapproche de $2$ sur la droite, $f(x)$ se rapproche de $2 \\[0.2cm]$ On dit que la limite de $f(x)$ est 2 quand $x$ tend vers $2$ à droite et on écrit $\lim\limits _{\substack{x \rightarrow 2 \\ x>2}} f(x)=2\\[0.2cm]$
A partir de la courbe et du tableau, lorsque $x$ se rapproche de $2$ sur la gauche, $f(x)$ se rapproche de $-2\\[0.2cm]$ On dit que la limite de $f(x)$ est $-2$ quand $x$ tend vers $2$ à gauche et on écrit $\lim\limits _{\substack{x \rightarrow 2 \\ \rightarrow x<2}} f(x)=-2$.

تعريف

Soit $f$ une fonction définie sur un intervalle de la forme $] a, a+r\left[\right.$ tel que $r \in \mathbb{R}^{+*} .\\[0.2cm]$ $f$ tend vers $l$ quand $x$ tend vers $a$ à droite si la proposition suivante est vraie: $\\[0.2cm]$ $(\forall \varepsilon>0)(\exists \alpha>0)\left(\forall x \in D_{f}\right)(a<x<a+\alpha \Rightarrow|f(x)-l|<\varepsilon) \\[0.2cm] $ Et on écrit $~\lim\limits _{x \rightarrow a} f(x)=l~$ ou $~\lim\limits _{x \rightarrow a^{+}} f(x)=l\\[0.2cm]$
Soit $f$ une fonction définie sur un intervalle de la forme $] a-r, a\left[\right.$ tel que $r \in \mathbb{R}^{+*} .\\[0.2cm]$ $f$ tend vers $l$ quand $x$ tend vers $a$ à gauche si la proposition suivante est vraie :$\\[0.2cm](\forall \varepsilon>0)(\exists \alpha>0)\left(\forall x \in D_{f}\right)(a-\alpha<x<a \Rightarrow|f(x)-l|<\varepsilon)\\[0.2cm]$ E on écrit $~\lim\limits _{x \rightarrow a} f(x)=l~$ ou $~\lim\limits _{x \rightarrow a^{-}} f(x)=l$

نظرية

Une fonction $f$ admet une limite $l$ en $a$ si et seulement si elle admet une limite à droite de $a$ égale à sa limite à gauche de $a$ égale à $l\\[0.2cm]$ $\lim\limits _{x \rightarrow a} f(x)=l \Leftrightarrow \lim\limits _{x \rightarrow a^{+}} f(x)=l~$ et $~\lim\limits _{x \rightarrow a^{-}} f(x)=l$

مثال

Soit la fonction $f: x \mapsto \frac{(x+5)^{2}}{\left|x^{2}-5\right|}$ :

Pour étudier la limite de $f$ en $a=-5$, déterminons $\lim\limits _{x \rightarrow-5^{+}} f(x)$ et $\lim\limits _{x \rightarrow-5^{-}} f(x)=l$

$\forall x \in \mathbb{R} \backslash\{5,-5\}:$

Si $-5<x<5: f(x)=\frac{(x+5)^{2}}{|x+5||x-5|}=-\frac{x+5}{x-5}$

Donc: $\lim\limits _{x \rightarrow-5^{+}} f(x)=\lim\limits _{x \rightarrow-5^{+}}-\frac{x+5}{x-5}=0$

Si $x<-5: f(x)=\frac{(x+5)^{2}}{|x+5||x-5|}=\frac{x+5}{x-5}$

Donc: $\lim\limits _{x \rightarrow-5^{-}} f(x)=\lim\limits _{x \rightarrow-5^{-}} \frac{x+5}{x-5}=0$

Finalement $\lim\limits _{x \rightarrow-5^{-}} f(x)=\lim\limits _{x \rightarrow-5^{+}} f(x)=0$

et on en déduit $\lim\limits _{x \rightarrow-5} f(x)=0$

Remarque

Interprétation géométrique