Ondes mécaniques progressives périodiques 2BAC

Fiche de cours

Les ondes progressives périodiques

Les phénomènes périodiques

Un phénomène périodique est un phénomène qui se répète identiquement à lui-même à des Intervalles de temps réguliers.

مثال

Rotation de la terre autour d'elle-même
Mouvement de la Terre autour du soleil

Exemples d'ondes mécaniques progressives périodiques

Ondes à la surface de l'eau

L'onde mécanique circulaire crée par une pointe vibrante qui se propage à la surface de l'eau est périodique.

La période temporelle $T$ de l'onde est la durée au bout de laquelle un point du milieu de propagation se retrouve dans le milieu état vibratoire. Cette période est égale à celle du vibreur.

Sa fréquence $f=\frac{1}{T}$

Ondes sonores

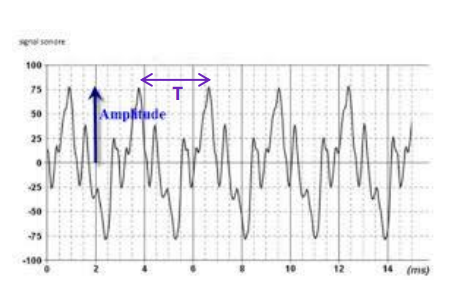
Le son émis par une guitare est une onde progressive périodique de période temporelle $\mathrm{T}$. Dans le cas d'un diapason, le son émis est une onde progressive sinusoïdale.

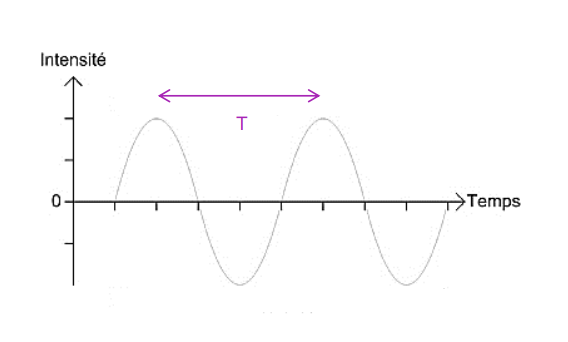
Double périodicité

Périodicité temporelle

La période T d'une onde progressive périodique est la durée minimale au bout de laquelle l'onde se répète identiquement à elle-même. Elle s'exprime en seconde (s).

On un point $x$ donné, $f(x, t)=f(x, t+T)$

Périodicité spatiale

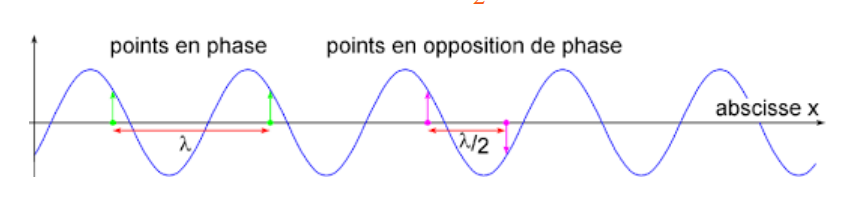
La longueur d'onde $\lambda$ d'une onde progressive périodique est la distance minimale séparant deux positions vibrant en phase.

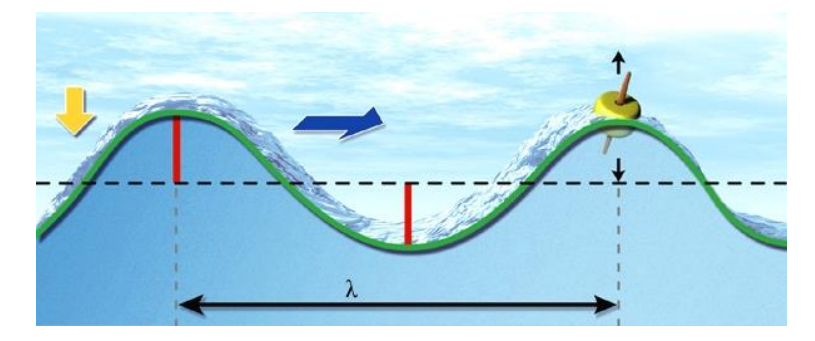
A un instant donné, on a: $f(x, t)=f(x+\lambda, t)$

Une onde progressive périodique présente une double périodicité :

Une périodicité temporelle, de période T ;
Une périodicité spatiale, de période $\lambda$.

Ondes progressives périodiques sinusoïdales

Définition

Une onde progressive périodique est sinusoïdale si son élongation s'écrit sous forme d'une fonction sinusoïdale : $$x(t)=X_m \cdot \cos \left(\frac{2 \pi}{T}t+\varphi\right)$$

$X_m$ : I'amplitude de l'onde

$T$ : période temporelle

$\varphi$ : phase à l'origine

Relation entre longueur d'onde et période

Pour une onde progressive périodique sinusoïdale, la longueur d'onde $\lambda$ est la distance parcourue par l'onde pendant une période $\mathrm{T}: \lambda=v \cdot T=\frac{v}{f}$ v étant la célérité de l'onde.

Etats vibratoires et longueur d'onde

a- Deux points $M_1$ et $M_2$ appartenant au même de milieu de propagation sont en phase si la distance qui les sépare est multiple entier de la longueur d'onde $\lambda: M_1 M_2=k \lambda$ k nombre entier.

A un instant $t$ donné

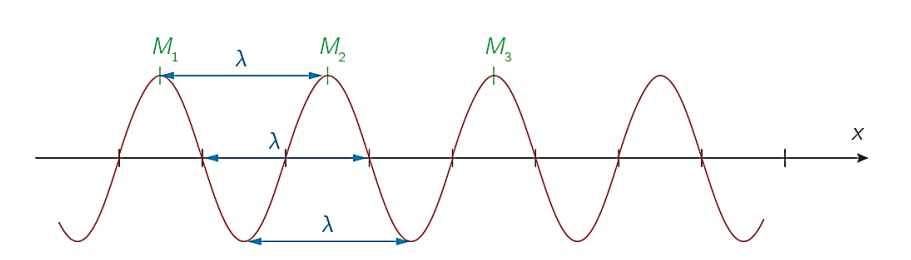
b- Deux points $M_1$ et $M_2$ appartenant au même milieu de propagation sont en opposition de phase si la distance qui les sépare est un multiple impair de la moitié de la longueur d'onde :

$$M_1 M_2=(2 k+1) \frac{\lambda}{2}$$