Rotation d'un solide indéformable autour d'un axe fixe 1BAC

Fiche de cours

Les deux photos montrent une balançoire pour enfant et la Grande Roue. Ces deux systèmes sont constitués par des corps solides qui ont un mouvement de rotation autour d’un axe fixe. Qu’est-ce qu’un mouvement de rotation ? et quelles sont ses caractéristiques ?

La différence entre un mouvement de translation et un mouvement de rotation

انتباه

Dorénavant on parlera toujours d’un système indéformable (un solide)

Décrire le mouvement d’un corps c’est connaître le mouvement de chacun de ses points.
L’ensemble des positions prises par un point au cours du mouvement est appelé trajectoire.

Un solide est en mouvement de translation lorsque tout segment joignant deux points quelconques de ce solide reste parallèle à lui-même.

انتباه

Tous les points du solide ont des trajectoires identiques.
Tous les points ont à chaque instant le même vecteur vitesse. (Même direction, même sens et même valeur)
Attention, à des instants différents, les vecteurs vitesses peuvent être différents.

Alors, pour un solide en translation, il nous suffit de connaître la trajectoire d’un de ses points pour avoir le mouvement du solide.

Un solide indéformable est dit en rotation autour d’un axe fixe si le mouvement de chacun de ses points est circulaire centré sur cet axe

et la trajectoire de ces points mobiles appartient au plan orthogonal avec l’axe de rotation.

Les aiguilles d’une montre, le tambour d’une machine à laver, une porte…

انتباه

Lorsqu’un solide est en rotation autour d’un axe fixe, les points de ce solide situés sur l’axe de rotation restent immobiles.
Chaque point du solide décrit un cercle centré sur l’axe dans un plan perpendiculaire à celui-ci.

L’angle θ décrit entre deux instants donnés est le même pour tous les points du solide, c’est l’angle de rotation du solide.

Etude d’un mouvement circulaire

Repérage d’un point d’un corps solide en mouvement de rotation

Si on travaille dans un plan, on choisit un plan R (O, i, j), et la position est alors déterminée par son abscisse ‘x’ et par son ordonné ‘y’.
Si on travaille dans l’espace, on prend un repère R (O, i, j, k), et la position est alors déterminée par les trois coordonnées x, y et z.

Abscisse angulaire

On appelle l’abscisse angulaire du point M à un instant t donné la valeur algébrique de l’angle $$\theta=\left(\left.\widehat{\overline{O M_{1}}, \overline{O M_{2}}}\right)\right.$$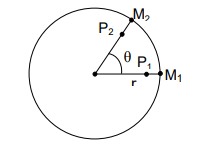

انتباه

Tous les points décrivent la même abscisse angulaire Ө(t) dans le même temps t.
L’unité de mesure de l’abscisse angulaire dans le système international des unités (SI) est le radian noté Rad.

Abscisse curviligne

Si la trajectoire que suit le point M est connue, il est possible de repérer le point M sur la courbe $\widehat{M_{1} M_{2}}$ représentant cette trajectoire.
On prend sur la courbe orientée selon le sens du mouvement un point origine A et on prend la direction de l’axe OM1 comme direction référentiel.
On définit l’abscisse curviligne s comme la mesure algébrique sur la courbe de l’arc s=$\widehat{AM}$ en mètre.

انتباه

L’abscisse curviligne est une fonction de temps, on écrit s(t).
Algébrique veut dire que la grandeur dont on parle possède un signe (positif ou négatif)

Relation entre s(t) et Ө(t)

On prend comme rayon de la trajectoire orientée du point M, la position de ce point sur cette trajectoire est définie grâce à son abscisse curviligne s(t) et de son abscisse angulaire Ө(t) qui sont reliés par la relation :

On prend R=OM comme rayon de la trajectoire orientée du point M, la position de ce point sur cette trajectoire est définie grâce à son abscisse curviligne s(t) et de son abscisse angulaire Ө(t) qui sont reliés par la relation :

$$s(t)=R \times \theta(t)$$

Vitesse angulaire

Au cours d’une rotation, plus un point est éloigné de l’axe, plus la longueur de l’arc décrit est grande : M1M2 > P1P2 car M plus loin de l’axe que P.
Les points du solide n’ont donc pas la même vitesse.

En revanche, ils décrivent tous le même angle, il est donc intéressant de caractériser le mouvement par la rapidité de la variation de cet angle. Pour cela on utilise la notion de vitesse angulaire.

D’où :

$$\omega_{\text {moy }}=\frac{\theta}{\Delta t}$$

$\omega_{\text {moy }}$ : vitesse angulaire moyenne (rad/s)
$\theta$ : Angle de rotation (rad)
$\Delta t$ : Durée de la rotation (s)

Pour avoir la vitesse angulaire instantanée, on procède comme pour une vitesse, on prend la vitesse angulaire moyenne entre deux instants très proches.