1. La valeur de la poussée est égale au poids du volume de fluide (l'air) déplacé :

$\mathrm{F}_{\mathrm{A}}=\rho_2 \cdot \mathrm{V} \cdot \mathrm{g}$

2. $\left\{\begin{array}{l}\mathrm{P}=\mathrm{m} \cdot \mathrm{g}=\rho_1 \cdot \mathrm{V} \cdot \mathrm{g} \\[0.2cm] \mathrm{F}_{\mathrm{A}}=\rho_2 \cdot \mathrm{V} \cdot \mathrm{g}\end{array} \Rightarrow \frac{\mathrm{P}}{\mathrm{F}_{\mathrm{A}}}=\frac{\rho_1}{\rho_2}=\frac{10^3}{1,3}=10^3 \times 0,77=770\right.$

Le poids est environ 800 fois supérieur à la poussée d'Archimède ; celle-ci peut être négligée devant le poids.$\\[0.5cm]$

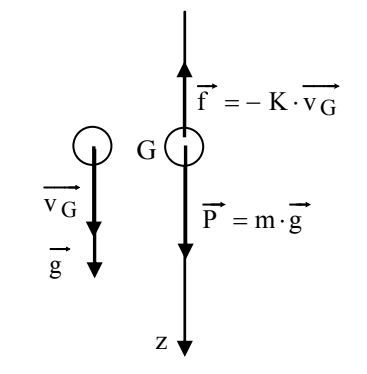
3.1. La goutte est soumise à son poids et à la force de frottement. Écrire la seconde loi de Newton sur un axe vertical orienté vers le bas :

$\mathrm{\vec{P}+\vec{f}=m \cdot \vec{g}}$

$\mathrm{m \cdot \vec{g}-K \cdot \overrightarrow{v_G}=m \cdot \frac{d}{d t} \overrightarrow{v_G}}$

$\longrightarrow \mathrm{m} \cdot \mathrm{g}-\mathrm{K} \cdot \mathrm{v}_{\mathrm{G}}=\mathrm{m} \cdot \frac{\mathrm{d}}{\mathrm{dt}} \mathrm{v}_{\mathrm{G}}$

$\longrightarrow \frac{\mathrm{d}}{\mathrm{dt}} \mathrm{v}_{\mathrm{G}}=-\frac{\mathrm{K}}{\mathrm{m}} \cdot \mathrm{v}_{\mathrm{G}}+\mathrm{g} \quad \longrightarrow\left\{\begin{array}{l}\mathrm{A}=-\frac{\mathrm{K}}{\mathrm{m}} \\ \mathrm{B}=\mathrm{g}\end{array}\right.\\[0.5cm]$

3.2. (B) a la dimension d'une accélération $\left(\mathrm{m} \cdot \mathrm{s}^{-2}\right)$

$\left(\mathrm{A} \cdot \mathrm{v}_{\mathrm{G}}\right)$ a la dimension d'une accélération et $\mathrm{v}_{\mathrm{G}}$ celle d'une vitesse $\left(\mathrm{m} \cdot \mathrm{s}^{-1}\right)$.

(A) est donc l'inverse d'un temps $\left(\mathrm{s}^{-1}\right).\\[0.5cm]$

3.3.1. On a :

$\begin{aligned}\mathrm{t}=3,4 \mathrm{~s} \longrightarrow ~\mathrm{a}_{\mathrm{G}}&=\frac{\mathrm{d}}{\mathrm{dt}} \mathrm{v}_{\mathrm{G}}\\[0.2cm] &=\mathrm{A} \cdot \mathrm{v}_{\mathrm{G}}+\mathrm{B} \\[0.2cm] &=-3,24 \cdot 10^{-1} \times 21,0+10 \\[0.2cm] &=3,196 \mathrm{~m} \cdot \mathrm{s}^{-2} \approx 3,2 \mathrm{~m} \cdot \mathrm{s}^{-2}\end{aligned}\\[0.5cm]$

3.3.2 $\mathrm{a}_{\mathrm{G}}\left(\mathrm{t}_{\mathrm{i}}\right)=\frac{\mathrm{v}_{\mathrm{G}}\left(\mathrm{t}_{\mathrm{i}+1}\right)-\mathrm{v}_{\mathrm{G}}\left(\mathrm{t}_{\mathrm{i}}\right)}{\Delta \mathrm{t}}$

$\Rightarrow \mathrm{v}_{\mathrm{G}}\left(\mathrm{t}_{\mathrm{i}+1}\right)=\mathrm{a}_{\mathrm{G}}\left(\mathrm{t}_{\mathrm{i}}\right) \cdot \Delta \mathrm{t}+\mathrm{v}_{\mathrm{G}}\left(\mathrm{t}_{\mathrm{i}}\right)$

$\begin{aligned} \Rightarrow \quad \mathrm{v}_{\mathrm{G}}(3,6 \mathrm{~s}) & =\mathrm{a}_{\mathrm{G}}(3,4 \mathrm{~s}) \cdot \Delta \mathrm{t}+\mathrm{v}_{\mathrm{G}}(3,4 \mathrm{~s}) \\ & =3,196 \times 0,2+21,0 \\&=21,6392 \mathrm{~m} \cdot \mathrm{s}^{-1} \approx 21,6 \mathrm{~m} \cdot \mathrm{s}^{-1}\end{aligned}\\[0.5cm]$

3.3.3. Le pas doit être petit. Généralement, on prend $\Delta t=\frac{\tau}{10}~$ ( $\tau$ est le temps caractéristique du mouvement)$\\[0.5cm]$

3.4.1. L'accélération est égale au coefficient directeur de la tangente à la courbe à une date donnée.

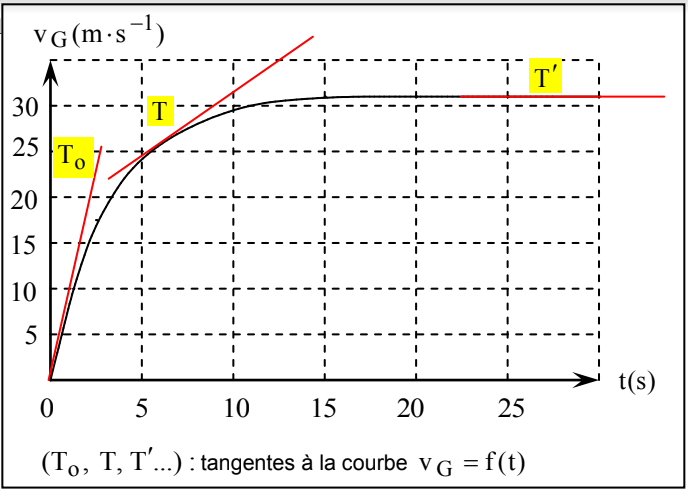
Or ces tangentes sont de moins en moins inclinées sur l'horizontale.

L'accélération diminue au cours du temps.$\\[0.5cm]$

3.4.2. En régime permanent, le mouvement est rectiligne uniforme et l'accélération est nulle.$\\[0.5cm]$

3.4.3 $\mathrm{m} \cdot \mathrm{g}-\mathrm{K} \cdot \mathrm{v}_{\mathrm{G} \lim }=\mathrm{m} \cdot \frac{\mathrm{d}}{\mathrm{dt}} \mathrm{v}_{\mathrm{G} \lim }=0$

$\mathrm{~K} \cdot \mathrm{v}_{\mathrm{G} \lim} =\mathrm{m} \cdot \mathrm{g}$ $\mathrm{v}_{\mathrm{G} \lim} =\frac{\mathrm{m}}{\mathrm{K}} \cdot \mathrm{g}$