CHIMIE

Partie I

1. $\mathrm{n}_{\mathrm{i}}=\frac{\mathrm{m}(\mathrm{HCOOH})}{\mathrm{M}(\mathrm{HCOOH})}=\frac{\rho \cdot \mathrm{V}}{\mathrm{M}(\mathrm{HCOOH})}$

Avec $~~\mathrm{V}=\frac{50}{100} \times \mathrm{V}_{\mathrm{i}}=\frac{\mathrm{V}_{\mathrm{i}}}{2}$,

on a : $~~\mathrm{n}_{\mathrm{i}}=\frac{\rho \cdot\left(\frac{\mathrm{V}_{\mathrm{i}}}{2}\right)}{\mathrm{M}(\mathrm{HCOOH})}=\frac{1,22 \times\left(\frac{6 \cdot 10^{-3}}{2}\right)}{46,0} \approx 7,96 \cdot 10^{-2} \mathrm{mol}\\[0.5cm]$

2. Réaction avec les ions hydrogénocarbonate :

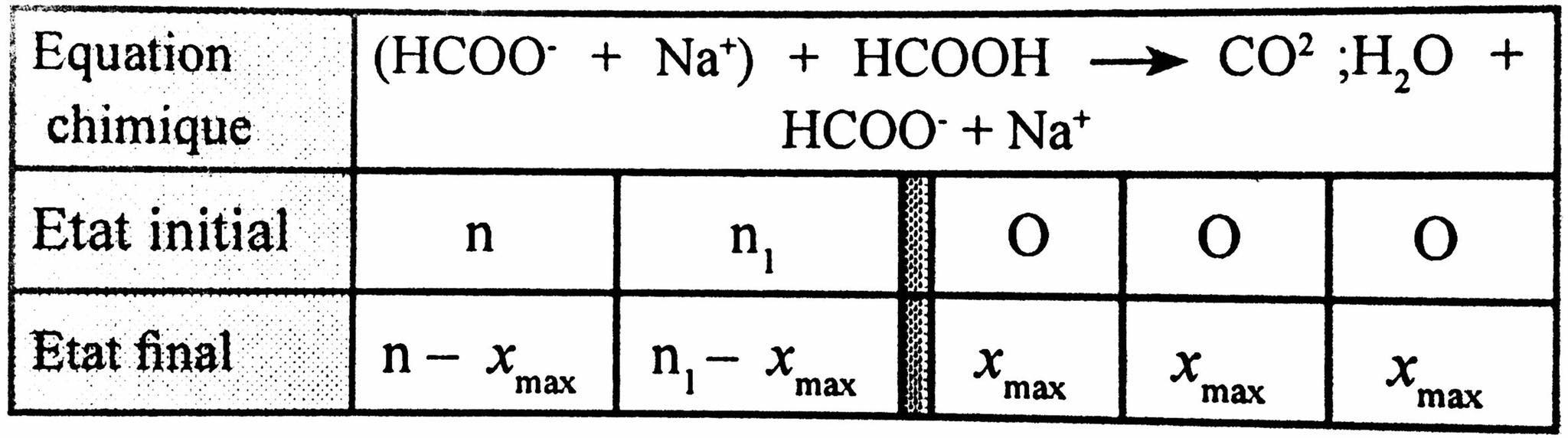
2.1. $\left(\mathrm{HCOO}^{-}+\mathrm{Na}^{+}\right)+\mathrm{HCOOH} \longrightarrow \mathrm{CO}_2 ; \mathrm{H}_2 \mathrm{O}+\mathrm{HCOO}^{-}+\mathrm{Na}^{+}\\[0.5cm]$

2.2- Masse de l'hydrogénocarbonate:

* Tableau d'avancement

La réaction est totale et stoechiometique ;

donc: $~~\mathrm{n}_1-x_{\max }=0 \Rightarrow x_{\max }=\mathrm{n}_1=7,96 \times 10^{-5}\mathrm{~mol}$

et $: ~~\mathrm{n}-x_{\max }=0 \Rightarrow \mathrm{n}=x_{\max }=7,96 \times 10^{-5} \mathrm{~mol}$.

On sait que $:~~ \mathrm{n}=\frac{\mathrm{m}}{\mathrm{M}}:$

soit $:~~ \mathrm{m}=\mathrm{n} \times \mathrm{M}$

Donc : $~~\mathrm{m}=7,96 \times 10^{-5} \times 84=6,686 \times 10^{-3} \mathrm{~g}$

Soit : $~~\mathrm{m}=6,7 \mathrm{mg}.\\[0.5cm]$

3- Réaction de l'acide méthanoïque avec l'eau :

3.1. Le volume de la solution $S_2$ est : $~~V_2=1,00 \mathrm{~mL}=1,00 \cdot 10^{-3} \mathrm{~L}$

La concentration de la solution $\mathrm{S}_2$ est :

$\mathrm{C}_2=\frac{\mathrm{n}_{\mathrm{i}}}{\mathrm{V}_2}=\frac{7,96 \cdot 10^{-2} \cdot 10^{-3}}{1,00 \cdot 10^{-3}}=7,96 \cdot 10^{-2} \mathrm{~mol} \cdot \mathrm{L}^{-1}$

Pourcentage :

$\mathrm{P}=\frac{\mathrm{n}(\mathrm{HCOOH}) \text { ayant réagi }}{\mathrm{n}(\mathrm{HCOOH}) \text { initiale }}=\frac{\mathrm{n}\left(\mathrm{HCOO}^{-}\right) \text {formée }}{\mathrm{n}(\mathrm{HCOOH}) \text { initiale }}=\frac{\mathrm{x}_{\mathrm{f}}}{\mathrm{x}_{\max }}=\tau$

$$\tau=\frac{\mathrm{x}_{\mathrm{f}}}{\mathrm{x}_{\max }}=\frac{\mathrm{x}_{\mathrm{f}}}{\mathrm{n}_{\mathrm{i}}}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \cdot \mathrm{V}_2}{\mathrm{n}_{\mathrm{i}}}=\frac{10^{-\mathrm{pH}} \cdot \mathrm{V}_2}{\mathrm{n}_{\mathrm{i}}}=\frac{10^{-2,43} \times 1,00 \cdot 10^{-3}}{7,96 \cdot 10^{-2} \cdot 10^{-3}}=4,67 \%$$

Donc la réaction n'est pas totale et l'équation de cette réaction s'écrit avec double flèche :

$$\mathrm{HCOOH}_{(\mathrm{aq})}+\mathrm{H}_2 \mathrm{O}_{(\mathrm{l})} \rightleftarrows \mathrm{HCOO}_{(\mathrm{aq})}^{-}+\mathrm{H}_3 \mathrm{O}_{(\mathrm{aq})}^{+}\\[0.5cm]$$

3.2- Calcul du $\mathrm{pK_A}$ du couple :

$\mathrm{pH}=\mathrm{pK}_{\mathrm{A}}+\log \frac{\left[\mathrm{HCOO}^{-}\right]_{\text {éq }}}{[\mathrm{HCOOH}]_{\text {éq }}}$

$\left\{\begin{array}{l}{\left[\mathrm{HCOO}^{-}\right]_{\text {éq }}=\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_{\text {éq }}=10^{-\mathrm{pH}}} \\ {[\mathrm{HCOOH}]_{\text {éq }}=\frac{\mathrm{n}_{\mathrm{i}}-\mathrm{x}_{\mathrm{f}}}{\mathrm{V}_2}=\frac{\mathrm{n}_{\mathrm{i}}}{\mathrm{V}_2}-\frac{\mathrm{x}_{\mathrm{f}}}{\mathrm{V}_2}=\mathrm{C}_2-\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_{\text {éq }}}\end{array}\right.$

$\begin{aligned}\mathrm{pK}_{\mathrm{A}}=\mathrm{pH}-\log \left(\frac{\left[\mathrm{HCOO}^{-}\right]_{\text {eq }}}{[\mathrm{HCOOH}]_{\text {eq }}}\right)&=\mathrm{pH}-\log \left(\frac{10^{-\mathrm{pH}}}{\mathrm{C}_2-10^{-\mathrm{pH}}}\right)\\ &=2,43-\log \left(\frac{10^{-2,43}}{7,96 \cdot 10^{-2}-10^{-2,43}}\right)=3,74 \end{aligned}\\[0.5cm]$

4- Solution aqueuse $S_3$ d'acide méthanoïque :

La concentration de la solution $\left(\mathrm{S}_3\right)$ est :

$$\mathrm{C_3=\frac{n_1}{v}}=\frac{7,96 \times 10^{-5}}{1 \times 10^{-3}}=7,96 \times 10^{-2} \mathrm{~mol} \cdot \mathrm{L}^{-1}\\[0.5cm]$$

4-1- On dilue la solution $\mathrm{S}_3$ pour avoir une solution $\left(\mathrm{S}_3^{\prime}\right)$ de concentration molaire :

$$\mathrm{C}_3^{\prime}=\frac{\mathrm{C}_3}{3}=\frac{7,96 \times 10^{-2}}{3}=2,65 \times 10^{-2} \mathrm{~mol} \cdot \mathrm{L}^{-1}$$

- Calcul du pH de cette solution :

On a : $~~\mathrm{pK}_{\mathrm{A}}=\frac{\left.17,5 \times 10^{-3}[\mathrm{HCOO}\right] \times\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{[\mathrm{HCOOH}]}=\frac{\mathrm{C}_3^{\prime} \times\left(\tau^{\prime}\right)^2}{1-\tau^{\prime}}$

Soit : $~~\mathrm{k}_{\mathrm{A}} \approx \mathrm{C}_3^{\prime} \times\left(\tau^{\prime}\right)^2$

Avec $: ~~\tau^{\prime}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{\mathrm{C}_3^{\prime}}$

D'où : $~~\mathrm{k}_{\mathrm{A}}=\mathrm{C}_3^{\prime} \times\left(\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{\mathrm{C}_3^{\prime}}\right)^2=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]^2}{\mathrm{C}_3^{\prime}}$

Donc: $~~\left[\mathrm{H}_3 \mathrm{O}^{+}\right]^2=\mathrm{k}_{\mathrm{A}} \times \mathrm{C}_3^{\prime}$

Soit : $~~\left[\mathrm{H}_3 \mathrm{O}^{+}\right]^2=\sqrt{\mathrm{k}_{\mathrm{A}} \times \mathrm{C}_3^{\prime}}$

Et : $~~\mathrm{pH}=-\log \left[\mathrm{H}_3 \mathrm{O}^{+}\right]=-\log \sqrt{\mathrm{k}_{\mathrm{A}} \times \mathrm{C}_3^{\prime}}$

Donc: $\quad \mathrm{pH}=-\frac{1}{2} \cdot \log \left(\mathrm{K}_{\mathrm{A}} \times \mathrm{C}_3^{\prime}\right)$

$\begin{aligned} \text { A.N : }~~ \mathrm{pH} & =-\frac{1}{2} \times \log \left(10^{-3,74} \times 2,65 \times 10^{-2}\right) \\ \mathrm{pH} & \approx 2,66\end{aligned}\\[0.5cm]$

4-2-Réaction de l'acide formique avec la soude :

4-2-1-Équation de la réaction :

$\mathrm{HCOOH}+\mathrm{HO}^{-} \longrightarrow \mathrm{HCOO}^{-}+\mathrm{H}_2 \mathrm{O}\\[0.5cm]$

4-2-2- Calcul du $\mathrm{pH}$ de cette solution :

On a la relation : $~~\mathrm{pH}=\mathrm{pk}_{\mathrm{A}}+\log \left(\frac{\left[\mathrm{HCOO}^{-}\right]}{[\mathrm{HCOOH}]}\right)$

- tableau d'avancement :

On a à l'état final :

$C_{\mathrm{A}} \cdot \mathrm{V}_{\mathrm{A}}-x_{\max }=0 \Rightarrow x_{\max }=\mathrm{C}_{\mathrm{A}} \cdot \mathrm{V}_{\mathrm{A}}=\mathrm{C}_3 \times \mathrm{V}_{\mathrm{A}}$

Soit : $~~\mathrm{x}_{\max }=7,96 \times 10^{-2} \times 10 \times 10^{-3}=7,96 \times 10^{-4} \mathrm{~mol} .$

$ \mathrm{C}_{\mathrm{b}} \cdot \mathrm{V}_{\mathrm{b}}-x_{\max }=0 \Rightarrow x_{\max }=\mathrm{C}_{\mathrm{b}} \cdot \mathrm{V}_{\mathrm{b}}$

Soit : $~~\mathrm{x}_{\max }=7,5 \times 10^{-3} \times 0,1=7,5 \times 10^{-4} \mathrm{~mol}$.

Donc : $~~\mathrm{HO}^{-}~$ est le réactif limitant et $~\mathrm{x}_{\max }=7,5 \times 10^{-4} \mathrm{~mol}$.

D'où : $~~[\mathrm{HCOO}^-]=\frac{x_{\max }}{\mathrm{V}}=\frac{7,5 \times 10^{-4}}{17,5 \times 10^{-3}} \approx 4,3 \times 10^{-2} \mathrm{~mol} / \mathrm{L}$

Et $:~~[\mathrm{HCOOH}]=\frac{\mathrm{C}_{\mathrm{A}} \cdot \mathrm{V}_{\mathrm{A}}-x_{\max }}{\mathrm{V}}=\frac{7,96 \times 10^{-4}-7,5 \times 10^{-4}}{17,5 \times 10^{-3}}=2,63 \times 10^{-3} \mathrm{~mol} \cdot \mathrm{L}^{-1}$.

Donc $:~~ \mathrm{pH}=3,74+\log \left(\frac{4,3 \times 10^{-2}}{2,63 \times 10^{-3}}\right) \approx 4,95.\\[0.5cm]$

Partie II :Pile plomb-fer

1-Les propositions fausses sont au nombre de 3 .(a ; b ; et d )$\\[0.5cm]$

2- Équation chimique :

À l'anode on a: $~~\mathrm{Fe}_{(\mathrm{s})} \rightleftharpoons \mathrm{Fe}_{(\mathrm{aq})}^{2+}+2 \mathrm{e}^{-}$

À le cathode on a $: ~~\mathrm{Pb}_{(\mathrm{aq})}^{2+}+2 \mathrm{e}^{-} \mathrm{Pb}_{(\mathrm{s})}$

Équation bilan : $~~\mathrm{Fe}(\mathrm{s})+\mathrm{Pb}_{(\mathrm{aq})}^{2+} \rightleftharpoons \mathrm{Fe}_{(\mathrm{aq})}^{2+}+\mathrm{Pb}_{(\mathrm{s})}\\[0.5cm]$

3-Quotient de réaction à l'imitant $\mathrm{t}_1$ :

On a: $~~\mathrm{Qr_1} =\frac{\left[\mathrm{Fe}^{2+}\right]_1 \times[\mathrm{Pb}]_1}{\left.[\mathrm{Fe}]_1 \times [\mathrm{Pb}^{2+}\right]_1}=\frac{\left[\mathrm{Fe}^{2+}\right]_1}{\left[\mathrm{~Pb}^{2+}\right]_1}$

- tableau d'avancement :

À l'instant $\mathrm{t}_1 ;$

on a $~~x_1=\mathrm{n}_1(\mathrm{~Pb})=\frac{\mathrm{m}}{\mathrm{M}}$

Soit : $~~x_1=\frac{2,07 \times 10^{-3}}{207}=10^{-5} \mathrm{~mol}$.

D'après le tableau d'avancement :

$$\left[\mathrm{Fe}^{2+}\right]_1=\frac{\left[\mathrm{Fe}^{2+}\right]_{\mathrm{i}} \times \mathrm{V}+x_1}{\mathrm{~V}}~~ \text { et }~~\left[\mathrm{Fe}^{2+}\right]_1=\frac{\left[\mathrm{Pb}^{2+}\right]_{\mathrm{i}} \times \mathrm{V}-x_1}{\mathrm{~V}}$$

d'où : $~~Qr_1 =\frac{\left[\mathrm{Fe}^{2+}\right]_{\mathrm{i}} \times \mathrm{V}+x_1}{\left[\mathrm{~Pb}^{2+}\right]_{\mathrm{i}} \times \mathrm{V}-x_1}$

soit : $~~Qr_1=\frac{4 \times 10^{-2} \times 0,1+10^{-5}}{1 \times 10^{-3} \times 0,1-10^{-5}}=44,56.\\[0.5cm]$

4- Calcul de l'instant $t_1$ :

On a: $~~\mathrm{I}_0 \times \Delta \mathrm{t}=\mathrm{n}_1\left(\mathrm{e}^{-}\right) \times \mathrm{F}$

soit: $~~\Delta t=\frac{n_1(e) \times F}{I_0}=\frac{n_1\left(e^{-}\right) \times F}{I_0}=\frac{2 \times x_1 \times F}{I_0}$

avec $: ~~\Delta \mathrm{t}=\mathrm{t}_1-\mathrm{t}_0=\mathrm{t}_1$

ainsi : $$~~~t_1=\frac{2 \times x_1 \times \mathrm{F}}{I_0}$$

A.N: $~~~t_1=\frac{2 \times 10^{-5} \times 9,65 \times 10^4}{2 \times 10^{-3}}=965 \mathrm{~s}$