CHIMIE :
Partie I : Pile diode - zinc
1-Sens d'évolution du système chimique :
Le quotient de réaction à l'état initial s'écrit :
Qr,i=[I2]i[I−]i2×[Zn2+]i=0,1(5×10−2)2×0,1=2,5×10−3
On a : K=1046
Alors : Qr,i,i≪K donc le système évolu spontanément dans le sens direct (sens)(1)).
2- Au niveau de la cathode; il se produit une réduction d'équation:
I2(aq)+2e−⇌2I(aq)−
3-Selon l'équation du dosage on a :
I2(aq)+2 S2O3(aq)2−⟶2I(aq)−+S4O6(aq)2−
Soit à l'équivalence : n(I2)=2n( S2O32−)=2Cr×VE
Soit : n(I2)=21×0,3×20×10−3=3×10−3 mol
La quantité de matière de I2 consommée lors du fonctionnement de la pile est nc(I2), telle que :
ni(I2)=nc(I2)+n(I2)
Soit : nc(I2)=ni(I2)−n(I2)=c1×V−n(I2)
D'où : nc(I2)=0,1×0,1−3×10−3=7×10−3 mol.
Soit : nc(I2)=7 m mol.
4-Durée du fonctionnement de la pile:
On a la relation : I0×Δt=n(e−)×F
Donc : Δt=I02.x×F
*Tableau d'avancement:

D'après le tableau d'avancement, on a :
x=nc(I2)
D'où : Δt=I02×nc(I2)×F
Ainsi : Δt=70×10−32×7×10−3×9,65×104=19300 S.
5-Concentration molaire des ions zinc :
[Zn2+]=Vn(Zn2+)=VC0⋅V+x
Soit [Zn2+][Zn2+]=C0+Vx=C0+Vn(Zn2+)=0,1+0,17×10−3=0,17 mol⋅L−1.
Partie II :
1-Équation du dosage :
CnH2n+1COOH+HO−⟶CnH2n+1COO−+H2O
2-A l'équivalence on a la relation :
CA×VA=CB×VBE
Soit : CA=VACB×VBE A.N: CA=100,1×10=0,1 mol⋅L−1
La quantité de matière de l'acide dans le volume V=500 mL est donnée pour la relation :
n(A)=CA×V=Mm
D'où : M=CA×Vm=0,1×0,52,3=46 g/mol
Et on a également : M=M(CnH2n+1COOH)
M=M(C)×n+M(H)×(2n+1)+M(C)+2×M(O)+M(H)
⇒46=12×n+2n+1+12+2×16+1
⇒46=14n+46
Soit : n=0 D'où la formule brute de l'acide : HCOOH.
3-Étude de la solution (S) :
3.1-Taux d'avancement final :
τ=xmaxxf=CA×V[H3O+]×V=CA[H3O+]
Soit : τ<1 donc la réaction de l'aide méthanoïque avec l'eau est limitée.
3.2- Valeur du rapport :
On a à l'équilibre:
[HCOO−]eˊq=[H3O+]eˊq= Vxf
Et : [HCOOH]eˊq= VCA⋅V−xf=CA− Vxf=CA−[H3O+]
D'où : [HCOOH]eˊq[HCOO−]eˊq=CA−[H3O+][H3O+]eˊq=CA−10−pH10−pH
[HCOOH]eˊq[HCOO−]eˊq=0,1−10−2,3810−2,38≈0,044.
3.3 - Valeur du pKA:
On a : pH=pKA+log[HCOOH][HCOO−]
Donc : pHA=pH−log[HCOOH][HCOO−]
Donc : pHA=2,38−log(0,044)≈3,74.
4 - Tableau d'avancement:
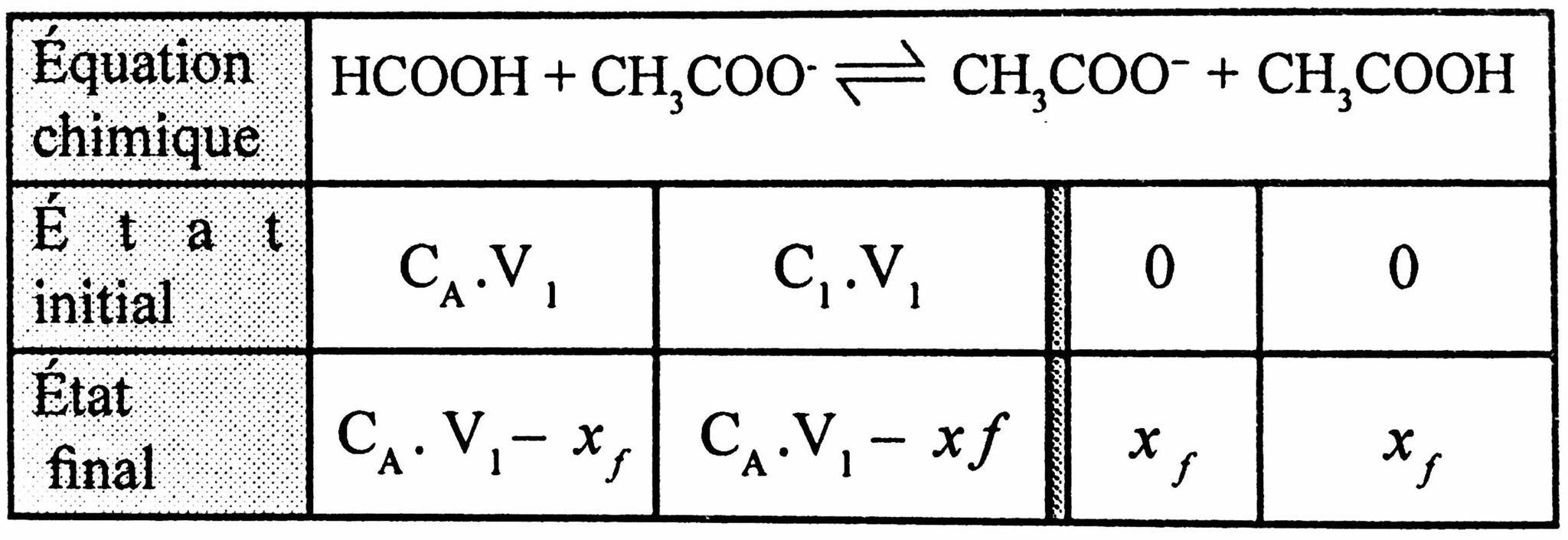
On a : pH=pHA1+log[HCOOH]eˊq[HCOO+]eˊq
pH=pHA2+log[CH3COOH]eˊq[CH3COO−]eˊq
d'où
2pH=pHA1+pHA2+log[HCOOH][HCOO−]+log[CH3COOH][CH3CO]
⇒2pH=pHA1+pHA2+log[HCOOH]×[CH3COOH][HCOO−]×[CH3COO−]
d'après le tableau d'avancement ; on a à l'équilibre :
[HCOO−]=[CH3COOH]=2 V1xf
[HCOO−]=[CH3COO−]=2 V1CA⋅V1−xf
D'où : log[HCOOH]×[CH3COOH][HCOO−]×[CH3COO−]=0
Donc : 2pH=pHA1+pHA2
Soit : pH=21⋅(pHA1+pHA2)
Valeur de pKA2 :
On a : 2pH=pKA1+pKA2 donc : pKA2=2⋅pH−pKA1
A.N : pKA2=2×4,25−3,74=4,76