CHIMIE :

Partie I : Dosage acido-basique

1- Coordonnées du point d'équivalence :

$V_E=10~ml \quad$ et $\quad \mathrm{pH_E}=6.3\\[0.5cm]$

2- A l'équivalence du dosage on a : $~~C \cdot V =C_A \cdot V_E$

D'où $~~\mathrm{C=\frac{C_A \cdot V_E}{V}=\frac{2 \times 10^{-2} \times 10}{10}}$

Soit $~~\mathrm{C=2 \times 10^{-2}~mol.L^{-1}}\\[0.5cm]$

3- L'indicateur coloré qui convient pour ce dosage est le bleu de bromothymol puisque sa zone de virage contient le $\mathrm{pH_E}$: $~~6< \mathrm{pH_E} < 7.6 \\[0.5cm]$

4- Equation chimique du dosage:

$\mathrm{CH_3NH_{2(aq)}+H_3O^{+}_{(aq)}\longrightarrow CH_3NH^{+}_{3(aq)}+H_2O^{+}_{(\ell)}}\\[0.5cm]$

5- * Tableau d'avancement:

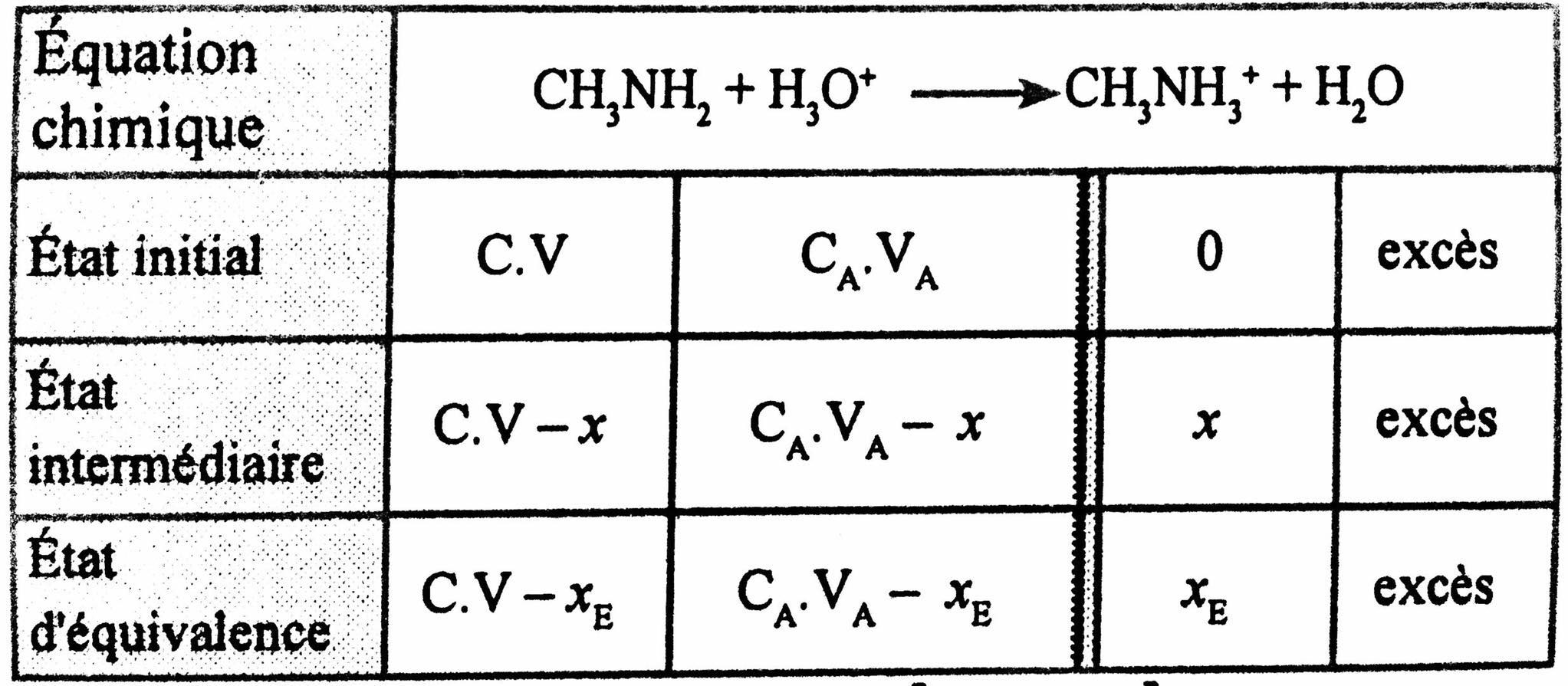
On a la relation : $~\mathrm{pH=pK_{A_1}+\log \frac{[CH_3NH_2]}{[CH_3NH^{+}_{4}]}}$

Pour : $~\mathrm{V_A < V_E}~$ et d'aprés le tableau d'avancement :

$\mathrm{[CH_3NH_2]=\frac{C \cdot V -x}{V +V_A}} \quad$ et $\quad \mathrm{[CH_3NH^{+}_{4}]=\frac{x}{V+V_A}}$

Ainsi : $~\mathrm{pH=pK_{A_1}+\log (\frac{C_A \cdot V_E}{C_A \cdot V_A}-1)}$

$\mathrm{pH=pK_{A_1}+\log (\frac{V_E}{V_A}-1)}$

On a : $~\mathrm{y=\frac{V_A}{V_E}}~$

donc $~\mathrm{\frac{V_E}{V_A}=\frac{1}{y}}$

Donc : $~\mathrm{pH=pK_{A_1}+\log(\frac{1}{y}-1)}\\[0.5cm]$

6- Valeur de $\mathrm{y}$ :

On a : $~\mathrm{pH=pK_{A_1}+\log (\frac{1}{y}-1)}$

Avec : $~ \mathrm{pH=pK_{A_1}}~$ cette relation devient :

$\mathrm{pK_{A_1}+\log (\frac{1}{y}-1)=pK_{A_1}}~$ soit $~\mathrm{\log (\frac{1}{y}-1)=0}$

D'où : $~\mathrm{\frac{1}{y}-1=1}~$ soit $~\mathrm{\frac{1}{y}=2}~$

Donc : $~~\mathrm{y=\frac{1}{2}=0.5}$

* Valeur du $\mathrm{pK_{A_1}}$ :

On a : $~~\mathrm{y=\frac{V_A}{V_E}=\frac{1}{2}}~$ soit $~~\mathrm{V_A=\frac{V_E}{2}=5~mL}$

D'aprés la courbe de la figure 1 ; $~\mathrm{pK_{A_1}},~$ est la valeur du $\mathrm{pH}$ pour $\mathrm{V_A=5~mL}$ :

Soit $~\mathrm{pK_{A_1}=10.55}.\\[0.5cm]$

7- Etude de la solution (S) dosée :

7-1. Equation de la réaction de la methylamine avec l'eau :

$CH_3NH_{2(aq)} + H_2O \rightleftharpoons CH_3NH^{+}_{3(aq)} + HO^{-}_{(aq)}\\[0.5cm]$

7.2- Taux d'avancement final :

$\tau=\frac{x_f}{x_{max}}=\mathrm{\frac{[HO^{-}]\times V}{C \times V}=\frac{[HO^{-}]}{C}}$

Avec $~~\mathrm{[HO^{-}]=\frac{Ke}{[H_3O^+]}=\frac{Ke}{10^{-pH}}}$

D'où $~~\mathrm{\tau=\frac{Ke}{C \times 10^{-pH}}=\frac{10^{-11.4}}{(2\times 10^{-2})\times 10^{-11.4}}}$

$\tau = 0.125\\[0.2cm]$

(Remarque : le pH de cette solution est $~\mathrm{pH}=11.~$ à partir de la courbe de la figure 1).

Conclusion : On a : $~\tau<1~$ la réaction est limitée.$\\[0.5cm]$

Partie II : Hydrolyse basique d'un ester

1- Formule semi-développée de l'éthanoate de propyle :

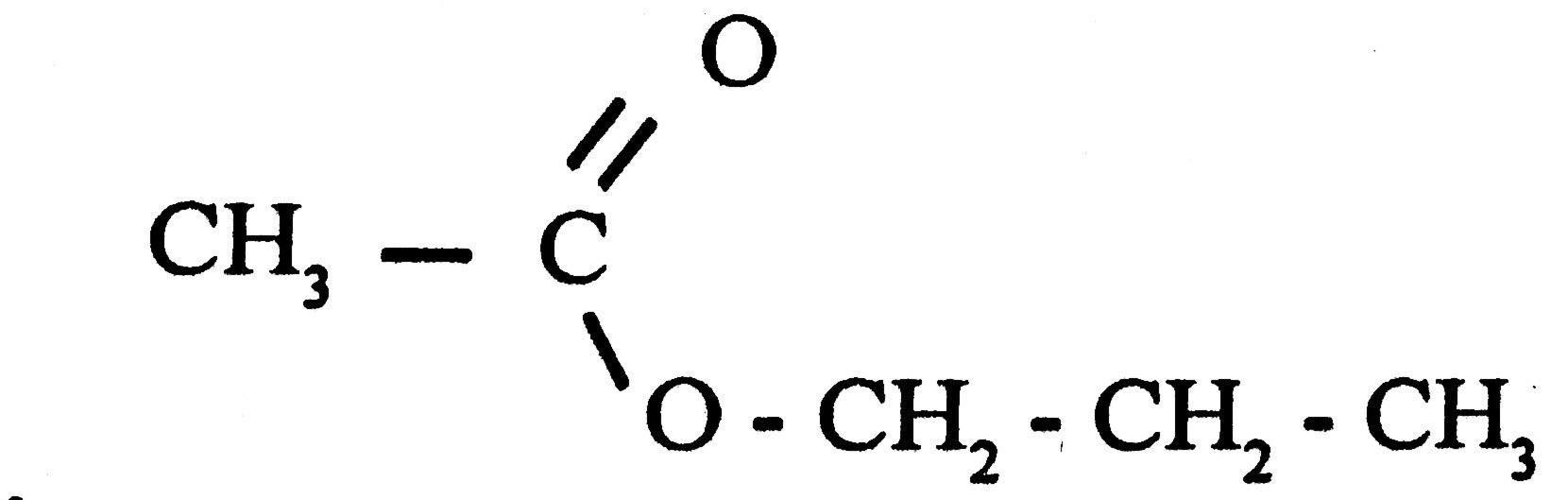
2- Evolution temporelle de cette réaction:

2.1- Le temps $t_{1/2}$ de demi-réaction est l'abscisse du point qui correspond à la moitié de la valeur maximale de la concentration de $\mathrm{CH_3COO^{-}_{(aq)}}$

Graphiquement et par projection on obtient :

$\mathrm{t}_{1 / 2}=4,8 \mathrm{~min}.\\[0.5cm]$

2.2-Pour la courbe $\mathrm{C}^{\prime}$ on a $~\mathrm{t}_{1 / 2}^{\prime} \approx 1,6 \mathrm{~min}$

On a: $~\mathrm{t}_{1 / 2}<\mathrm{t}_{1 / 2}$

On sait que plus la température augmente; la vitesse volumique de réaction augmente et le temps de demi-réaction diminu. Ainsi la courbe $\mathrm{C}^{\prime}$ correspond à la température $\theta_2\\[0.5cm]$

2.3-Vitesse volumique de réaction à $~t=0$ :

On a : $~\mathrm{V}=\frac{1}{\mathrm{~V}} \cdot \frac{\mathrm{d} x}{\mathrm{dt}}$

D'après l'équation de la réaction on a :

$$\left[\mathrm{CH}_3\mathrm{COO}^{-}\right]=\frac{x}{V}~~ \text { soit } ~~x=\left[\mathrm{CH}_3 \mathrm{COO^{-}}\right] \times \mathrm{V}$$

Ainsi : $~~\mathrm{V}=\frac{\mathrm{d}\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right]}{\mathrm{dt}}$

D'où : $~~V(t=0)=\frac{2,2-0}{4-0}=0,55 \mathrm{~m} \mathrm{~mol} \cdot \mathrm{L}^{-1} \cdot \mathrm{min}^{-1}.\\[0.5cm]$

2.4- Quotient de réaction à $t_{1 / 2}$ :

$$\mathrm{Qr}=\frac{\left[\mathrm{CH}_3 \mathrm{COO}^-\right] \times[\mathrm{A}]}{[\mathrm{E}] \times\left[\mathrm{HO}^-\right]}$$

* Tableau d'avancement de la réaction :

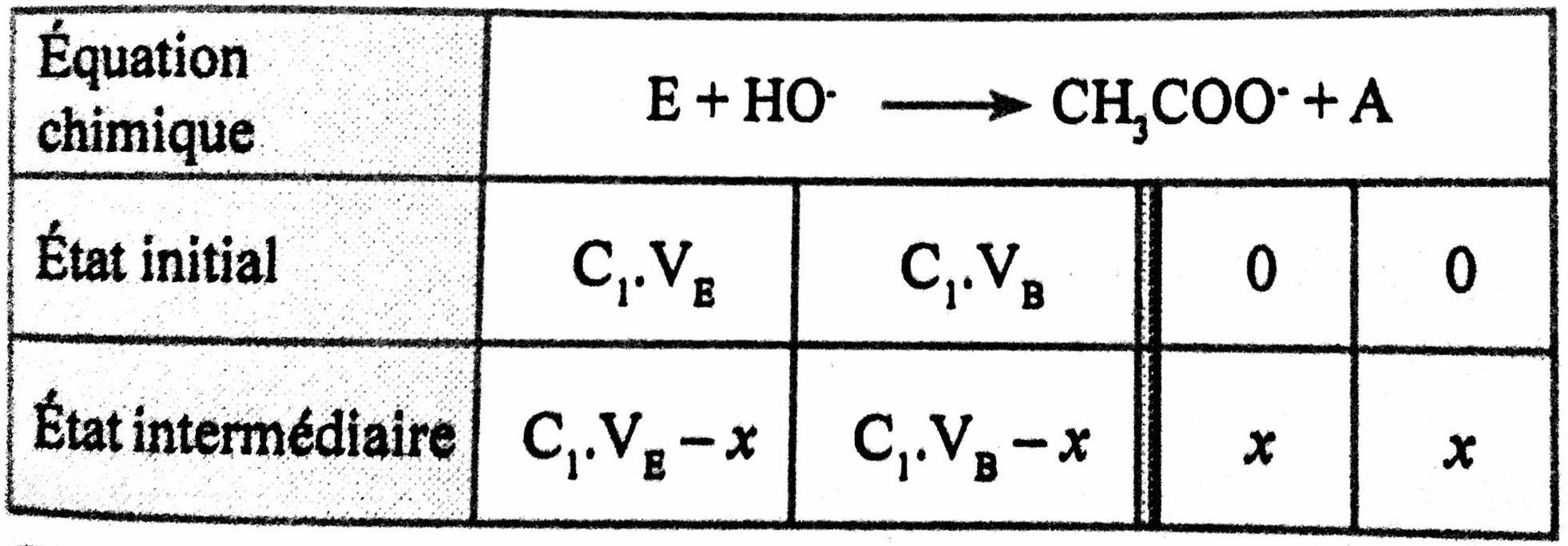
D'après le tableau d'avancement ; On a :

$$\begin{aligned}& {\left[\mathrm{CH}_3 \mathrm{COO}^-\right]=[\mathrm{A}]=\frac{x}{\mathrm{~V}}} \\[0.2cm]& {[\mathrm{E}] =\left[\mathrm{HO}^{-}\right]=\frac{\mathrm{C}_1 \cdot \mathrm{V}_{\mathrm{E}}-x}{\mathrm{~V}}=\frac{\mathrm{C}_1 \cdot \mathrm{V}_{\mathrm{E}}}{\mathrm{V}}-\frac{x}{\mathrm{~V}}}\end{aligned}$$

Avec: $\quad \mathrm{V}=\mathrm{V}_{\mathrm{E}}+\mathrm{V}_{\mathrm{B}}=2 \mathrm{~V}_{\mathrm{E}}$

$\begin{aligned}\text{D'où}:~[\mathrm{E}]=\left[\mathrm{HO}^-\right]& = \frac{\mathrm{C}_1 \times \mathrm{V}_{\mathrm{E}}}{2 \mathrm{~V}_{\mathrm{E}}}-\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right] \\[0.2cm] & =\frac{\mathrm{C}_1}{2}-\left[\mathrm{CH}_3 \mathrm{COO}^-\right]\end{aligned}$

Ainsi : $~~\mathrm{Qr}=\frac{\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right]^2}{\left(\frac{\mathrm{C}_1}{2}-\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right]\right)^2}$

A $\mathrm{t}_{1 / 2}~$ On a :$~\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right]=2 \times 10^{-3} \mathrm{~mol} \cdot \mathrm{L}^{-1}$

$\mathrm{Qr}=\frac{\left(2 \times 10^{-3}\right)^2}{\left(\frac{10^{-2}}{2}-2 \times 10^{-3}\right)^2}=0,44 \\[0.5cm]$

2.5- Rendement de cette réaction :

$\mathrm{r}=\frac{x f}{x_{\max }}$

On a d'après le tableau d'avancement :

$\left[\mathrm{CH}_3 \mathrm{COO}^-\right]_f=\frac{x f}{\mathrm{~V}}$

soit :$~ x f=\left[\mathrm{CH}_3 \mathrm{COO}^- \right]_f \times \mathrm{V}$

$\mathrm{C}_1 \cdot \mathrm{V}_{\mathrm{E}-x_{\max }}=0~~$ soit : $~~x_{\max }=\mathrm{C}_1 \times \mathrm{V}_{\mathrm{E}} $

D'où : $~~\tau=\frac{\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right]_f \times \mathrm{V}}{\left.\mathrm{C}_1 \times \mathrm{V}_{\mathrm{E}}\right.}=\frac{\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right]_f \times 2 \times \mathrm{V}_{\mathrm{E}}}{\mathrm{C}_1 \times \mathrm{V}_{\mathrm{E}}}$

Donc : $~~\tau=\frac{2 \times\left[\mathrm{CH}_3 \mathrm{COO}^-\right]_f}{\mathrm{C}_1}$

Graphiquement : $~\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right]_f=4 \times 10^{-3} \mathrm{~mol} . \mathrm{L}^{-1}$

$\tau=\frac{2 \times 4 \times 10^{-3}}{10^{-2}}=0,8=80 \%$