L'atome et la mécanique de Newton

Comparaison système planétaire - atome

Forces newtoniennes

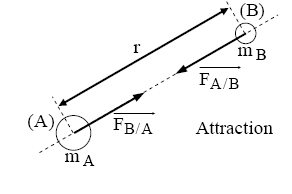
Interaction gravitationnelle :
$$\overrightarrow{\mathrm{F}_{\mathrm{B} / \mathrm{A}}}=-\overrightarrow{\mathrm{F}_{\mathrm{A} / \mathrm{B}}} \text { et } \mathrm{F}=\mathrm{G} \cdot \frac{\mathrm{m}_{\mathrm{A}} \cdot \mathrm{m}_{\mathrm{B}}}{\mathrm{r}^2}$$

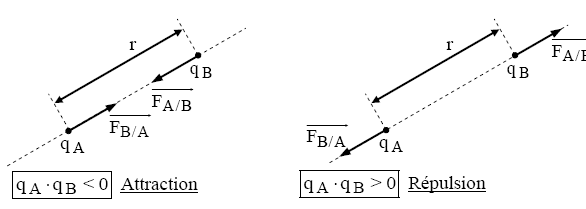
Interaction électrostatique : $\overline{\mathrm{F}_{\mathrm{B} / \mathrm{A}}}=-\overline{\mathrm{F}_{\mathrm{A} / \mathrm{B}}}$ et $\mathrm{F}=\mathrm{k} \cdot \frac{\left|\mathrm{q}_{\mathrm{A}}\right| \cdot\left|\mathrm{q}_{\mathrm{B}}\right|}{\mathrm{r}^2}$

- Dans un atome, c'est l'interaction électrique qui régit le mouvement des électrons autour du noyau.

- À l'échelle astronomique, c'est l'interaction gravitationnelle qui régit les mouvements des satellites et des planètes.

Limites de la mécanique de Newton

Les interactions gravitationnelle et électrostatique sont régies par des lois qui s'expriment par le même formalisme (forces en $\left.1 / r^2\right)$

C'est sur cette base qu'Emest RUTHERFORD [1871-1937] (prix Nobel de chimie en 1908) élabore, en 1911, le modèle planétaire de l'atome : « Les électrons tournent autour du noyau comme les planètes autour du Soleil ».

- Tous les atomes d'un même élément ont le même rayon atomique, alors que l'on peut placer un satellite à n'importe quelle altitude autour de la Planète.

- L'énergie d'un système {Planète, satellite} peut varier continûment, alors que l'énergie d'un système {atome, électron} ne peut pas varier continûment : elle ne peut prendre que certaines valeurs discrètes, bien définies.

• Le modèle planétaire de l'atome n'est pas satisfaisant.
• La mécanique de Newton n'est pas applicable à l'échelle atomique.

Quantification des échanges d'énergie

Interaction d'un faisceau d'électrons avec la matière

Expérience

- Certains électrons ont perdu de l'énergie, qui a été transférée aux atomes de gaz.
- Ces pertes ne se font que par « paquets » appelés quanta d'énergie (quantum au singulier).
- Les atomes ne peuvent absorber que des quanta d'énergie

Conclusion

L'énergie d'un atome ne peut prendre que certaines valeurs discrètes formant une suite discontinue (appelées niveaux d'énergie).

L'énergie d'un atome est quantifiée, ses variations sont de l'ordre de l'électronvolt (eV).

[«Valeurs discrètes » veut dire l'opposé de «valeurs continues »]

Le modèle du photon

- L'interaction entre un atome et la lumière s'accompagne d'un échange énergétique.

L'énergie échangée est quantifiée. Donc, comme les électrons, la lumière transporte elle aussi de l'énergie.

- Dès 1900, Max Planck postule que la lumière transporte de l'énergie par quanta d'énergie.

- En 1905, Albert Einstein postule que ces quanta d'énergie sont portés par des particules de masse nulle, qu'il appelle photons.

- Une onde électromagnétique monochromatique, de fréquence $v$ et de longueur d'onde dans le vide $\lambda$, est constituée de photons. L'énergie d'un photon est : $\mathrm{E}=\mathrm{h} \cdot \mathrm{v}=\mathrm{h} \cdot \frac{\mathrm{c}}{\lambda}$.

$\mathrm{h}=6,63 \cdot 10^{-34} \mathrm{~J} \cdot \mathrm{s}$ est la constante de Planck.

Les postulats de BOHR

En 1913, Niels Bohr postule que :

• Les variations d'énergie de l'atome sont quantifiées.
• L'atome ne peut exister que dans certains états d'énergie bien définis ; chaque état est caractérisé par un niveau d'énergie.
• Un photon de fréquence $v$ est émis lorsque l'atome se désexcite en effectuant une transition d'un niveau d'énergie $E_p$ vers un niveau inférieur $E_n$ :

$E_p-E_n=h \cdot v$ (énergie du photon émis)

De même un atome passe d'un niveau d'énergie $E_n$ vers un niveau supérieur $E_p$ en absorbant un photon :

$\mathrm{E}_{\mathrm{p}}-\mathrm{E}_{\mathrm{n}}=\mathrm{h} \cdot v$ (énergie du photon absorbé)

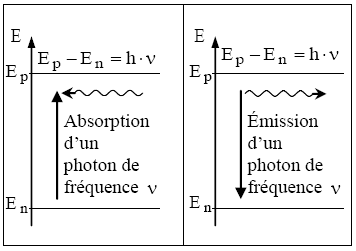
Quantification des niveaux d'énergie

لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

النسخة المجانية لكيزاكو:

• ملخصات الدروس غير محدودة
• فيديو مجاني في كل درس
• تمرين مصحح مجاني
• اختبار تفاعلي

إنشاء حساب مجاني