Travail de la force exercée par un opérateur sur un ressort
$\overrightarrow{\mathrm{F}_{\mathrm{Op}}}$ : force exercée par un opérateur lorsqu'il tire sur l'extrémité libre $\mathrm{M}$ d'un ressort pour la déplacer de $\mathrm{O}$ jusqu'à $\mathrm{B}$.
$3^{\text {ème }}$ loi de Newton : $\overrightarrow{F_{\mathrm{Op}}}=-\overrightarrow{\mathrm{F}}=\mathrm{k} \cdot \mathrm{x} \cdot \overrightarrow{\mathrm{i}}$
Travail élémentaire fournie par l'opérateur :
$$\delta \mathrm{W}=\overrightarrow{\mathrm{F}_{\mathrm{Op}}} \cdot \overrightarrow{\mathrm{d} \ell}=\mathrm{k} \cdot \mathrm{x} \cdot \overrightarrow{\mathrm{i}} \cdot \mathrm{dx} \cdot \overrightarrow{\mathrm{i}}=\mathrm{k} \cdot \mathrm{x} \cdot \mathrm{dx}$$
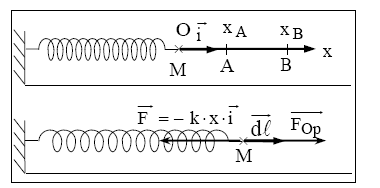
Le travail total lorsque M passe de A en B :
$$\mathrm{W}\left(\overrightarrow{\mathrm{F}_{\mathrm{Op}}}\right)=\int_{\mathrm{x}_{\mathrm{A}}}^{\mathrm{x} \mathrm{B}} \mathrm{k} \cdot \mathrm{x} \cdot \mathrm{dx}=\left[\frac{1}{2} \mathrm{k} \cdot \mathrm{x}^2\right]_{\mathrm{x} A}^{\mathrm{x} B}=\frac{1}{2}\left(\mathrm{k} \cdot \mathrm{x}_{\mathrm{B}}^2-\mathrm{k} \cdot \mathrm{x}_{\mathrm{A}}^2\right)$$
On retrouve ce résultat par une méthode graphique : le travail élémentaire est représenté par l'air d'un rectangle de longueur $\mathrm{k} \cdot \mathrm{x}$ et de largeur $\mathrm{dx}$.
Le travail total est égal à l'aire du trapèze rectangle $\mathrm{ABCD}$
$\mathrm{W}\left(\overrightarrow{\mathrm{F}_{\mathrm{Op}}}\right)=\mathrm{A}_{\mathrm{ABCD}}=\frac{1}{2}\left(\mathrm{k} \cdot \mathrm{x}_{\mathrm{B}}^2-\mathrm{k} \cdot \mathrm{x}_{\mathrm{A}}^2\right)$
$\mathrm{W}(\overrightarrow{\mathrm{F}})=-\mathrm{W}\left(\overrightarrow{\mathrm{F}_{\mathrm{Op}}}\right)=\frac{1}{2} \mathrm{x}_{\mathrm{A}}^2-\frac{1}{2} \mathrm{x}_{\mathrm{B}}^2$
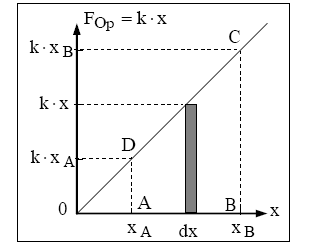
Étude énergétique du système $\{$ solide, ressort $\}$ horizontal
Énergie potentielle élastique
Théorème de l'énergie cinétique entre $\mathrm{G}_1$ et $\mathrm{G}_2$ :
$\Delta \mathrm{E}_{\mathrm{c}}\left(\mathrm{G}_1, \mathrm{G}_2\right)=\mathrm{W}(\overrightarrow{\mathrm{F}})+\mathrm{W}(\overrightarrow{\mathrm{P}})+\mathrm{W}(\overrightarrow{\mathrm{R}})$
$=\mathrm{W}(\overrightarrow{\mathrm{F}})$
$=\frac{1}{2} \mathrm{k} \cdot \mathrm{x}_1^2-\frac{1}{2} \mathrm{k} \cdot \mathrm{x}_2^2$
$=\left(\frac{1}{2} \mathrm{k} \cdot \mathrm{x}_1^2+\mathrm{C}\right)-\left(\frac{1}{2} \mathrm{k} \cdot \mathrm{x}_2^2+\mathrm{C}\right)$
$=E_{p e_1}-E_{p_2}$
$=-\Delta \mathrm{E}_{\mathrm{pe}}$
$\mathrm{L}$ 'expression $\mathrm{E}_{\mathrm{pe}}(\mathrm{x})=\frac{1}{2} \mathrm{k} \cdot \mathrm{x}^2+\mathrm{C}$ représente l'énergie potentielle élastique du ressort horizontal.
Un ressort allongé ou comprimé possède de l'énergie potentielle élastique en réserve, due à sa déformation. Il la restitue quand il reprend sa forme initiale.
Pour déterminer $\mathrm{C}$ on choisit un état de référence, $\Delta \ell_0=\mathrm{x}_{\mathrm{o}}$, dans lequel on accorde à $\mathrm{E}_{\text {pe }}$ la valeur nulle:
$$\mathrm{E}_{\mathrm{pe}}\left(\mathrm{x}_{\mathrm{o}}\right)=0 \Rightarrow \mathrm{C}=-\frac{1}{2} \mathrm{k} \cdot \mathrm{x}_{\mathrm{o}}^2$$
En pratique, la constante d'intégration est choisie de sorte que $\mathrm{E}_{\text {pe }}$ d'un ressort non déformé, soit nulle : $\mathrm{x}_0=0 \Rightarrow \mathrm{C}=0$
La variation de l'énergie potentielle élastique est égale à l'opposé du travail de la force de rappel : $\Delta \mathrm{E}_{\text {pe }}=-\mathrm{W}(\overrightarrow{\mathrm{F}})$
Énergie mécanique
L'énergie mécanique d'un système, à un instant t, dans un repère donné, est la somme de son énergie cinétique et de son énergie potentielle à cet instant.
$$\mathrm{E}_{\mathrm{m}}=\mathrm{E}_{\mathrm{c}}+\mathrm{E}_{\mathrm{p}}$$
- On choisit comme état de référence pour l'énergie potentielle de pesanteur le plan horizontal passant par $G$ : $E_{p p}=c t e=0$
- On choisit comme état de référence pour l'énergie potentielle élastique l'état où le ressort n'est pas déformé : C $=0$
$$\mathrm{E}_{\mathrm{m}}=\mathrm{E}_{\mathrm{c}}+\mathrm{E}_{\mathrm{pp}}+\mathrm{E}_{\mathrm{pe}}=\frac{1}{2} \mathrm{~m} \cdot \mathrm{v}^2+\frac{1}{2} \mathrm{k} \cdot \mathrm{x}^2$$
Cas d'un oscillateur non amorti
$x=x_m \cdot \cos \left(\frac{2 \pi}{T_0} \cdot t+\varphi\right) \Rightarrow v=-\frac{2 \pi}{T_0} \cdot x_m \cdot \sin \left(\frac{2 \pi}{T_0} \cdot t+\varphi\right)=-v_m \cdot \sin \left(\frac{2 \pi}{T_0} \cdot t+\varphi\right)$
$\mathrm{v}_{\mathrm{m}}=\frac{2 \pi}{\mathrm{T}_{\mathrm{o}}} \cdot \mathrm{x}_{\mathrm{m}}=\sqrt{\frac{\mathrm{k}}{\mathrm{m}}} \cdot \mathrm{x}_{\mathrm{m}} \Rightarrow \mathrm{m} \cdot \mathrm{v}_{\mathrm{m}}^2=\mathrm{k} \cdot \mathrm{x}_{\mathrm{m}}^2$
$\mathrm{E}_{\mathrm{m}}=\frac{1}{2} \mathrm{~m} \cdot\left[\sqrt{\frac{\mathrm{k}}{\mathrm{m}}} \cdot \mathrm{x}_{\mathrm{m}} \cdot \sin \left(\frac{2 \pi}{\mathrm{T}_{\mathrm{o}}} \cdot \mathrm{t}+\varphi\right)\right]^2+\frac{1}{2} \mathrm{k} \cdot\left[\mathrm{x}_{\mathrm{m}} \cdot \cos \left(\frac{2 \pi}{\mathrm{T}_{\mathrm{o}}} \cdot \mathrm{t}+\varphi\right)\right]^2$
$=\frac{1}{2} \mathrm{k} \cdot \mathrm{x}_{\mathrm{m}}^2 \cdot\left[\sin ^2\left(\frac{2 \pi}{\mathrm{T}_{\mathrm{o}}} \cdot \mathrm{t}+\varphi\right)+\cos ^2\left(\frac{2 \pi}{\mathrm{T}_{\mathrm{o}}} \cdot \mathrm{t}+\varphi\right)\right]$
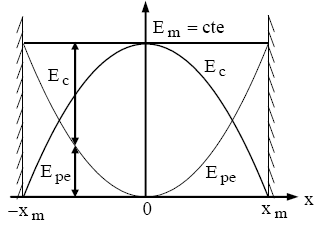
$=\frac{1}{2} \mathrm{k} \cdot \mathrm{x}_{\mathrm{m}}^2=\mathrm{E}_{\text {pemax }}$
$=\frac{1}{2} \mathrm{~m} \cdot \mathrm{v}_{\mathrm{m}}^2=\mathrm{E}_{\mathrm{c} \max }$
En l'absence de frottement, l'énergie mécanique se conserve.
La force de rappel $\overrightarrow{\mathrm{F}}$ est dite conservative.
$\mathrm{E}_{\mathrm{m}}=\mathrm{E}_{\mathrm{c}}+\mathrm{E}_{\mathrm{pe}}=\mathrm{cte} \Rightarrow \Delta \mathrm{E}_{\mathrm{m}}=\Delta \mathrm{E}_{\mathrm{c}}+\Delta \mathrm{E}_{\mathrm{pe}}=0 \Rightarrow \Delta \mathrm{E}_{\mathrm{c}}=-\Delta \mathrm{E}_{\mathrm{pe}}$
Il y a transformation entre les énergies cinétique et potentielle élastique.
Remarque
établissement de l'équation différentielle
$\mathrm{E}_{\mathrm{m}}=\frac{1}{2} \mathrm{~m} \cdot \dot{\mathrm{x}}^2+\frac{1}{2} \mathrm{k} \cdot \mathrm{x}^2=\mathrm{cte}$
$\Rightarrow \frac{\mathrm{dE}_{\mathrm{m}}}{\mathrm{dt}}=\frac{1}{2} \mathrm{~m} \cdot(2 \ddot{\mathrm{x}} \cdot \dot{\mathrm{x}})+\frac{1}{2} \mathrm{k} \cdot(2 \dot{\mathrm{x}} \cdot \mathrm{x})=(\mathrm{m} \cdot \ddot{\mathrm{x}}+\mathrm{k} \cdot \mathrm{x}) \cdot \dot{\mathrm{x}}=0$
$\Rightarrow \quad \mathrm{m} \cdot \ddot{\mathrm{x}}+\mathrm{k} \cdot \mathrm{x}=0$
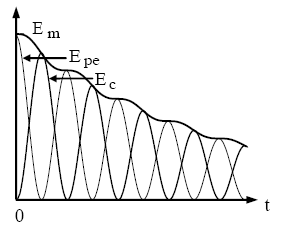
Cas d'un oscillateur amorti
À cause des frottements, l'énergie mécanique diminue : les forces de frottement sont dites non conservatives.
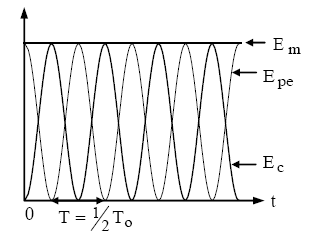
Oscillateur non amorti.
Représentation de $E_{\text {pe }}$ et $E_c$
en fonction de $t$
Oscillateur non amorti.
Représentation de $E_{p e}$ et $E_c$
en fonction de $x$
Oscillateur non amorti.
Représentation de $E_{p e}$ et $E_c$
en fonction de $t$
Étude énergétique du pendule de torsion
لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

- ملخصات الدروس غير محدودة
- فيديو مجاني في كل درس
- تمرين مصحح مجاني
- اختبار تفاعلي