Le mouvement

Repérage dans l'espace

L'étude de la mécanique est, pour un physicien, l'étude des mouvements : leur description, leurs causes, leurs effets, leurs empêchements...Comment s'y prendre pour étudier un mouvement ? Qu'évoque pour vous le mot mouvement : déplacement, trajectoire, vitesse, durée ? il manque à cette liste un mot clé.

Pour mieux le saisir, fermons les yeux un instant et imaginons un cosmonaute en train de voguer dans les espaces intersidéraux. Autour de lui, tout est noir. Il est inquiet. II ne sait pas si sa cabine spatiale continue à se déplacer. Voilà un autre vaisseau qui s'approche. II va enfin savoir. Le vaisseau le dépasse. Mais est-ce son véhicule qui recule, ou L'autre qui avance ? à quelle distance du soleil se trouve-t-il ? Comment faire pour connaitre sa vitesse ? il n'a plus de montre, et pour lui il n'y a plus de jour ni de nuit. Dans combien de temps arrivera-t-il ? Quel est donc ce mot-clé qui manque ? Vous  l'avez probablement trouvé : c'est le repère. On ne peut pas étudier un mouvement sans avoir défini un repère, et même deux repères : un repère d'espace et un repère de temps

doc1

Repérage cartésiens

 Pour déterminer la position dans l'espace d'un mobile, nous utilisons plusieurs types de repères dont :

Repérage cartésiens

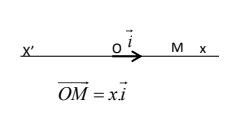
Doc 2

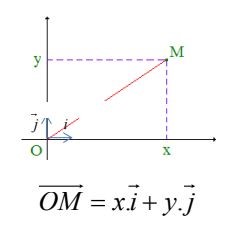
Doc 3

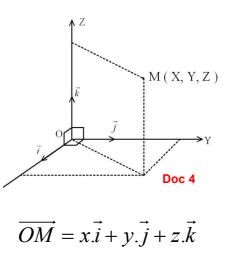
Repérer la position d'un point dans l'espace revient à évaluer des distances et des écarts angulaires. Pour ce faire, il est nécessaire de choisir des unités d'angles, de longueur et de disposer d'appareils de mesure appropriés

Repérage non cartésien

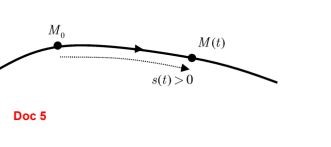
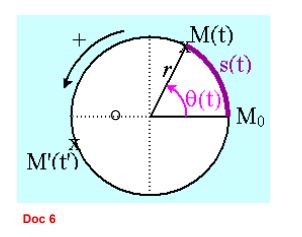
Lors d'un mouvement de trajectoire quelconque, nous repérons la position d'un point du mobile par la distance : $$\mathbf{s}=\mathbf{M}_{0} \mathbf{M}$$. $\mathbf{s}$ représente la longueur de l'arc $$\mathrm{M}_{0} \mathrm{M}$$ appelée abscisse curviligne.

Dans le cas d'un mouvement circulaire, la position d'un point du mobile est repérée par l'angle $$\theta$$ appelé : abscisse curviligne après choix d'un sens de rotation.

$$\boldsymbol{\Theta}=\left(\mathrm{OM}, \mathrm{OM}_{0}\right)$$

Repérage dans le temps

Origine des dates

Nous avons tous - sans que cela soit nécessaire - La notion intuitive du temps qui s'écoule irréversiblement, du passé vers l'avenir en passant par le présent.

A chaque instant, nous associons un nombre réel appelé la date. L'origine des temps correspond à la date $$t=0$$. Cette origine est choisie arbitrairement, suivant votre convenance.

Mesure de la durée

On appelle durée $\Delta t$ l'intervalle de temps séparant deux dates $$t _{2}$$ et $$t_{1}$$, soit : $$\Delta t=t_{2}-_{1}$$

Trajectoire d'un mobile

Doc 8. Chronophotographie de la trajectoire d'un skieur

Caractère relatif du mouvement

لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو

النسخة المجانية لكيزاكو:

• ملخصات الدروس غير محدودة
• فيديو مجاني في كل درس
• تمرين مصحح مجاني
• اختبار تفاعلي

إنشاء حساب مجاني