-
-
Maths
Les polynômes
Tronc Commun Scientifique Maths Les polynômes fiche de cours
Introduction et égalité de deux polynômes
Introduction
Activité
Soit un parallélépipède rectangle dont les dimensions sont $$x$$ , $$x+1$$ et $$x-2$$ avec $$x$$ un réel strictement positif. Soit $$V(x)$$ le volume de ce parallélépipède.
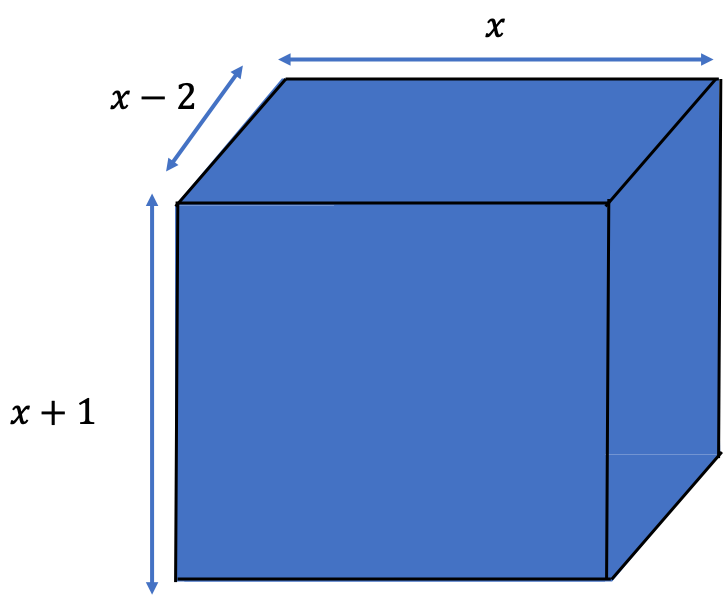
1) Calculer $$V(x)$$ en fonction de $$x$$.
2) Calculer $$V(3)$$ et $$V(4)$$.
Réponse :
1) Le volume du parallélépipède $$V(x) = x.(x-2).(x+1)=(x^2-2x)(x+1)$$ = $$x^3+x^2-2x^2-2x$$
Donc $$V(x) = x^3 - x^2 - 2x $$.
2) $$V(3) = 12$$ et $$V(4)=40$$
Vocabulaire
- L'expression $$V(x) = x^3 - x^2 - 2x $$ est appelée polynôme de degré 3.
- Généralement, on note les polynômes $$P(x)$$ , $$Q(x)$$ ou $$R(x)$$.....
- La notation du degré est la suivante $$d°(V)=3$$
- Les nombres $$1$$,$$-1$$ et $$-2$$ sont appelés coefficients du polynôme.
Définition
تعريف
Soit $$x$$ une variable de $$\mathbb{R}$$ et $$n$$ de $$\mathbb{N^*}$$
Soient $$a_0$$, $$a_1$$......, $$a_n$$ des réels tels quel $$a_n \neq 0$$
- L'expression $$a_0 + a_1x + .......a_{n-1}x^{n-1} + a_nx^n$$ est appelée polynôme de degré $$n$$ ( écrit dans le sens croissant).
- L'expression $$a_nx^n+a_{n-1}x^{n-1} + ....... + a_1x + a_0$$ est appelée polynôme de degré $$n$$ ( écrit dans le sens croissant).
- Chaque terme de cette somme est appelé monôme ( exemple $$a_0$$ est un monôme de degré $$0$$ et $$a_2x^2$$ est un monôme de degré $$2$$).
- Les polynômes sont généralement notés $$P(x)$$ , $$Q(x)$$....
- Le degré d'un polynôme est noté $$d°(P)=n$$
- Les réels $$a_0$$, $$a_1$$......, $$a_n$$ sont appelés coefficients du polynôme.
- Si $$P(x)=a_0$$ avec $$a_0 \neq 0$$ alors $$d°(P)=0$$
- Si $$a_0$$, $$a_1$$......, $$a_n$$ sont tous nuls, alors $$P(x)=0$$ et il n'admet pas de degré.
Cas particuliers :
- L'expression $$ax$$ avec $$a \neq 0$$ est appelé monôme de degré $$1$$.
- L'expression $$ax^2$$ avec $$a \neq 0$$ est appelé monôme de degré $$2$$.
- L'expression $$ax+b$$ avec $$a \neq 0$$ est appelé binôme de degré $$1$$.
- L'expression $$ax^2+bx+c$$ avec $$a \neq 0$$ est appelé trinôme de degré $$2$$.
Egalité de deux polynômes
Activité
On considère le polynôme $$P(x) = 3x^3 - 2x^2-x+2$$ et $$Q(x)=ax^3 +(b-1)x^2+2cx+d$$
- Déterminer $$a$$, $$b$$ , $$c$$ et $$d$$ tels que $$P(x) = Q(x)$$.
- Donner la propriété.
Réponse :
$$P(x)=Q(x)$$ signifie que pour tout réel $$x$$ : $$3x^3 - 2x^2-x+2 = ax^3 +(b-1)x^2+2cx+d$$.
Nous obtenons alors $$3x^3 - 2x^2-x+2 - ( ax^3 +(b-1)x^2+2cx+d ) = 0$$ pour tout réel $$x$$.
Ce qui veut dire : $$(3-a)x^3+(-b+1 - 2)x^2-(2c+1)x+2 -d = 0$$ pour tout réel $$x$$.
C'est à dire : $$(3-a)x^3-(b+1)x^2-(2c+1)x+(2 -d) = 0$$ pour tout réel $$x$$.
Cette égalité est valable pour tout réel $$x$$.
Pour $$x=0$$, nous obtenons : $$2-d=0$$ donc $$d=2$$.
ainsi : $$(3-a)x^3-(b+1)x^2-(2c+1)x = 0$$ pour tout réel $$x$$.
Factorisons : $$ x ( (3-a)x^2 -(b+1)x - (2c+1) ) = 0 $$ pour tout réel $$x$$.
donc pour tout réel $$x$$ non nul : $$(3-a)x^2 -(b+1)x - (2c+1) = 0$$
prenons respectivement $$x=1$$, $$x=-1$$ et $$x=2$$.
Nous avons :
$$ -a -b - 2c+1 = 0$$ $$(1)$$
$$-a+b-2c+3= 0$$ $$(2)$$
$$-4a-2b-2c+9=0$$ $$(3)$$
$$(2)-(1)$$ donne : $$ 2b+2=0$$ donc $$b=-1$$.
On injecte $$b=-1$$ dans $$(2)$$ : $$-a+2-2c=0$$ ce qui donne $$a=2-2c$$.
On injecte dans $$(3)$$ : $$-4(2-2c)+2-2c+9=0$$
Nous obtenons donc : $$6c-3=0$$ donc $$c=\frac{1}{2}$$
Finalement on trouve que $$a=3$$.
2) On remarque que les coefficients de $$P(x)$$ et $$Q(x)$$ sont deux à deux égaux !
خاصية
$$P(x)$$ et $$Q(x)$$ sont deux polynômes égaux si et seulement si :
- Ils ont le même degré
- Les coefficients des monômes du même degré sont égaux
تطبيق
Soit $$P(x)$$ un polynôme du 3ème degré tel que P(1)=P(-1) = 0.
$$P(x)$$ et le polynôme $$2x^2-x+1$$ ont le même coefficient pour leurs monômes du deuxième degré.
Réponse :
$$P(x)$$ et le polynôme $$2x^2-x+1$$ ont le même coefficient pour leurs monômes du deuxième degré signifie que l'on peut écrire $$P(x) = 2x^2 +bx + c$$ avec $$b$$ et $$c$$ deux réels.
$$P(1)=0$$ donne : $$2+b+c = 0$$ $$(1)$$
$$P(-1)=0$$ donne : $$2-b+c=0$$ $$(2)$$
$$(1)+(2)$$ donne : $$ 2c+4=0$$ donc : $$c=-2$$.
Finalement on trouve que $$b=0$$
Donc $$P(x) = 2x^2-2$$
La somme et le produit de deux polynômes
لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو
- ملخصات الدروس غير محدودة
- فيديو مجاني في كل درس
- تمرين مصحح مجاني
- اختبار تفاعلي
Signaler une erreur